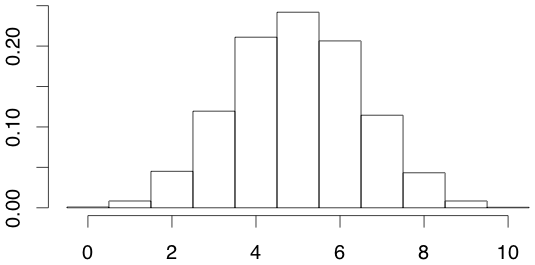
- 表が出にくいのではないか(作業仮説)
- 表は 5 回くらいは出そう
- 表が一回以下しか出ないのは 0.011
- 裏が一回以下しか出ないのは 0.011
↓
こんなことは「よく起きること」なのだ
医用統計学入門
統計学の概念とよく使われる手法の解説
検定の考え方 ★
実例


検定の流れ
帰無仮説・対立仮説
数学の「証明」との違い
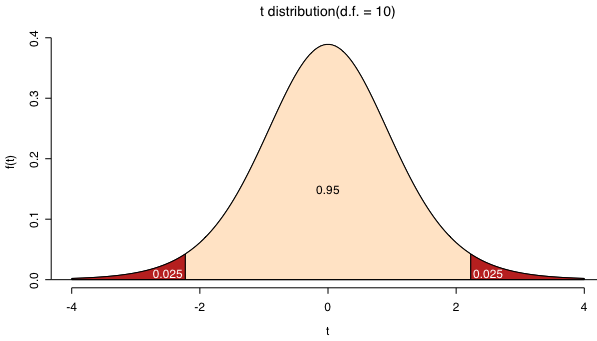
片側検定と両側検定
検定法の選択
検定統計量
P値(有意確率)
 |  |
第一種の過誤(αエラー)
帰無仮説が正しいときに,帰無仮説が誤りであるとして棄却するという誤り
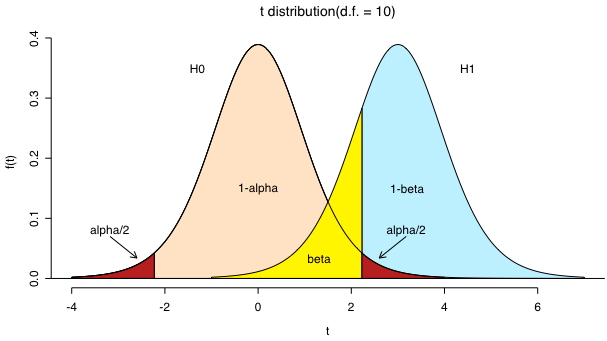
有意水準の設定
検定による意思決定
第二種の過誤(βエラー)
帰無仮説が誤っているにもかかわらず,帰無仮説を棄却できないという誤り
検出力(1−β)
対立仮説が正しいときに,帰無仮説を棄却して対立仮説を採択できる確率(β=4α 程度が望ましい?)
まとめると
| 検定の結果 | |||
|---|---|---|---|
| 帰無仮説を棄却できない | 帰無仮説を棄却する | ||
| 真実 | 帰無仮説が正しい | 正しい決定 | あわてん坊のエラー α |
| 帰無仮説は誤り | ボンヤリ者のエラー β | 正しい決定 1−β | |
注意すべきこと
検定結果の取り扱い
| 検定の結果 | ||
|---|---|---|
| 統計学的に有意だった | 統計学的に有意でなかった | |
| 実質的な意味がある | 得られた知見を堂々と発表する | もう少しデータを蓄積する データの精度を上げる |
| 実質的な意味がない | 検定は不要だった | 検定は不要だった |
代表的な検定
検定のマニュアル
独立性の検定
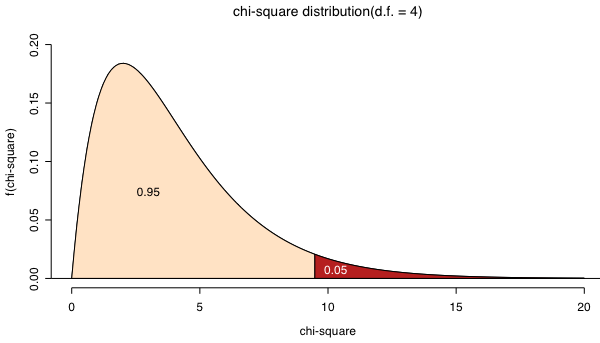
カイ二乗検定
> chisq.test(matrix(c(16,12,15,9,12,5,11,2,36,20,24,1),nrow=4)) Pearson's Chi-squared test data: matrix(c(16, 12, 15, 9, 12, 5, 11, 2, 36, 20, 24, 1), nrow = 4) X-squared = 13.7134, df = 6, p-value = 0.03301 Warning message: Chi-squared approximation may be incorrect in: chisq.test(matrix(c(16, 12, 15, 9, 12, 5, 11, 2, 36, 20, 24, > chisq.test(matrix(c(40,10,20,60),nrow=2),correct=FALSE) Pearson's Chi-squared test data: matrix(c(40, 10, 20, 60), nrow = 2) X-squared = 37.4524, df = 1, p-value = 9.367e-10
フィッシャーの正確検定
> fisher.test(matrix(c(4,1,2,6),nrow=2)) Fisher's Exact Test for Count Data data: matrix(c(4, 1, 2, 6), nrow = 2) p-value = 0.1026 alternative hypothesis: true odds ratio is not equal to 1 95 percent confidence interval: 0.5364938 682.2665965 sample estimates: odds ratio 9.47099 > fisher.test(matrix(c(16,12,15,9,12,5,11,2,36,20,24,1),nrow=4)) Fisher's Exact Test for Count Data data: matrix(c(16, 12, 15, 9, 12, 5, 11, 2, 36, 20, 24, 1), nrow = 4) p-value = 0.03447 alternative hypothesis: two.sided
2 個の代表値の差の検定
代表値とは
対応のあるデータとは
平均値の差の検定
いわゆる t 検定
> my.t.test <- function(n1, x1, u1, n2, x2, u2, welch = FALSE) + { + method <- paste(if (!welch) "Welch", "Two Sample t-test") + if (welch) { + df <- n1+n2-2 + v <- ((n1-1)*u1+(n2-1)*u2)/df + tstat <- abs(x1-x2)/sqrt(v*(1/n1+1/n2)) + } + else { + tstat <- abs(x1-x2)/sqrt(u1/n1+u2/n2) + df <- (u1/n1+u2/n2)^2/((u1/n1)^2/(n1-1)+(u2/n2)^2/(n2-1)) + } + pval <- 2*pt(-tstat, df) + result <- c(tstat, df, pval) + names(result) <- c("t value", "d. f.", "P value") + return(list(method=method, result=result)) + } > my.t.test(36, 82.6, 15.3, 43, 84.5, 16.2, welch=TRUE) $method [1] "Two Sample t-test" $result t value d. f. P value 2.11651800 77.00000000 0.03753134 > my.t.test(36, 82.6, 15.3, 43, 84.5, 16.2, welch=FALSE) $method [1] "Welch Two Sample t-test" $result t value d. f. P value 2.12195266 75.26729060 0.03713237
> first <- c(7,11,10,10,13,10,9,8,11,12,6,13,11,8,11) > second <- c(4,9,7,6,10,12,10,5,12,10,5,10,15,9,9) > t.test(first, second, paired=TRUE) Paired t-test data: first and second t = 1.8628, df = 14, p-value = 0.0836 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.1715693 2.4382360 sample estimates: mean of the differences 1.133333
代表値の差の検定
> gr1 <- c(78,64,75,45,82) > gr2 <- c(110,70,53,51) > wilcox.test(gr1, gr2) Wilcoxon rank sum test data: gr1 and gr2 W = 11, p-value = 0.9048 alternative hypothesis: true mu is not equal to 0
> x <- c(269,230,365,282,295,212,346,207,308,257) > y <- c(273,213,383,282,297,213,351,208,294,238) > wilcox.test(x, y, paired=TRUE,correct=FALSE) Wilcoxon signed rank test data: x and y V = 22, p-value = 0.9527 alternative hypothesis: true mu is not equal to 0 Warning messages: 1: Cannot compute exact p-value with ties in: wilcox.test.default(x, y, paired = TRUE, correct = FALSE) 2: Cannot compute exact p-value with zeroes in: wilcox.test.default(x, y, paired = TRUE, correct = FALSE)
生存率解析
方法
> group <- c(1, 1, 2, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 1, 2, 2, 2, 1, 1, 2, 1, 2, 1, 2, 1, 2, 2, 1, 1, 1) > event <- c(1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0) > time <- c(2, 20, 5, 1, 3, 17, 2, 3, 15, 14, 12, 13, 11, 11, 10, 8, 8, 3, 7, 3, 6, 2, 5, 4, 2, 3, 1, 3, 2, 1) > a.group <- group == 1 > km.surv(time[a.group], event[a.group]) i time truncate p P SE [1,] 1 1 1 1.0000000 1.0000000 NA [2,] 2 2 0 0.9333333 0.9333333 0.06440612 [3,] 3 2 0 0.9285714 0.8666667 0.08777075 [4,] 4 2 1 1.0000000 0.8666667 NA [5,] 5 3 1 1.0000000 0.8666667 NA [6,] 6 3 1 1.0000000 0.8666667 NA [7,] 7 3 1 1.0000000 0.8666667 NA [8,] 8 5 1 1.0000000 0.8666667 NA [9,] 9 6 1 1.0000000 0.8666667 NA [10,] 10 7 0 0.8571429 0.7428571 0.13710884 [11,] 11 11 1 1.0000000 0.7428571 NA [12,] 12 11 1 1.0000000 0.7428571 NA [13,] 13 13 0 0.7500000 0.5571429 0.19089707 [14,] 14 15 1 1.0000000 0.5571429 NA [15,] 15 17 1 1.0000000 0.5571429 NA [16,] 16 20 1 1.0000000 0.5571429 NA > library(survival) > dat <- Surv(time[a.group], event[a.group]) > res <- survfit(dat) > res Call: survfit(formula = dat) n events rmean se(rmean) median 0.95LCL 0.95UCL 16.00 4.00 14.69 2.14 Inf 13.00 Inf > summary(res) Call: survfit(formula = dat) time n.risk n.event survival std.err lower 95% CI upper 95% CI 2 15 2 0.867 0.0878 0.711 1 7 7 1 0.743 0.1371 0.517 1 13 4 1 0.557 0.1909 0.285 1 > plot(res)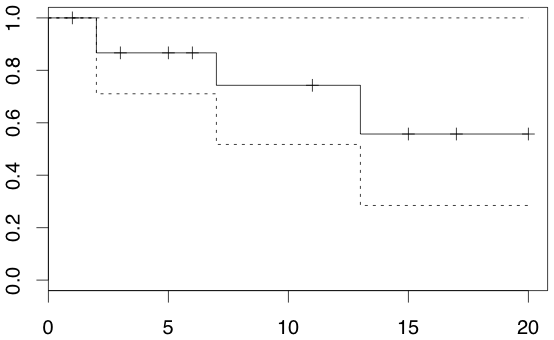
生存率の検定
Cox の比例ハザードモデル ★
時間に関係なく,二群のハザード比(瞬間死亡率の比)が一定であると仮定したモデル
上の結果の解釈> library(eha) > dat <- data.frame(time = c(4, 3, 1, 1, 2, 2, 3), status = c(1, 1, 1, 0, 1, 1, 0), x = c(0, 2, 1, 1, 1, 0, 0), sex = c(0, 0, 0, 0, 1, 1, 1)) > coxreg(Surv(time, status) ~ x + strata(sex), data = dat) Call: coxreg(formula = Surv(time, status) ~ x + strata(sex), data = dat) Covariate Mean Coef Rel.Risk L-R p Wald p x 0.625 0.802 2.231 0.329 Events 5 Total time at risk 16 Max. log. likelihood -3.3277 LR test statistic 1.09 Degrees of freedom 1 Overall p-value 0.297117
クラスター分析 ★
クラスター分析の手順
クラスター分析の手法
| ウォード法 | 最も明確なクラスターを作る |
| 最近隣法 | 分類感度は低い |
| 最遠隣法 | 分類感度は高い |
| メディアン法 | 最近隣法と最遠隣法の折衷 |
| メディアン法 重心法 | 距離の逆転が生じることがある |
| 可変法 | パラメータの設定による |
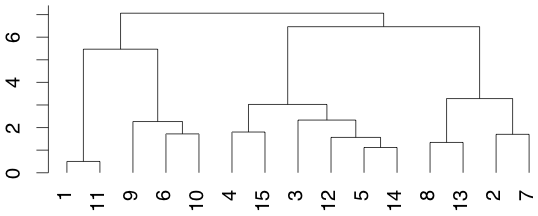
> data <- matrix(c( + 10.2, 6.3, + 1.7, 7.8, + 0.6, 0.1, + 3.0, 2.5, + 2.1, 0.0, + 7.7, 2.2, + 3.2, 8.6, + 4.9, 7.2, + 9.1, 0.6, + 6.7, 0.8, + 9.9, 5.9, + 3.8, 0.9, + 5.5, 6.0, + 2.6, 1.0, + 2.0, 4.0 + ), byrow=TRUE, nc=2) > plot(data) > text(data, offset=0.2,pos=4) > plot(hclust(dist(data), "average"), hang=-1)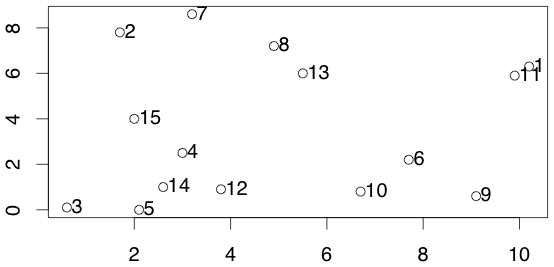
k-means 法
> library(mva) Warning message: package 'mva' has been merged into 'stats' (R.1.9.0 から) > x <- matrix(c( + -0.639, -0.242, + 1.320, 0.519, + 0.775, -1.996, + 0.126, 0.728, + 1.117, 1.576, + -1.809, 0.595, + -0.016, -0.871, + -0.319, -0.280, + -1.438, 0.583, + -0.233, 0.905 + ), byrow=TRUE, ncol=2) > result <- kmeans(x, 3) > result $cluster [1] 3 1 3 1 1 2 3 3 2 1 $centers [,1] [,2] 1 0.58250 0.93200 2 -1.62350 0.58900 3 -0.04975 -0.84725 $withinss [1] 2.3306790 0.0688925 3.1093535 $size [1] 4 2 4 > plot(x, xlim=c(-2,2), ylim=c(-2,2)) > text(x[,1], x[,2], result$cluster, pos=4, offset=0.5)
URL など