分割表において，期待値が 5 以下の桝目が全体の桝目の 20% 以上あるか，期待値が 1 以下の桝目が 1 つでもある場合には，「$\chi^2$ 分布を利用する独立性の検定」は不適当である（注意事項，注意事項 2）。そのような場合には本法により独立性の検定を行う。
　注：多くの教科書には「フィッシャーの正確確率検定は $2 \times 2$ 分割表のときの検定法である」と書かれているが，それより大きい分割表の場合にも正確な $P$ 値を求めることができる。

例題：

　「表 1 のようなクロス集計表に基づき，“甘いものが好きか嫌いか”と“虫歯の有無”の間に関連があるか検定しなさい。」

　この問は，「甘いものが好きな群と嫌いな群で，虫歯の保有率に差があるか検定しなさい。」とも解釈できる。

検定手順：

1. 前提
   • 帰無仮説 $H_0$：「2 要因は独立である」，または「比率に差がない」。
   • 対立仮説 $H_1$：「2 要因は独立でない」，または「比率に差がある」。
   • 有意水準 $\alpha$ で両側検定を行う（片側検定も可能である）。

2. 2 変数 A，B についての分割表を表 2 のように定義する。
   2 群の比率の差の検定を行うと解釈する場合には要因 A（または要因 B）が群になる。

   表 2．$2 \times 2$ 分割表

   		要因 B
   		$B_{1}$	$B_{2}$	合計
   要因 A	$A_{1}$	$a$	$b$	$e$
   	$A_{2}$	$c$	$d$	$f$
   	合計	$g$	$h$	$n$

3. 周辺度数 $e$，$f$，$g$，$h$ を固定した分割表は複数個考えられるが，観察された分割表が得られる確率は次式のようになる。

   $P_{a} = \displaystyle \frac{{}_{e}C_{a} \times {}_{f}C_{c}} {{}_{n}C_{g}} = \frac{e!\ f!\ g!\ h!} {n!\ a!\ b!\ c!\ d!}$

   これを，例題で説明しよう。

   1. まず，“甘いものが好き”な $17$ 人から $13$ 人を取り出す取り出し方は，
      ${}_{17}C_{13} = 2380$ 通りある。

   2. 同様に，“甘いものが嫌い”な $20$ 人から $6$ 人を取り出す取り出し方は，
      ${}_{20}C_{6} = 38760$ 通りある。

   3. 帰無仮説が正しいとすると「“甘いものが好きか嫌いか”と“虫歯があるかないか”は“独立事象”なので，“甘いものが好き”な $17$ 人から $13$ 人，“甘いものが嫌い”な $20$ 人から $6$ 人を取り出す取り出し方は，
      ${}_{17}C_{13} \times _{20}C_{6} = 2380 \times 38760 = 92248800$ 通りあることになる。

   4. ここで，全体の人数 $37$ 人から $13 + 6 = 19$ 人を取り出す取り出し方は，
      ${}_{37}C_{19} = 17672631900$ 通りある。

   5. したがって，表 1 のような $2 \times 2$ 分割表の生起確率は，
      $P_{a} = \displaystyle \frac{{}_{17}C_{13} \times {}_{20}C_{6}} {{}_{37}C_{19}} = \frac{2380\times 38760}{17672631900} = 0.00522$
      であると計算できる。

4. 周辺度数を固定したとき，$2 \times 2$ 分割表の自由度は $1$ であり，4 つの桝目のどれか 1 つを決めれば，残りの桝目は自動的に決る。

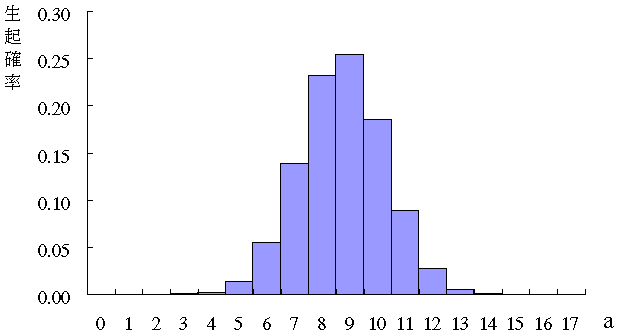
   例題では，$a$ をいろいろと変えることによって，表 3 のような分割表が得られる。

   表 3．周辺度数を固定したときの $2 \times 2$ 分割表

   虫歯 あり なし 合計 甘いもの 好き 0 17 17 嫌い 19 1 20 合計 19 18 37		左下からの続き ： ：
   虫歯 あり なし 合計 甘いもの 好き 1 16 17 嫌い 18 2 20 合計 19 18 37		虫歯 あり なし 合計 甘いもの 好き 15 2 17 嫌い 4 16 20 合計 19 18 37
   虫歯 あり なし 合計 甘いもの 好き 2 15 17 嫌い 17 3 20 合計 19 18 37		虫歯 あり なし 合計 甘いもの 好き 16 1 17 嫌い 3 17 20 合計 19 18 37
   ： ： 右上へ続く		虫歯 あり なし 合計 甘いもの 好き 17 0 17 嫌い 2 18 20 合計 19 18 37

5. 観察された $2 \times 2$ 分割表の生起確率を $P_{o}$ とする。

   例題では，$P_{o} = 0.005219867676$ である。

6. 表 3 のようなそれぞれの分割表が得られる確率 $P_{a}$ を計算する。
   また，2 要因の関連の強さの指標として，$a\ d - b\ c$ を定義し，それぞれに対応したものを $S_{a}$，$S_{o}$ とする。

   例題では，これらをまとめると，表 4 のようになる。

   表 4．分割表の生起確率

   $a$	$b$	$c$	$d$	$a\ d - b\ c$	分割表の生起確率	累積確率 1	累積確率 2
   0	17	19	1	$-$323	@ 0.000000001132	0.000000001132	1.000000000000
   1	16	18	2	$-$286	@ 0.000000182768	0.000000183900	0.999999998868
   2	15	17	3	$-$249	@ 0.000008772887	0.000008956787	0.999999816100
   3	14	16	4	$-$212	@ 0.000186423846	0.000195380633	0.999991043213
   4	13	15	5	$-$175	@ 0.002087947070	0.002283327703	0.999804619367
   5	12	14	6	$-$138	0.013571655957	0.015854983660	0.997716672297
   6	11	13	7	$-$101	0.054286623828	0.070141607487	0.984145016340
   7	10	12	8	$-$64	0.138624771560	0.208766379047	0.929858392513
   8	9	11	9	$-$27	0.231041285933	0.439807664981	0.791233620953
   9	8	10	10	10	0.254145414527	0.693953079507	0.560192335019
   10	7	9	11	47	0.184833028747	0.878786108254	0.306046920493
   11	6	8	12	84	0.088215763720	0.967001871974	0.121213891746
   12	5	7	13	121	0.027143311914	0.994145183887	0.032998128026
   13	4	6	14	158	@ 0.005219867676	0.999365051563	0.005854816113
   14	3	5	15	195	@ 0.000596556306	0.999961607869	0.000634948437
   15	2	4	16	232	@ 0.000037284769	0.999998892638	0.000038392131
   16	1	3	17	269	@ 0.000001096611	0.999999989249	0.000001107362
   17	0	2	18	306	@ 0.000000010751	1.000000000000	0.000000010751

   太字は観察された分割表。 @ は両側・片側検定での有意確率の計算に使われるもの。

7. 検定は，表 4 のような結果に基づいて以下のようにして行う。(注)
   1. 片側検定の場合
      1. 得られた分割表のうち，観察された分割表より極端な側の分割表（$S_{a}$，$S_{o}$ が同符号でかつ $|\ S_{a}\ | \geqq |\ S_{o}\ |$）の生起確率を合計したものを P とする。
      2. 帰無仮説の採否を決める。
         • $P \gt \alpha$ のとき，帰無仮説は棄却できない。「$2$ 要因は独立でないとはいえない」。
         • $P \leqq \alpha$ のとき，帰無仮説を棄却する。「$2$ 要因は独立ではない」。

      例題は両側検定を要求しているが，片側検定の場合について説明する。例題では，表 4 において，観察された表を含めてそれよりも極端な側の分割表は，$a = 13, 14, 15, 16, 17$ の $5$ つの表である。したがって，
      \[ \begin{align*} P &= P_{13} + P_{14} + P_{15} + P_{16} + P_{17}\\ &= 0.005219867676 + 0.000596556306 + 0.000037284769 + 0.000001096611 + 0.000000010751\\ 　&= 0.0058548 \end{align*} \] となり，帰無仮説は棄却される。

   2. 両側検定の場合
      1. 得られた分割表のうち，観察された分割表より極端な側の分割表（$|\ S_{a}\ | \geqq\ | S_{o}\ |$）の生起確率を合計したものを $P$ とする。
      2. 帰無仮説の採否を決める。
         • $P \gt \alpha$ のとき，帰無仮説は棄却できない。「$2$ 要因は独立でないとはいえない」。
         • $P \leqq \alpha$ のとき，帰無仮説を棄却する。「$2$ 要因は独立ではない」。

      例題では，表 4 において，観察された表を含めてそれよりも極端な側の分割表は，$a = 0, 1, 2, 3, 4, 13, 14, 15, 16, 17$ の $10$ 個の表である。したがって，
      \[ \begin{align*} P &= P + P_{1} + P_{2} + P_{3} + P_{4} + P_{13} + P_{14} + P_{15} + P_{16} + P_{17}\\ 　&= 0.000000001132 + 0.000000182768 + 0.000008772887 + 0.000186423846 + 0.002087947070\\ 　& + 0.005219867676+ 0.000596556306 + 0.000037284769 + 0.000001096611 + 0.000000010751\\ &= 0.0081381 \end{align*} \] となり，帰無仮説は棄却される。

注：$P$ 値を求めるためにここで示した方法は，Pearson のカイ二乗法と呼ばれるものである。この方法では，分割表において独立性の検定のためのカイ二乗統計量を計算し，その値が観察された分割表に対して計算されるものよりも大きい分割表を「極端な分割表」とするものである。上の計算では $a\ d-b\ c$ を計算しているが，これはカイ二乗統計量の構成要素である。
　Fisher が示した正確確率検定は，観察された分割表の生起確率よりも小さな生起確率を持つ分割表を「極端な分割表」であるとして，その生起確率を加えたものを $P$ 値とするものである。
　二つの方法による $P$ 値は多くの場合には一致するが，異なることもある。

R で計算してみる

いくつかの注意点

演習問題：

　「13 人の学生について，自動車運転免許を持っているかどうかを調査した結果が，表 5 のようにまとめられた。男女で免許保有率に差があるかどうか検定しなさい。」

問題1　帰無仮説はどれか。a，b のいずれかを解答欄に記入し，送信ボタンをクリックしなさい。

選択肢
a：性別で運転免許の保有率に差はない
b：性別で運転免許の保有率に差がある

解答欄：　　　　

問題2　観察された分割表の生起確率を求めなさい。答えは小数点以下 5 桁目で四捨五入した値を解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

問題3　有意水準 $5\%$ で両側検定を行うときの有意確率 $P$ を求めなさい。答えは小数点以下 5 桁目で四捨五入した値を解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

問題4　有意水準 $5\%$ で検定を行うとき，帰無仮説は棄却できるかできないか。a，b のいずれかを解答欄に記入し，送信ボタンをクリックしなさい。

選択肢
a：棄却できる
b：棄却できない

解答欄：　　　　

問題5　最終的な結論はどうなるか。a，b のいずれかを解答欄に記入し，送信ボタンをクリックしなさい。

選択肢
a：性別で運転免許の保有率に差があるとはいえない
b：性別で運転免許の保有率に差がある

解答欄：　　　　

応用問題：