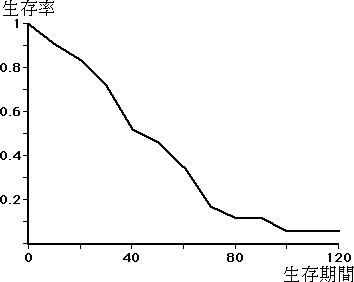
 図 1.Cutler - Ederer 法による生存率曲線 |
|---|
生命保険数理法による生命表を求める(臨床生命表とも呼ばれる。例数が少ないときには,Kaplan - Meier 法による生命表を使用すること)。
生命表の作成
Cutler - Ederer 法では,生存期間をいくつかの区間に区分して各区間での生存率を求め,それに基づいて累積生存率を求める。
表 1 のように,色の付いたセルの数値($n_1$ と $d_{i}$ ,$u_{i}+w_{i}$ ,$i = 1, 2, \dots, k$ )のみがまず埋められ,残りのセルは計算によって求める。
\[ n_i = n_{i-1} - ( d_{i-1} + u_{i-1} + w_{i-1} ), i \gt 1 \] \[ n'_{i} = n_i - \frac{u_{i} + w_{i}}{2} \]
( 1 )式でわかるように,本法では打ち切り例と脱落例を同等に扱っている。
\[ q_i = \frac{d_i}{n'_i} = \frac{d_i}{n_i-\left ( \displaystyle \frac{u_i}{2}+\frac{w_i}{2} \right )} \tag{1} \] \[ p_i = 1-q_i \tag{2} \]
\[ P_i = p_1\ p_2 \cdots p_i \tag{3} \]
表 1 および図 1 に例を示す。
| 区間 | $i$ | $n_i$ | $d_{i}$ | $u_{i}+w_{i}$ | $n'_i$ | $q_{i}$ | $p_{i}$ | $P_{i}$ | $SE(P_{i})$ |
|---|---|---|---|---|---|---|---|---|---|
| 0〜 | 1 | 37 | 3 | 8 | 33.0 | 0.09091 | 0.90909 | 0.90909 | 0.05004 |
| 10〜 | 2 | 26 | 2 | 3 | 24.5 | 0.08163 | 0.91837 | 0.83488 | 0.06813 |
| 20〜 | 3 | 21 | 3 | 1 | 20.5 | 0.14634 | 0.85366 | 0.71270 | 0.08735 |
| 30〜 | 4 | 17 | 4 | 4 | 15.0 | 0.26667 | 0.73333 | 0.52265 | 0.10356 |
| 40〜 | 5 | 9 | 1 | 0 | 9.0 | 0.11111 | 0.88889 | 0.46458 | 0.10711 |
| 50〜 | 6 | 8 | 2 | 0 | 8.0 | 0.25000 | 0.75000 | 0.34843 | 0.10729 |
| 60〜 | 7 | 6 | 3 | 0 | 6.0 | 0.50000 | 0.50000 | 0.17422 | 0.08909 |
| 70〜 | 8 | 3 | 1 | 0 | 3.0 | 0.33333 | 0.66667 | 0.11614 | 0.07600 |
| 80〜 | 9 | 2 | 0 | 0 | 2.0 | 0.00000 | 1.00000 | 0.11614 | 0.07600 |
| 90〜 | 10 | 2 | 1 | 0 | 2.0 | 0.50000 | 0.50000 | 0.05807 | 0.05595 |
| 100〜 | 11 | 1 | 0 | 0 | 1.0 | 0.00000 | 1.00000 | 0.05807 | 0.05595 |
| 110〜 | 12 | 1 | 0 | 0 | 1.0 | 0.00000 | 1.00000 | 0.05807 | 0.05595 |
| 120〜 | 13 | 1 | 0 | 1 | 0.5 | 0.00000 | 1.00000 | 0.05807 | 0.05595 |
 図 1.Cutler - Ederer 法による生存率曲線 |
|---|
生存率の比較
Cutler - Ederer 法では,各区間ごとの生存率に 2 群間で差があるかどうかを検定することができる。
\[ SE(P_i) = P_i \sqrt{\sum_{j=1}^i\frac{q_j}{n_j-\displaystyle \frac{u_j}{2}-\frac{w_j}{2}-d_j}} \tag{4} \]
\[ Z_0 = \frac{\left |\ P_a-P_b\ \right |}{\sqrt{SE_a^2+SE_b^2}} \tag{5} \]
参考文献
演習問題:
応用問題: