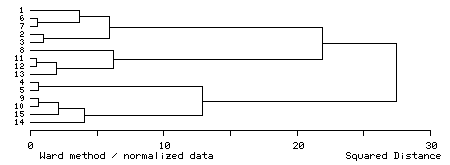
 図 1.クラスター分析の結果として得られるデンドログラム |
|---|
似通った個体あるいは変数のグループ化を行うための分析手法である。
クラスター分析の結果は,図 1 のようなデンドログラム(樹状図)として表現される。
 図 1.クラスター分析の結果として得られるデンドログラム |
|---|
個体が似通っているかどうかの判定基準としてはいくつかあるが,取り扱いが容易なユークリッド距離を用いる。
個体のクラスター分析を行う場合には,解析に用いるデータを正規化する場合としない場合では結果がかなり異なることがある。 解析に使用する変数が異なった単位で表されているときには,正規化した方がよいかもしれない。しかし,ある変数が決定的な性質を持つ場合には,正規化することは他の変数と同格に取り扱ってしまうことになるので正規化しない方がよいかもしれない。
$n$ 個の個体について,$p$ 個の変数 $X_{i1}, X_{i2}, \dots X_{ip}\ (i = 1, 2, \dots, n)$ があるとする。 初期状態として,$n$ 個のクラスターがあるとする(各クラスターは 1 個体ずつを含むと考える)。
\[ d^2_{ij} = \sum_{k=1}^p \left ( X_{ik}-X_{jk} \right ), \ (i, j = 1, 2, \dots, n) \]
\[ \begin{align*} d_{xc} &= \alpha_a\ d_{xa} + \alpha_b\ d_{xb} + \beta\ d_{ab} + \gamma\ \left |\ d_{xa} - d_{xb}\ \right | \tag{1} \\[5pt] d_{xc}^2 &= \alpha_a\ d_{xa}^2 + \alpha_b\ d_{xb}^2 + \beta\ d_{ab}^2 + \gamma\ \left |\ d_{xa}^2 - d_{xb}^2\ \right | \tag{2} \end{align*} \]
| $\alpha_a$ | $\alpha_b$ | $\beta$ | $\gamma$ | 使用される式 | |
|---|---|---|---|---|---|
| 最短距離法 | $0.5$ | $0.5$ | $0$ | $-0.5$ | ( 1 ) |
| 最長距離法 | $0.5$ | $0.5$ | $0$ | $0.5$ | ( 1 ) |
| メディアン法 | $0.5$ | $0.5$ | $-0.25$ | $0$ | ( 1 ) |
| 重心法 | $\displaystyle \frac{n_a}{n_c}$ | $\displaystyle \frac{n_b}{n_c}$ | $\displaystyle \frac{-n_a\ n_b}{n_c^2}$ | $0$ | ( 2 ) |
| 群平均法 | $\displaystyle \frac{n_a}{n_c}$ | $\displaystyle \frac{n_b}{n_c}$ | $0$ | $0$ | ( 2 ) |
| 可変法 | $\displaystyle \frac{1-\beta^*}{2}$ | $\displaystyle \frac{1-\beta^*}{2}$ | $\beta^*$ | $0$ | ( 2 ) |
| ウォード法 | $\displaystyle \frac{n_x+n_a}{n_x+n_c}$ | $\displaystyle \frac{n_x+n_b}{n_x+n_c}$ | $\displaystyle \frac{-n_x}{n_x+n_c}$ | $0$ | ( 2 ) |
( 1 )式または( 2 )式で併合後のユークリッド距離を計算するときの定数 $\alpha_a$,$\alpha_b$,$\beta$,$\gamma$ をどのように選ぶかによって,表 1 に示す 7 種類のクラスター分析が行える。
各手法の分類感度は,クラスターの融合によって空間が拡散される場合に高く,濃縮される場合に低くなる。各手法の特徴は以下の通りである。
| 手法 | 特徴 |
|---|---|
| ウォード法 | 最も明確なクラスターを作る(分類感度が高い)。 |
| 最短距離法 | 分類感度は低く,鎖状のクラスターを作る傾向がある。 |
| 最長距離法 | 空間の拡散が起こり,分類感度は高い。 |
| メディアン法 | 最近隣法と最遠隣法の折衷法である。クラスター間の距離の逆転が生じる場合がある。 |
| 重心法 | クラスター間の距離の逆転が生じる場合がある。 |
| 可変法 | パラメータ($\beta$)の選択によって空間の濃縮・拡散を制御できるので,バラエティーに富んだ結果を生み出す。$\beta$ としては1未満の値を指定する。$\beta$ の値が1に近いほど空間の濃縮が起こる(分類感度が低くなる)。負の値をとれば,空間の拡散が起こる(分類感度が高くなる)。一般に,$-0.25$〜$0$の範囲の値を与えるのがよいといわれている。 |
変数のクラスター分析を行う場合には,変数 $i$ と変数 $j$ の相関係数を $r_{ij}$ としたとき,2 変数間の距離が次式で表されることになるので,個体のクラスター分析と同じように取り扱うことができる。
\[ d^2_{ij} = 2\ (1-r_{ij}), (i,j=1, 2, \dots, p) \]
演習問題:
応用問題: