Kaplan - Meier 法による生命表 Last modified: Nov 07, 2002
Kaplan - Meier 法は,死亡発生ごとに生存率を計算するので(少数例の場合にも)正確な生存率を求めることができる(この方法は,積極限法とも呼ばれる)。
注: 少数例であっても生存率が正確に計算できるということであって,ケース数が多いときに用いてはならないということではない。
例数が多いときには,Cutler - Ederer 法が使用できる。
生命表の作成
基本的な考え方は,死亡が発生するたびに生存率を求めることから始める。
- 全観察対象数を $n$ として,死亡または打ち切り時間の小さい順に並べる。
ただし,死亡時間と打ち切り時間が同値の場合には打ち切り例が後になるように注意する。
この結果, $t_{1} \leqq t_{2} \leqq \dots \leqq t_{n}$ となったとする。
- $i$ 番目のケースが死亡した( 打切られた )時間 $t_{i}$ での生存率 $p_{i}$ は次式で定義される。
\[
p_i = \left \{
\begin{align*}
&\frac{n-i}{n-i+1}\ , &第 i ケースが死亡例のとき \\
&1\ , &第 i ケースが打切り例のとき
\end{align*}
\right .
\]
- 時点 $t_{i}$ までの累積生存率 $P_{i}$ は次式で定義される。
\[
P_i = p_1\ p_2 \dots p_i
\]
- 累積生存率の標準誤差 $SE ( P_{i} )$ は,次式となる( 死亡のあった時点でのみ求められる )。
\[
SE(P_i) = P_i \sqrt{\sum_{j=1}^i \frac{1}{(n-j+1)\ (n-j)}}
\]
表 1 および図 1 に例を示す。
 R で計算してみる
R で計算してみる
表 1.Kaplan - Meier 法による生命表
| $i$ | $t_{i}$ |
| $p_{i}$ | $P_{i}$ | $SE(P_{i})$ |
| 1 | 0 | + | 1.00000 | 1.00000 |
| 2 | 1 | + | 1.00000 | 1.00000 |
| 3 | 4 |
| 0.97143 | 0.97143 | 0.02816 |
| 4 | 4 | + | 1.00000 | 0.97143 |
| 5 | 5 | + | 1.00000 | 0.97143 |
| 6 | 6 |
| 0.96875 | 0.94107 | 0.04046 |
| 7 | 6 | + | 1.00000 | 0.94107 |
| 8 | 8 |
| 0.96667 | 0.90970 | 0.04981 |
| 9 | 9 | + | 1.00000 | 0.90970 |
| 10 | 9 | + | 1.00000 | 0.90970 |
| 11 | 9 | + | 1.00000 | 0.90970 |
| 12 | 11 | + | 1.00000 | 0.90970 |
| 13 | 15 |
| 0.96000 | 0.87331 | 0.05964 |
| 14 | 16 | + | 1.00000 | 0.87331 |
| 15 | 19 |
| 0.95652 | 0.83534 | 0.06807 |
| 16 | 19 | + | 1.00000 | 0.83534 |
| 17 | 21 |
| 0.95238 | 0.79557 | 0.07557 |
| 18 | 23 | + | 1.00000 | 0.79557 |
| 19 | 24 |
| 0.94737 | 0.75369 | 0.08238 |
| 20 | 29 |
| 0.94444 | 0.71182 | 0.08780 |
| 21 | 30 |
| 0.94118 | 0.66995 | 0.09208 |
| 22 | 32 |
| 0.93750 | 0.62808 | 0.09537 |
| 23 | 32 | + | 1.00000 | 0.62808 |
| 24 | 33 | + | 1.00000 | 0.62808 |
| 25 | 35 | + | 1.00000 | 0.62808 |
| 26 | 36 |
| 0.91667 | 0.57574 | 0.10077 |
| 27 | 37 | + | 1.00000 | 0.57574 |
| 28 | 38 |
| 0.90000 | 0.51816 | 0.10587 |
| 29 | 44 |
| 0.88889 | 0.46059 | 0.10864 |
| 30 | 55 |
| 0.87500 | 0.40302 | 0.10925 |
| 31 | 56 |
| 0.85714 | 0.34544 | 0.10775 |
| 32 | 61 |
| 0.83333 | (0.28787) | |
| 33 | 61 |
| 0.80000 | 0.23030 | 0.09788 |
| 34 | 64 |
| 0.75000 | 0.17272 | 0.08874 |
| 35 | 74 |
| 0.66667 | 0.11515 | 0.07556 |
| 36 | 95 |
| 0.50000 | 0.05757 | 0.05554 |
| 37 | 125 | + | 1.00000 | 0.05757 |
| +は打切り例 |
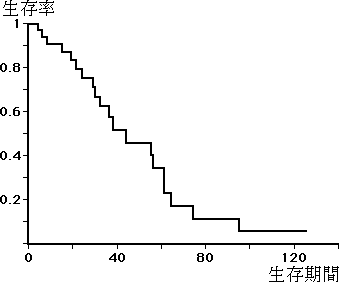 図 1.Kaplan - Meier 法による生存率曲線 |
生存期間の比較
2 群の生存時間に差があるかどうかの検定として,3 通りのノンパラメトリックな手法を紹介する。
- Cox - Mantel 検定 は,比較される両群の生存率が指数分布に従い,瞬間死亡率の比が時間の経過にかかわらず一定である場合に最も鋭敏である。
- 一般化 Wilcoxon 検定 は,比較される両群の生存率がワイブル分布などに従い,瞬間死亡率の比が時間の経過とともに変化するような場合に最も鋭敏である( 富永 1980 )。
生存率が指数分布またはワイブル分布のいずれに従うかは,生存率のグラフをみることにより判断できる。横軸に時間,縦軸に $\log( 生存率 )$ をとったグラフで生存率が直線に近ければ指数分布に従うことを意味する。横軸に $\log( 時間 )$,縦軸に $\log\{ - \log( 生存率 )\}$ をとったグラフで生存率が直線に近ければワイブル分布に従うことを意味する。
- Log rank 検定 は,生存期間をいくつかに区分して各区間ごとの $2 \times 2$ 表の $\chi^2$ 検定結果を統合するMantel - Haenszel 法に類似しているが,本法は生存期間の区分をしないので Mantel - Haenszel 法より優れている。
参考文献
- 青木繁伸, 開原成允: 生命表による生存曲線の解析 - - 医学統計学最近の話題( 2 ). 医学のあゆみ, 104 ( 9 ) , 587 - 592, 1978.
- 富永祐民: 治療効果判定のための実用統計学 − 生命表法の解説 − . 蟹書房, 東京, 1980.
- Cox, D. R.: Regression models and life tables. J. R. Stat. Soc. [B], 34 , 187 - 220, 1972.
- Gehan, E. A.: A generalized Wilcoxon test for comparing arbitrarily singly-censored samples. Biometrika, 52 , 203 - 223, 1965.
- Kaplan, E. L. and Meier, P.: Nonparametric estimation from incomplete observations. J. Am. Statist. Assoc., 53 , 457 - 481, 1958.
- Mantel, N.: Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemother. Rep., 50 , 163 - 170, 1966.
- Mantel, N.: Ranking procedures for arbitrarily restricted observations. Biometrics, 23 , 65 - 78, 1967.
- Peto, R., Pike, M. C., Armitage, N. E. et al: Design and analysis of randomized clinical trials requiring prolonged observation of each patient. II. Analysis and examples. Br. J. Cancer, 35 , 1 - 39, 1977.
演習問題:
応用問題:
 計算プログラム [R] [Python]
計算プログラム [R] [Python]
 直前のページへ戻る
直前のページへ戻る  E-mail to Shigenobu AOKI
E-mail to Shigenobu AOKI
