適合度の検定−−正規分布への適合度の検定
Last modified: Jun 01, 2006
例題:
「体重を測定した結果(測定精度は 0.1kg)が表 1 のようにまとめられた(表の左2列)。このデータは正規分布に従っているといえるだろうか。」
表 1.体重の分布
| 階級 | 度数 $f$ | 下限点 | 上限点 | 級中心 $x$ | $f\cdot x$ | $f\cdot x^{2}$ | $z$ | $F(z)$ | 理論比 | 期待値 |
| 35〜 | 0 | 34.95 | 39.95 | 37.45 | 0.00 | 0.00 | -3.50 | 0.0002 | 0.0002 | 0.098 |
| 40〜 | 4 | 39.95 | 44.95 | 42.45 | 169.80 | 7208.01 | -2.53 | 0.0057 | 0.0055 | 2.340 |
| 45〜 | 19 | 44.95 | 49.95 | 47.45 | 901.55 | 42788.55 | -1.55 | 0.0600 | 0.0543 | 23.124 |
| 50〜 | 86 | 49.95 | 54.95 | 52.45 | 4510.70 | 236586.22 | -0.58 | 0.2807 | 0.2207 | 94.020 |
| 55〜 | 177 | 54.95 | 59.95 | 57.45 | 10168.65 | 534188.94 | 0.39 | 0.6529 | 0.3722 | 158.568 |
| 60〜 | 105 | 59.95 | 64.95 | 62.45 | 6557.25 | 409500.26 | 1.37 | 0.9142 | 0.2613 | 111.310 |
| 65〜 | 33 | 64.95 | 69.95 | 67.45 | 2225.85 | 150133.58 | 2.34 | 0.9904 | 0.0762 | 32.446 |
| 70〜 | 2 | 69.95 | 74.95 | 72.45 | 144.90 | 10498.01 | 3.32 | 0.9995 | 0.0092 | 3.899 |
| 75〜 | 0 | 74.95 | 79.95 | 77.45 | 0.00 | 0.00 | 4.29 | 1.0000 | 0.0005 | 0.195 |
| 合計 | 426 |
|
|
| 24678.70 | 1440893.57 |
|
| 1.0000 | 426.000 |
注:母平均,母分散が既知の場合には以下の方法ではなく,名義尺度の場合 または 順序尺度以上の場合(1 標本コルモゴロフスミルノフ検定)により検定を行う。
検定手順:
- 前提
- 帰無仮説 $H_0$:「母分布は正規分布である」。
- 対立仮説 $H_1$:「母分布は正規分布ではない」。
- 有意水準 $\alpha$ で両側検定を行う(片側検定は定義できない)。
- まず最初に,正規分布のパラメータを推定する。
注:測定値の分布に正規分布をあてはめるときには一般に母平均,母分散がわからないので,以下のように標本値で代用しなければならない。
- $n$ 個のケースが,$k$ 個のカテゴリーに分類されているとする。
\[
n = \sum_{i=1}^k f_i
\]
例題では,$n = 426$,$k = 9$(階級「35〜」と「75〜」は以下の計算を行うために作られたものである)。
- 各階級の中心点を $X_{i}$,観測度数を $f_{i}$ とする。
例題では,測定精度が 0.1 kg なので,たとえば「50kg 以上 55kg 未満」という階級の真の限点は 49.95kg と 54.95kg である。級中心はその中点で,52.45kg である(50kg と 55kg の中点の 52.5kg ではないことに注意)。
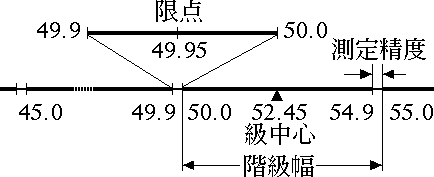 図 1.限点・級中心の定義 |
- 与えられた度数分布表から,母平均と母分散の推定値 $\bar{X}$,$V$ を推定する。
\[
\begin{align*}
\bar{X} & = \frac{\displaystyle \sum_{i=1}^k f_i\,X_i}{n} \\
V & = \frac{\displaystyle n\sum_{i=1}^k f_i\,X_i^2 - \left(\sum_{i=1}^k f_i\,X_i\right)^2}{n^2}
\end{align*}
\]
例題では,表 1 の 6 列目の合計欄の $24678.70$ を $n = 426$ で割って,$\bar{X} = 57.9312$,7 列目の合計欄の $1440893.57$ を用いて $V = 26.3528$。
- 第 $i$ 階級と第 $i+1$ 階級の限点を $X'_{i}$,それに対する標準化得点を $Z_{i}$ とする。
\[
Z_i = \frac{X_i'-\bar{X}}{\sqrt{V}}
\]
例題では,表 1 の 8 列目。
- 各 $Z_{i}$ から $Z \lt Z_{i}$ となる確率 $P_{i}$ を求め(標準正規分布表,または正規分布の上側確率の計算を参照する),差をとることにより各階級の確率 $p_{i} = P_{i} - P_{i-1}\ (i = 2, 3, \dots , k-1)$ を求める。
$p_{1} = \Pr\{Z \lt Z_{1}\}$
$p_{k} = 1 - ( p_{1} + p_{2} + \dots + p_{k-1} )$。
例題では,表 1 の 9,10 列目。
- 理論度数は,$E_{i} = n p_{i}$ となる。
例題では,表 1 の 11 列目。
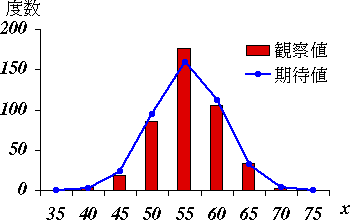 図 2.あてはめ結果 |
- 期待値が $1$ 以下のカテゴリーを併合する。併合後のカテゴリー数を m とする。
例題では,表 1 の最初の 2 行を一つに合併し,最後の 2 行を一つに合併する。$m = 7$ である。
- 以下の式で検定統計量を計算する。
\[
\chi^2_0 = \sum_{i=1}^m \frac{\left(\ f_i - E_i\ \right)^2}{E_i}
\]
例題では,
$\chi^2_0 = 6.000$ となる。
- $\chi^2_0$ は,自由度が $m - 1 - 2$ の $\chi^2$ 分布に従う(母平均と母分散の推定を行ったため,自由度が $2$ だけ余分に減る。)
例題では,自由度が $7 - 1 - 2 = 4$ の $\chi^2$ 分布に従うことになる。
- 有意確率を $P = \Pr\{\chi^2 \geqq \chi^2_0\}$ とする。
$\chi^2$ 分布表,または $\chi^2$ 分布の上側確率の計算を参照すること。
例題では,自由度 $4$ の $\chi^2$ 分布において,$\Pr\{\chi^2 \geqq 9.49\}= 0.05$ であるから,$P = \Pr\{\chi^2 \geqq 6.000\}\gt 0.05$ である(正確な有意確率:$P = 0.199$)。
- 帰無仮説の採否を決める。
- $P \gt \alpha$ のとき,帰無仮説は棄却できない。「母分布は正規分布でないとはいえない」。
- $P \leqq \alpha$ のとき,帰無仮説を棄却する。「母分布は正規分布ではない」。
例題では,有意水準 $5\%$ で検定を行うとすれば($\alpha = 0.05$),$P \gt \alpha$ であるから,帰無仮説は棄却できない。すなわち,「正規分布に従っていないとはいえない」。
 R で計算してみる
R で計算してみる
 計算プログラム [R] [Python]
計算プログラム [R] [Python]
演習問題:
応用問題:
「知能指数 IQ の平均値は 100,標準偏差は 16 の正規分布に従うといわれる。ある集団で調査したところ表 2 のような結果であった。この集団の IQ は正規分布に従っているといえるだろうか。」
表 2.知能指数 IQ は正規分布 $\mathcal{N}(100, 16^{2})$ に従うかどうか
| 知能指数 | 76 未満 | 76 〜 92未満 | 92 〜 108未満 | 108 〜124未満 | 124 以上 | 合計 |
| 観察度数 | 9 | 49 | 101 | 76 | 18 | 253 |
問題1 このページで説明した検定手法を使うべきか。a,b,c のいずれかを解答欄に記入し,送信ボタンをクリックしなさい。
解説(コメント)
問題2 知能指数が 76 であるとき,標準化得点を解答欄に記入し,送信ボタンをクリックしなさい。
問題3 知能指数が 76 未満の理論比を正規分布表から読みとり,小数点以下 5 桁目で四捨五入した値を解答欄に記入し,送信ボタンをクリックしなさい。
問題4 $\chi^2_0$ を計算し,小数点以下 3 桁目で四捨五入した値を解答欄に記入し,送信ボタンをクリックしなさい。
問題5 計算された $\chi^2_0$ は自由度がいくつの $\chi^2$ 分布に従うか。解答欄に記入し,送信ボタンをクリックしなさい。
問題6 有意確率は $0.05$ より大きいか小さいか。a,b のいずれかを解答欄に記入し,送信ボタンをクリックしなさい。
問題7 有意水準 $5\%$ で検定を行うとき,帰無仮説は棄却できるかできないか。a,b のいずれかを解答欄に記入し,送信ボタンをクリックしなさい。
問題8 最終的な結論はどうなるか。a,b のいずれかを解答欄に記入し,送信ボタンをクリックしなさい。
 計算プログラム [R] [Python]
計算プログラム [R] [Python]
 直前のページへ戻る
直前のページへ戻る  E-mail to Shigenobu AOKI
E-mail to Shigenobu AOKI

