目的

正規分布への適合度の検定を行う

使用法

normaldist(x, b, w, a)
sumamry.normaldist(obj, digits=5)
plot.normaldist(obj, xlab="", ylab="Frequency", ...)

引数

x	度数ベクトル
b	度数分布表の最初の階級の下限値
w	階級幅
a	測定精度
org     normaldist 関数が返すオブジェクト
digits  表示桁数
xlab, ylab 軸の名前
...     plot に渡す引数

ソース

インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/normaldist.R", encoding="euc-jp")

# 正規分布への適合度の検定
normaldist <- function(      x,                                              # 度数ベクトル
                        b,                                              # 最初の階級の下限値
                        w,                                              # 階級幅
                        a)                                              # 測定精度
{
        data.name <- deparse(substitute(x))
        method <- "正規分布への適合度の検定" 
        n <- sum(x)                                                  # データ数
        x <- c(0, x, 0)                                                      # 上下にそれぞれ 1 階級を追加する
        k <- length(x)                                                       # 階級数
        mid <- seq(b-w/2, b+k*w-w, w)-a/2                            # 級中心

        xbar <- sum(mid*x)/n                                         # 平均値
        variance <- sum(x*(mid-xbar)^2)/n                            # 分散（不偏分散ではない）
        SD <- sqrt(variance)                                         # 標準偏差
        result <- c("n"=n, "Mean"=xbar, "Variance"=variance, "S.D."=SD)

        z <- ((mid+w/2)-xbar)/SD                                     # 級限界の標準化得点
        p <- pnorm(z)                                                        # 累積確率
        p[k] <- 1                                                    # 最後の累積確率は 1
        p <- p-c(0, p[-k])                                           # 各階級の確率
        expectation <- n*p                                           # 各階級の期待値
        table <- data.frame(mid, x, z, p, expectation)                       # 結果をデータフレームにする
        rownames(table) <- paste("c-", 1:k, sep="")

        while (expectation[1] < 1) {                                 # 期待値が 1 未満の階級を併合
                x[2] <- x[2]+x[1]
                expectation[2] <- expectation[2]+expectation[1]
                x <- x[-1]
                expectation <- expectation[-1]
                k <- k-1
        }
        while (expectation[k] < 1) {                                 # 期待値が 1 未満の階級を併合
                x[k-1] <- x[k-1]+x[k]
                expectation[k-1] <- expectation[k-1]+expectation[k]
                x <- x[-k]
                expectation <- expectation[-k]
                k <- k-1
        }
        chisq <- sum((x-expectation)^2/expectation)                  # カイ二乗統計量
        df <- k-3                                                    # 自由度
        p <- pchisq(chisq, df, lower.tail=FALSE)                     # P 値
        names(chisq) <- "X-squared"
        names(df) <- "df"
        return(structure(list(statistic=chisq, parameter=df, p.value=p,
                estimate=c(n=n, Mean=xbar, Variance=variance, S.D.=SD),
                method=method, data.name=data.name, table=table),
                class=c("htest", "normaldist")))
}
# summary メソッド
summary.normaldist <- function(      obj,                                    # normaldist が返すオブジェクト
                                digits=5)                               # 表示桁数
{
        table <- obj$table
        colnames(table) <- c("級中心", "度数", "標準化得点", "確率", "期待値")
        cat("\n適合度\n\n")
        print(table, digits=digits, row.names=FALSE)
}
# plot メソッド
plot.normaldist <- function( obj,                                    # normaldist が返すオブジェクト
                                xlab="", ylab="Frequency",              # 軸の名称
                                ...)                                    # plot に渡す引数
{
        d <- obj$table
        class <- d$mid
        w <- diff(class)[1]
        class <- class-w/2
        k <- length(class)
        yo <- d$x
        ye <- d$expectation
        plot(c(class[1], class[k]+w), c(0, max(c(yo, ye))), type="n", xlab=xlab, ylab=ylab, ...)
        rect(class, 0, class+w, yo, col="grey")
        Mean <- obj$estimate[2]
        SD <- obj$estimate[4]
        x <- seq(class[1], class[k]+w, length=2000)
        y <- dnorm(x, mean=Mean, sd=SD)*sum(yo)*w
        lines(x, y)
        x <- d$mid
        y <- dnorm(x, mean=Mean, sd=SD)*sum(yo)*w
        points(x, y, pch=3)
}


使用例

> x <- c(4, 19, 86, 177, 105, 33, 2)
> (a <- normaldist(x, 40, 5, 0.1))	# 検定結果

	正規分布への適合度の検定

data:  x 
X-squared = 6.0002, df = 4, p-value = 0.1991
sample estimates:
         n       Mean   Variance       S.D. 
426.000000  57.931221  26.352934   5.133511 

> summary(a)	# 適合度


適合度

 級中心 度数 標準化得点       確率     期待値
  37.45    0   -3.50271 0.00023027   0.098096
  42.45    4   -2.52872 0.00549367   2.340301
  47.45   19   -1.55473 0.05428132  23.123842
  52.45   86   -0.58074 0.22070354  94.019709
  57.45  177    0.39326 0.37222567 158.568133
  62.45  105    1.36725 0.26129165 111.310243
  67.45   33    2.34124 0.07616398  32.445853
  72.45    2    3.31523 0.00915208   3.898785
  77.45    0    4.28922 0.00045784   0.195038

> plot(a)	# 図に表示



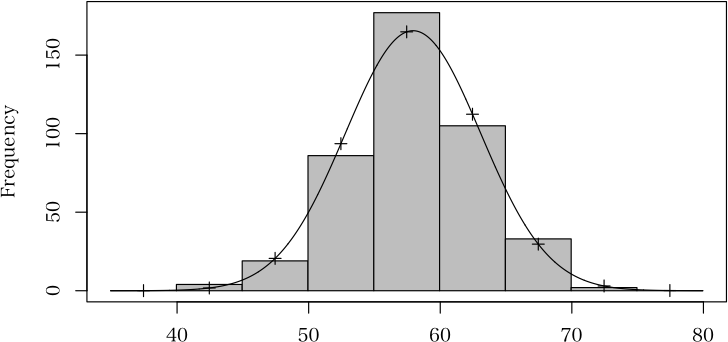
 解説ページ