例題：

　「サイコロを 56 回振って目の出方を調べたところ，表 1 のようになった。このサイコロは正しいサイコロといえるだろうか。」

検定手順：

1. 前提
   • 帰無仮説 $H_0$：「各カテゴリーの理論比が $p_{i}\ (i=1, 2, \dots , k)$ である」。
   • 対立仮説 $H_1$：「各カテゴリーの理論比が $p_{i}\ (i=1, 2, \dots , k)$ ではない」。
   • 有意水準 $\alpha$ で両側検定を行う（片側検定は定義できない）。

2. $n$ 個のケースが，$k$ 個のカテゴリーに分類されているとする。

   例題では，$n = 56$，$k = 6$ である。

3. $O_{i}$：　第 $i$ カテゴリーの観察値

   例題では，$O_{1} = 10, O_{2} = 12, \dots , O_{6} = 8$ である。

4. $E_{i} = n p_{i}$ ：　第 $i$ カテゴリーの期待値

   例題では，正しいサイコロならば，どの目の出る確率も等しく $\displaystyle \frac{1}{6}$ であるはずである（$p_{1} = p_{2} = \dots = p_{6} = 1/6$ ）。
   したがって，各目の出る期待値は，$E_{1} = E_{2} = \dots = E_{6} =56\times \displaystyle \frac{1}{6} = 9.333$ である。

5. 期待値が $1$ 以下のカテゴリーを併合する。併合後のカテゴリー数を $m$ とする。

   例題では，このステップは不要である。
   $m = k = 6$ である。

6. 以下の式で検定統計量を計算する。 \[ \chi^2_0 = \sum_{i=1}^m \frac{\left(\ O_i-E_i\ \right)^2}{E_i} \] 例題では，$\chi^2_0 = \displaystyle \frac{\left (10-\displaystyle \frac{56}{6} \right )^{2}+ \left (12-\displaystyle \frac{56}{6} \right )^{2}+ \dots + \left ( 8-\displaystyle \frac{56}{6} \right )^{2} } {\displaystyle \frac{56}{6}} = 5.5$ となる。

7. $\chi^2_0$ は，自由度が $m-1$ の $\chi^2$ 分布に従う。

   例題では，自由度が $5$ の $\chi^2$ 分布に従う。

8. 有意確率を $P = \Pr\{\chi^2 \geqq \chi^2_0\}$ とする。
   $\chi^2$ 分布表，または $\chi^2$ 分布の上側確率の計算を参照すること。

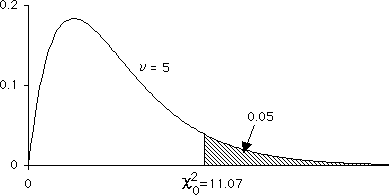
   例題では，自由度 $5$ の $\chi^2$ 分布において，$\Pr\{\chi^2 \geqq 11.07\}= 0.05$ であるから，$P = \Pr\{\chi^2 \geqq 5.5\}\gt 0.05$ である（正確な有意確率：$P = 0.3579459$）。

   

9. 帰無仮説の採否を決める。
   • $P \gt \alpha$ のとき，帰無仮説は棄却できない。「所与の理論比に従っていないとはいえない」。
   • $P \leqq \alpha$ のとき，帰無仮説を棄却する。「所与の理論比に従っていない」。

   例題では，有意水準 $5\%$ で検定を行うとすれば（$\alpha = 0.05$），$P \gt \alpha$ であるから，帰無仮説は棄却できない。すなわち，「サイコロの目の出方は等しくないとはいえない」。

注１：理論比が一定 $p_{i}\ (i=1, 2, \dots , k)$ の場合は，特に一様性の検定と呼ばれる。

注２：順序尺度データ以上の場合には，もっと適切な検定手法がある。

演習問題：

　「表 2 において，表現形質が 9：3：3：1 になっているかどうか検定しなさい。」

問題1　帰無仮説はどれか。a，b のいずれかを解答欄に記入し，送信ボタンをクリックしなさい。

選択肢
a：表現形質がメンデルの遺伝法則に従う
b：表現形質がメンデルの遺伝法則に従わない

解答欄：　　　　

問題2　表現形質が aB であるものの期待値を求めなさい。答えは小数点以下 4 桁まで正確に求め，解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

問題3　$\chi^2_0$ 検定統計量を求めなさい。答えは小数点以下 4 桁目で四捨五入した値を解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

問題4　求められた $\chi^2_0$ 検定統計量は，自由度いくつの $\chi^2$ 分布に従うか，答えを解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

問題5　有意確率は 0.05 より大きいか小さいか。a，b のいずれかを解答欄に記入し，送信ボタンをクリックしなさい。

選択肢
a：0.05 より大きい
b：0.05 より小さい

解答欄：　　　　

問題6　有意水準 $5\%$ で検定を行うとき，帰無仮説は棄却できるかできないか。a，b のいずれかを解答欄に記入し，送信ボタンをクリックしなさい。

選択肢
a：棄却できる
b：棄却できない

解答欄：　　　　

問題7　最終的な結論はどうなるか。a，b のいずれかを解答欄に記入し，送信ボタンをクリックしなさい。

選択肢
a：表現形質はメンデルの遺伝法則に従わないとはいえない
b：表現形質はメンデルの遺伝法則に従わない

解答欄：　　　　

応用問題：