漸近指数曲線　　$Y=ab^X+c$　　　　　Last modified: Sep 08, 2009

例題：

　「表 1 に示すようなデータに曲線をあてはめなさい。」

表 1．テストデータ
$X$ 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
$Y$ 52 53 56 60 68 81 104 144 212 331 536

考え方：

  1. 元のデータをプロットすると図 1 のようになる。

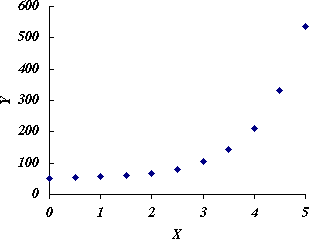
    figure

    図 1．元データのプロット

  2. 　母回帰関数を，$f ( \alpha, \beta, \gamma ) = \alpha\ \beta^{X} + \gamma$ とする。

    この関数は母数 $\beta$ について非線形であるため，線形近似を行い，繰返し計算でパラメータを推定する。

    1. $u_{1}$ を $\beta$ の第 $1$ 近似とすると，テーラー展開によって，$\alpha\ \beta^X+\gamma ≒ \alpha\ u_1^X + \alpha\ (\beta-u_1)\ X\ u_1^{X-1}+\gamma $ となる。

    2. $V = u_{1}^{X}$，$W = X u_{1}^{X - 1}$ とおいて，$Y = a\ V + b\ W + c$ なる重回帰式を求める。

    3. 求めるパラメータの第 $2$ 近似は，$\gamma = c$，$\alpha = a$，また，$b = a（ u_{2} - u_{1} ）$より，

      $\beta$ の第 $2$ 近似は $u_{2} = u_{1} + b / a$ となる。

    4. この繰返し計算を $b / a$ が十分小さくなるまで繰返す。

      例題では初期値として u1 = 2.59748427672956 から出発することにより以下のような繰り返しで解が求まる。

      
u1 = 2.59748427672956                  
        X         Y         V         W  
       0.0      52.0     1.000     0.000 
       0.5      53.0     1.612     0.310 
       1.0      56.0     2.597     1.000 
       1.5      60.0     4.186     2.418 
       2.0      68.0     6.747     5.195 
       2.5      81.0    10.874    10.466 
       3.0     104.0    17.525    20.241 
       3.5     144.0    28.245    38.058 
       4.0     212.0    45.521    70.100 
       4.5     331.0    73.365   127.101 
       5.0     536.0   118.240   227.605 
Y = 1.3572378951535393 V + 1.4243549394066728 W + 50.96792725159578 
u2 = 2.59748427672956 + 1.4243549394066728 / 1.3572378951535393 = 3.646935477946971 
        X         Y         V         W  
       0.0      52.0     1.000     0.000 
       0.5      53.0     1.910     0.262 
       1.0      56.0     3.647     1.000 
       1.5      60.0     6.965     2.865 
       2.0      68.0    13.300     7.294 
       2.5      81.0    25.399    17.411 
       3.0     104.0    48.505    39.900 
       3.5     144.0    92.629    88.897 
       4.0     212.0   176.894   194.019 
       4.5     331.0   337.813   416.832 
       5.0     536.0   645.120   884.468 
Y = 1.5580545437279183 V - 0.5886346410044238 W + 51.059342456915786 
u3 = 3.646935477946971 - 0.5886346410044238 / 1.5580545437279183 = 3.269134428956727 
        X         Y         V         W  
       0.0      52.0     1.000     0.000 
       0.5      53.0     1.808     0.277 
       1.0      56.0     3.269     1.000 
       1.5      60.0     5.911     2.712 
       2.0      68.0    10.687     6.538 
       2.5      81.0    19.323    14.777 
       3.0     104.0    34.938    32.062 
       3.5     144.0    63.171    67.632 
       4.0     212.0   114.217   139.752 
       4.5     331.0   206.513   284.268 
       5.0     536.0   373.391   571.085 
Y = 1.899365987004002 V - 0.3910797118708441 W + 50.049483470128614 
u4 = 3.269134428956727 - 0.3910797118708441 / 1.899365987004002 = 3.063234294624154 
        X         Y         V         W  
       0.0      52.0     1.000     0.000 
       0.5      53.0     1.750     0.286 
       1.0      56.0     3.063     1.000 
       1.5      60.0     5.361     2.625 
       2.0      68.0     9.383     6.126 
       2.5      81.0    16.423    13.403 
       3.0     104.0    28.744    28.150 
       3.5     144.0    50.307    57.480 
       4.0     212.0    88.048   114.974 
       4.5     331.0   154.103   226.383 
       5.0     536.0   269.713   440.241 
Y = 2.0172279573118015 V - 0.13132147277444592 W + 49.759579890674324 
u5 = 3.063234294624154 - 0.13132147277444592 / 2.0172279573118015 = 2.9981343279602735 
        X         Y         V         W  
       0.0      52.0     1.000     0.000 
       0.5      53.0     1.732     0.289 
       1.0      56.0     2.998     1.000 
       1.5      60.0     5.191     2.597 
       2.0      68.0     8.989     5.996 
       2.5      81.0    15.564    12.978 
       3.0     104.0    26.950    26.966 
       3.5     144.0    46.664    54.475 
       4.0     212.0    80.799   107.799 
       4.5     331.0   139.904   209.986 
       5.0     536.0   242.245   403.993 
Y = 2.0281494984405004 V + -0.012421069396475732 W + 49.7352498940903 
u6 = 2.9981343279602735 + -0.012421069396475732 / 2.0281494984405004 = 2.99200999175822 
        X         Y         V         W  
       0.0      52.0     1.000     0.000 
       0.5      53.0     1.730     0.289 
       1.0      56.0     2.992     1.000 
       1.5      60.0     5.175     2.595 
       2.0      68.0     8.952     5.984 
       2.5      81.0    15.485    12.939 
       3.0     104.0    26.785    26.856 
       3.5     144.0    46.331    54.197 
       4.0     212.0    80.141   107.139 
       4.5     331.0   138.622   208.489 
       5.0     536.0   239.781   400.703 
Y = 2.028234388008558 V + -0.00010116737107210208 W + 49.73508927657924 
u7 = 2.99200999175822 + -0.00010116737107210208 / 2.028234388008558 = 2.9919601122316375 
        X         Y         V         W  
       0.0      52.0     1.000     0.000 
       0.5      53.0     1.730     0.289 
       1.0      56.0     2.992     1.000 
       1.5      60.0     5.175     2.595 
       2.0      68.0     8.952     5.984 
       2.5      81.0    15.484    12.938 
       3.0     104.0    26.784    26.855 
       3.5     144.0    46.328    54.195 
       4.0     212.0    80.135   107.134 
       4.5     331.0   138.612   208.477 
       5.0     536.0   239.761   400.676 
Y = 2.0282343471966158 V + 0.000000021292892722326665 W + 49.735089572519655 
u8 = 2.9919601122316375 + 0.000000021292892722326665 / 2.0282343471966158 = 2.9919601227298784

あてはめの結果，$a$ は $V$ の係数 2.0282343471966158，$b$ は $u_{8}$ = 2.9919601227298784，$c$ は定数項 49.735089572519655 となる。

　予測値 $= 2.0282343471966158 \times 2.9919601227298784 ^ x + 49.735089572519655 $ 

 
         X         Y    予測値 
   0.00000  52.00000  51.76332 
   0.50000  53.00000  53.24338 
   1.00000  56.00000  55.80349 
   1.50000  60.00000  60.23177 
   2.00000  68.00000  67.89149 
   2.50000  81.00000  81.14073 
   3.00000 104.00000 104.05831 
   3.50000 144.00000 143.69951 
   4.00000 212.00000 212.26801 
   4.50000 331.00000 330.87289 
   5.00000 536.00000 536.02710

・ パラメータと関数の概形の関連

・ R で計算してみる

演習問題：

応用問題：

・ 直前のページへ戻る　　・ E-mail to Shigenobu AOKI