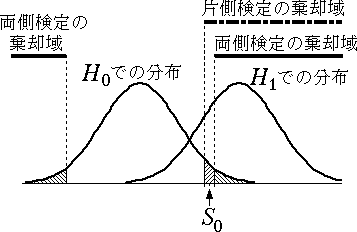
 図 8.片側検定と両側検定の棄却域 |
|---|
検出力は $( 1 - \beta )$ によって定義され ,“$H_0$ が誤っているときに,$H_0$ を棄却できる確率”である。
両側検定を用いると,$H_0$ が誤っている場合にも $H_0$ を棄却できる確率が低くなる。 図 8 にその状況を示す。$S_{0}$ という統計量が得られても,片側検定では $H_0$ を棄却できるが両側検定では棄却できない。このことから,「両側検定は片側検定より検出力は低い」ことがわかる。
 図 8.片側検定と両側検定の棄却域 |
|---|
例として,母集団が標準正規分布に従う場合を考える。すなわち,$\mu = 0$,$\sigma = 1$ である。
まず,両側検定の場合を考えてみよう。$H_0$: $\theta = \mu$,$H_1$: $\theta \ne \mu$ である。 対立仮説の一つの例として,$\theta = 1$ の場合,帰無仮説の下で,図 9 のように表すことができる。 例えば右側に棄却域を設ける片側検定において,真値が左側にあるような場合には,検出力は両側検定に比べて極端に小さくなる。片側検定は両側検定に比べて検出力が高いと言われる。 この根底には,図 5 のようなことはない,すなわち,$H_1$ 自体が完全に誤っていることはないはずだという前提があるためである。 この前提は,それまでに得られた知見で十分支持されていなければならない。 したがって,「片側検定は両側検定に比べて検出力が高いからといっても,既に述べた前提(仮説の方向性)が不確かな場合には片側検定を用いてはならない」ということになる。
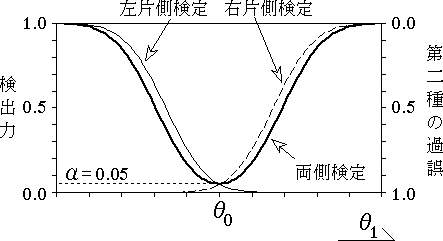 図 9.片側検定と両側検定の検出力 |
|---|
検出力に影響する諸要因
検出力は既に述べたように片側検定と両側検定で異なる。この他にも検出力に関係する要因がいくつかある。
この違いは特に,パラメトリックな手法とノンパラメトリックな手法で大きく違う。
代表値の差の検定としてパラメトリックな手法の $t$ 検定の効率を 1 とすると,ノンパラメトリックな手法でそれに対応する中央値検定の効率は $0.63$,マン・ホイットニーの $U$ 検定の効率は $0.95$ といわれる。つまり,標本の大きさが $n$ であるとき,$t$ 検定と同じ検出力を期待するならば,中央値検定では $n\ /\ 0.63 = 1.59\ n$ の標本が必要だということを意味する。
効率の違いは,データに含まれる情報をどの程度まで利用しているかによる。
標本サイズが大きくなるにつれ,母数に関する情報は多くなり,それだけ第 $1$ 種,第 $2$ 種の誤差は小さくなり,したがって,検出力は高くなる。
演習問題:
応用問題: