“帰無仮説 $H_0$ が誤っているにもかかわらず，$H_0$ を棄却できない誤り”を第 $2$ 種の過誤と呼び，$\beta$ で表される。

• 片側検定の場合 を図 4，図 5 に示す。

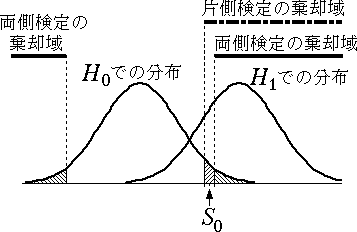
  図 4 は $\theta_{0}$ と $\theta_{1}$ の大小関係と棄却域（検定統計量がその範囲の値をとったときに帰無仮説が棄却されるような領域）のある方向が一致したとき， 図 5 は一致しなかったときである。図 5 のようなことは，新薬は旧薬より有効であるという作業仮説が全く誤っていた場合に相当するが， このようなことは通常はめったに起こり得ないし，あってはならないことである。しかし，万一のことを考えて， 両側検定を行えばこのような悲劇的な状況は避けることができる。

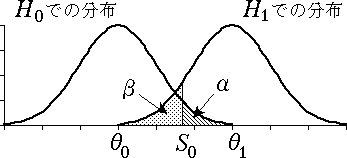  図 4．片側検定の場合の第 $2$ 種の過誤（$\theta_{0} \lt \theta_{1}$）

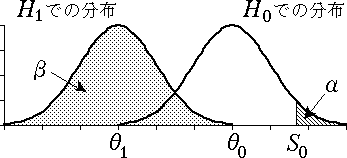  図 5．片側検定の場合の第 $2$ 種の過誤（$\theta_{0} \gt \theta_{1}$）

• 両側検定の場合 を図 6，図 7 に示す。

  $\theta_{0} \lt \theta_{1}$，$\theta_{1} \lt \theta_{0}$ のいずれの場合にも $\beta$ はあまり大きくはならない。 つまり，母数 $\theta$ の全変域を考えた両側検定においては片側検定のときのような破滅的な状況は生じない。

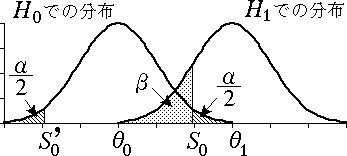  図 6．両側検定の場合の第 $2$ 種の過誤（$\theta_{0} \lt \theta_{1}$）

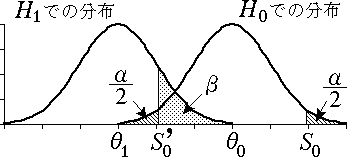  図 7．両側検定の場合の第 $2$ 種の過誤（$\theta_{0} \gt \theta_{1}$）

　しかし，そうだからといって両側検定を用いると，$H_0$ が誤っている場合にも $H_0$ を棄却できる確率が低くなるという問題が生ずる。 図 8 にその状況を示す。$S_{0}$ という統計量が得られても，片側検定では $H_0$ を棄却できるが両側検定では棄却できない。検出力の項を参照のこと。

図 8．片側検定と両側検定の棄却域

演習問題：

応用問題：