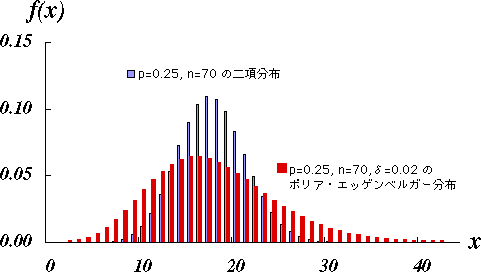
 図 1.ポリア・エッゲンベルガー分布の概形 |
|---|
壷の中に合計 $N$ 個の白玉と黒玉が入っている。白玉と黒玉の比率をそれぞれ $p$,$q$( $p + q = 1$ )とすると, 白玉は $p\ N$ 個,黒玉は $q\ N$ 個である。この中から 1 個の玉を取り出したときその玉が
$n$ 回のうち $x$ 回白玉を取り出すとすると $n - x$ 回は黒玉を取り出すことになる。$\delta = d\ /\ N$ とおくと,この確率は,$x \geqq 1$ のとき, \[ f(x) = {n \choose x}\cdot p\cdot \frac{p+\delta}{1+\delta} \cdots \frac{p+(x-1)\ \delta}{1+(x-1)\ \delta}\cdot \frac{q}{1+x\delta}\cdot \frac{q+\delta}{1+(x+1)\ \delta} \cdots \frac{q+(n-x-1)\ \delta}{1+(n-1)\ \delta} \tag{1} \] となり,$x = 0$ のときは, \[ f(0)= \prod_{k=0}^{n-1}\frac{q+k\ \delta}{1+k\ \delta} \tag{2} \] となる。
ここで,$\delta$ は伝播係数と呼ばれるもので,$\delta = 0$ すなわち玉を追加しないときには,二項分布に一致し,$\delta \gt 0 $の場合が ポリア・エッゲンベルガー分布 と呼ばれる。
 図 1.ポリア・エッゲンベルガー分布の概形 |
|---|
ここでさらに,$n\ p = \lambda$( 一定 ),$n \delta = r$ とおき,$n\rightarrow \infty$ とすると,( 1 )式は, \[ f(x) = \frac{\lambda^x}{x!} (1+r)^{-\lambda/r-x}\ \prod_{k=0}^{x-1} \left(1+\frac{k\ r}{\lambda} \right) \tag{3} \] また,( 2 )式は, \[ f(0)= (1+r)^{-\lambda/r} \tag{4} \] となる。
ここで,( 3 )式と( 4 )式をあわせると,$r \rightarrow 0$ のときポアソン分布となる。
さらに,( 3 )式と( 4 )式の分布は, \[ f(x) = {-\lambda/r \choose x} \left( \frac{1}{1+r} \right)^{\lambda/r} \left( -\frac{r}{1+r} \right) ^x \] と変形でき,負の二項分布の( 2 )式で,$k = \lambda\ /\ r$,$p = 1\ /\ ( 1 + r )$ とした場合に完全に一致する。すなわち,( 3 )式は負の二項分布を表しているのでポリア型の負の二項分布とも呼ばれる。
したがって,平均 $E ( x )$ ,分散 $V ( x )$ は
\[ E ( x ) = \lambda,\ V ( x ) = \lambda ( 1 + r ) \] である。
一日の交通事故の死亡者数はポアソン分布にあてはめるが,分散は平均値より若干大きくなる傾向がある。このような場合にはポリア・エッゲンベルガー分布によくあてはまることがある。つまり,極めてまれにしか起こらない事象でかつ以前の事象が次の事象に影響を及ぼす場合によくあてはまる。コレラなどの伝染病の発生数のモデルなどに有用である。
演習問題:
応用問題: