目的

ポリヤ・エッゲンベルガー分布への適合度の検定を行う

使用法

PolyaEggenbergerdist(d, x)
summary.PolyaEggenbergerdist(obj, digits=5)
plot.PolyaEggenbergerdist(obj, ...)

引数

d       度数ベクトル
x       階級値ベクトル
obj     PolyaEggenbergerdist 関数が返すオブジェクト
digits  表示桁数
...     barplot に渡す引数

ソース

インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/PolyaEggenbergerdist.R", encoding="euc-jp")

# ポリヤ・エッゲンベルガー分布への適合度の検定
PolyaEggenbergerdist <- function(d,             # 度数ベクトル
                                 x=NULL)        # 階級値ベクトル
{
  PolyaEggenberger2 <- function(x,              # 確率変数
                                lambda,         # λ = n*p
                                r)              # r = n*δ
  {
    exp(                                        # 対数で計算して最後に逆対数をとる
      sum(sapply(0:(x-1), function(i) ifelse(i < 0, 0, log(1+i*r/lambda))))
      +x*log(lambda)
      -lgamma(x+1)
      +(-lambda/r-x)*log(1+r)
    )
  }
#===
  if (is.null(x)) {
    stop("関数の仕様が変更されました。度数ベクトルと同じ長さの階級値ベクトルも指定してください。")
  }
  if (length(x) != length(d)) {
    stop("度数ベクトル階級値ベクトルの長さは同じでなければなりません。")
  }
  data.name <- paste(deparse(substitute(d)), deparse(substitute(x)), sep=", ")
  method <- "ポリヤ・エッゲンベルガー分布への適合度の検定"

  o <- numeric(diff(range(x))+1)
  o[x-min(x)+1] <- d
  x <- min(x):max(x)

  k <- length(o)                                # 階級数
  n <- sum(o)                                   # データ数
  lambda <- sum(o*x)/n                          # 平均値（=λ）
  r <- sum(o*(x-lambda)^2)/n/lambda-1           # パラメータ r
  p <- sapply(x, PolyaEggenberger2, lambda, r)  # 確率
  if (min(x) != 0) {                            # 最初と最後の階級値の確率は階級値以下・以上の確率を併合する
    p[1] = sum(sapply(0:min(x), PolyaEggenberger2, lambda, r))
  }
  p[k] <- 1-sum(p[-k])                          # 最後の確率は合計が 1 になるように
  e <- n*p                                      # 期待値
  table <- data.frame(x, o, p, e)               # 結果をデータフレームにまとめる
  rownames(table) <- paste("c-", x, sep="")

  while (e[1] < 1) {                            # 1 未満のカテゴリーの併合
    o[2] <- o[2]+o[1]
    e[2] <- e[2]+e[1]
    o <- o[-1]
    e <- e[-1]
    k <- k-1
  }
  while (e[k] < 1) {                            # 1 未満のカテゴリーの併合
    o[k-1] <- o[k-1]+o[k]
    e[k-1] <- e[k-1]+e[k]
    o <- o[-k]
    e <- e[-k]
    k <- k-1
  }
  chisq <- sum((o-e)^2/e)                       # カイ二乗統計量
  df <- k-3                                     # 自由度
  p <- pchisq(chisq, df, lower.tail=FALSE)      # P 値
  names(chisq) <- "X-squared"
  names(df) <- "df"
  return(structure(list(statistic=chisq, parameter=df, p.value=p,
    estimate=c(n=n, lambda=lambda, r=r), method=method,
    data.name=data.name, table=table), class=c("htest", "PolyaEggenbergerdist")))
}
# summary メソッド
summary.PolyaEggenbergerdist <- function(obj,   # PolyaEggenbergerdist が返すオブジェクト
                                         digits=5)
{
  table <- obj$table
  colnames(table) <- c("階級", "度数", "確率", "期待値")
  cat("\n適合度\n\n")
  print(table, digits=digits, row.names=FALSE)
}
# plot メソッド
plot.PolyaEggenbergerdist <- function(obj,      # PolyaEggenbergerdist が返すオブジェクト
                                      ...)      # barplot へ渡す引数
{
  table <- obj$table
  nr <- nrow(table)
  pos <- barplot(table$o, space=0, ...)         # 観察度数を barplot で描く
  old <- par(xpd=TRUE)
  points(pos, table$e, pch=3)                   # 理論度数を，記号 + で示す
  text(pos, -strheight("H"), table$x)
  par(old)
}


使用例

> d <- c(27, 61, 77, 71, 54, 35, 20, 11, 6, 2, 1)
> x <- 0:10
> (a <- PolyaEggenbergerdist(d, x))

	ポリヤ・エッゲンベルガー分布への適合度の検定

data:  d, x
X-squared = 0.6248, df = 8, p-value = 0.9997
sample estimates:
          n      lambda           r 
365.0000000   2.9917808   0.2682924 

> summary(a)

適合度

 階級 度数      確率  期待値
    0   27 0.0706286 25.7794
    1   61 0.1666061 60.8112
    2   77 0.2141257 78.1559
    3   71 0.1985646 72.4761
    4   54 0.1486017 54.2396
    5   35 0.0952554 34.7682
    6   20 0.0542416 19.7982
    7   11 0.0281137 10.2615
    8    6 0.0134934  4.9251
    9    2 0.0060738  2.2170
   10    1 0.0042954  1.5678

> plot(a)



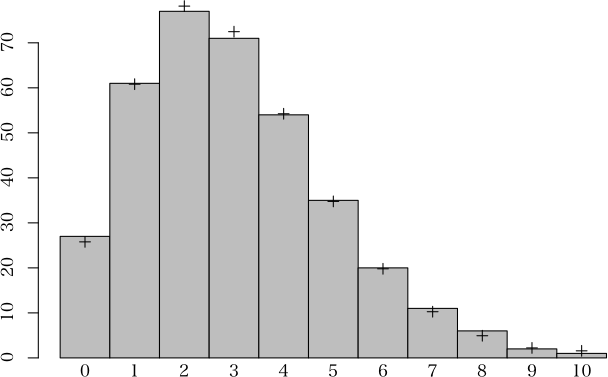> d <- c(1, 1, 3, 12, 27, 42, 63, 80, 108, 129, 108, 106, 87, 79, 45, 42, 31, 18, 8, 5, 1, 1, 2, 1)
> x <- 3:26
> (a <- PolyaEggenbergerdist(d, x))
ポリヤ・エッゲンベルガー分布への適合度の検定

データ:  d, x 
カイ二乗値 = 12.963, 自由度 = 19, P値 = 0.8405
標本推定値: 
            n        lambda             r 
1000.00000000   13.05000000   -0.09597701 

> summary(a)

適合度

 階級 度数       確率    期待値
    3    1 0.00067063   0.67063
    4    1 0.00190503   1.90503
    5    3 0.00533821   5.33821
    6   12 0.01237099  12.37099
    7   27 0.02438582  24.38582
    8   42 0.04173726  41.73726
    9   63 0.06300537  63.00537
   10   80 0.08493108  84.93108
   11  108 0.10325927 103.25927
   12  129 0.11416725 114.16725
   13  108 0.11558534 115.58534
   14  106 0.10778587 107.78587
   15   87 0.09304897  93.04897
   16   79 0.07468910  74.68910
   17   45 0.05595887  55.95887
   18   42 0.03926647  39.26647
   19   31 0.02588379  25.88379
   20   18 0.01607164  16.07164
   21    8 0.00942268   9.42268
   22    5 0.00522787   5.22787
   23    1 0.00275027   2.75027
   24    1 0.00137441   1.37441
   25    2 0.00065353   0.65353
   26    1 0.00051028   0.51028

 解説ページ