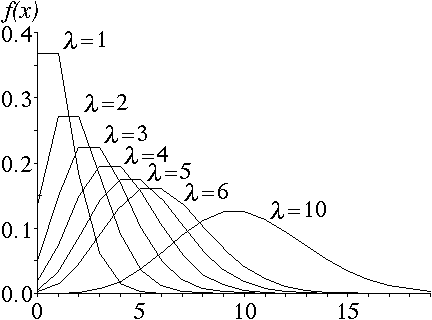
 図 1.ポアソン分布の概形 |
|---|
ポアソン分布の確率関数は次式で表される。 \[ f(x) = \frac{e^{-\lambda}\ \lambda^{x}} {x!},\ \lambda \gt 0,\ x = 0, 1, \dots \tag{1} \] ポアソン分布の概形は図 1 のようになるが,$\lambda$ が大きくなると正規分布に近づく(アニメーション,または,ムービー)。
 図 1.ポアソン分布の概形 |
|---|
二項分布において,生起確率 $p$ が極めて小さい場合がある。このとき,$n$ が十分に大きくても $n\ p$ は有限なものとなる。そこで,$n\ p = \lambda$ とおき,$n \rightarrow \infty$,$p \rightarrow 0$ としたとき,二項分布の( 1 )式の確率関数 $f ( x )$ を,$\lambda$ と $x$ を用いて表すことを考える。
$p = \lambda\ /\ n$ を二項分布の( 1 )式に代入すると,次式のようになる。 \begin{align*} f(x) & = \frac{n!}{x!\ (n-x)!}\ \left( \frac{\lambda}{n} \right)^x \left( 1-\frac{\lambda}{n} \right) ^{n-x} \\ & = \frac{\lambda^x}{x!}\ \left( 1-\frac{\lambda}{n} \right)^n \left( 1-\frac{\lambda}{n} \right)^{-x} \left( 1-\frac{1}{n} \right)\ \left( 1-\frac{2}{n} \right)\cdots \left( 1-\frac{x-1}{n} \right) \end{align*} ここで, \[ \lim_{n \rightarrow \infty} \left( 1-\frac{\lambda}{n} \right)^n = e^{-\lambda} \] および \[ \lim_{n \rightarrow \infty} \left( 1-\frac{\lambda}{n} \right)^{-x} \left( 1-\frac{1}{n} \right)\ \left( 1-\frac{2}{n} \right)\cdots \left( 1-\frac{x-1}{n} \right) = 1 \] に注意すると,( 1 )式になる。
ポアソン分布の平均 $E ( x )$ ,分散 $V ( x )$ は二項分布との関係より,
\[ E ( x ) = V ( x ) = \lambda \] である。
例題: 「自動車事故による死亡が 1 年間に 1 万人であるとする。日本の人口を 11,600 万人,ある都市の人口を 100 万人としたとき,その都市で自動車事故による死亡が一件もないという日が起こる確率を求めよ。」
解答: ある一人の人が交通事故にあう 1 日あたりの確率 $p$ はきわめて小さい。 \[ p = \frac{10000}{116000000\times 365} = 2.362 \times 10^{ - 7} \] また,この都市の人口はきわめて大きいので,交通事故死の確率はポアソン分布に従うと考えられる。
ポアソン分布のパラメータ $\lambda$ は, \[ \lambda = n\ p = 1000000\times 2.362 \times 10^{ - 7} = 0.2362 \] となる。
( 1 )式より,求める確率は $f ( 0 ) = 0.790$ となる。
このほか,ポアソン分布に当てはまる事象としては,製品中の不良品の個数,一定時間内に電話がかかってくる回数などがあげられる。
演習問題:
応用問題: