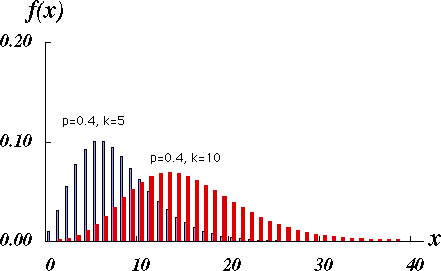
 図 1.負の二項分布の概形 |
|---|
ある実験を繰り返し行った場合,事象の起こる確率が $p$ であるならば,その事象の生起回数は 二項分布 に従った。
では,事象が $k$ 回起きるまで,何回その事象が起きなかったかを考えてみよう。
事象の起きなかった回数を $x$ とすると,それまでに $k - 1$ 回は事象が観察されるから,$n = k + x$ とすると,(1)式のようになる。この分布を負の二項分布と呼ぶ。 \[ f(x) = {x+k-1 \choose x} \ p^{k-1}\ q^x\ p = {n-1 \choose x} \ p^k\ q^x \tag{1} \] ただし,$p \gt 0,\ q \gt 0,\ p + q = 1,\ x = 0, 1, \dots$
 図 1.負の二項分布の概形 |
|---|
負の二項分布の平均 $E ( x )$ と分散 $V ( x )$ は
\[ E ( x ) = \frac{k\ q}{p},\ V ( x ) = \frac{k\ q}{p^{2}} \] である。
( 1 )式は,変形すると \[ f(k+x) = {n-1 \choose k-1} \ p^k\ q^x \] のようにも表すことができる。これは $n$ 回目にちょうど事象の生起回数が $k$ となった場合の確率を表す形である。
また,( 1 )式で $q^{x} = \left \{ - ( - q ) \right \}^{x} = ( - 1 ) ^{x} ( - q ) ^{x}$ であるから, \[ f(x) = {-k \choose x}\ p^k\ (-q)^x \tag{2} \] となる。ただし, \[ {-k \choose x} = \frac{(-k)\ (-k-1) \cdots \left \{ -k-(x-1)\right \}}{x!} = (-1)^x\ {x+k-1 \choose x} \] である。
( 2 )式において,注目している事象の起こらない回数 $x$ に負の項 $- k$ が対応している。これが負の二項分布と呼ばれる理由である。
演習問題:
応用問題: