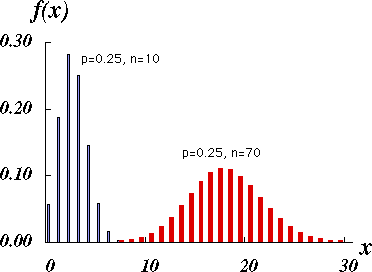
 図 1.二項分布の概形 |
|---|
ある集団において,特性 A を持つものの割合が $p$ であり,持たないものの割合が $q$ であるとする( $p + q = 1$ )。このとき,集団から無作為に $n$ 人を抽出したとき,特性 A を持つものが $x$ 人である確率を考える。$n$ 人のうち $x$ 人が特性を持つ組合せは ${}_{n}C_{x}$ 通りある( $\displaystyle {n \choose x}$ とも書く) 。その各々に対して,$x$ 人が特性 A を持つ確率は $p^{x}$,残り $n - x$ 人が特性を持たない確率は $q^{n - x}$ であり,両者が共に起こる確率は両者の積である。よって, \[ f(x) = {}_nC_{x}\ p^x\ q^{n-x},\ p \gt 0, q \gt 0,\ p+1=1,\ x=0, 1, \dots, n \] が求める確率であり,この分布を二項分布と呼ぶ。
$n$,$p$,$q$ は定数である。このようなパラメータのことを母数という。$n$,$p$ を与えることにより,この分布は確定する。$p$ を母比率という。この分布を $B ( n, p )$ と表すことにする。
図 1 は出現率が $0.25$ のとき,$n = 10$ と $n = 70$ について図示したものである。二項分布では $p = q = 0.5$ のときに左右対称な密度分布を持つが,$p$ と $q$ がかなり違う場合でも,$n$ が大きくなるにつれ,その形は次第に左右対称なもの(正規分布)に近づく(アニメーション,または,ムービー)。
 図 1.二項分布の概形 |
|---|
二項分布の平均 $E ( x )$ と分散 $V ( x )$ は \[ E ( x ) = n\ p,\ V ( x ) = n\ p\ q \] である。
ところで,1 回ごとの事象の生起確率 $p$ が一定であるとき,実験を繰り返し行うことを ベルヌーイ試行というが,独立に実験を $n$ 回繰り返したとき,$x$ 回事象が生じる確率は二項分布である。このため二項分布はベルヌーイ分布とも呼ばれる。
問題: 「生まれてくる子どもの性比を,男:女 = 22:21 としたとき,ある団地で 5 人の子どもが生まれるとして,そのうちの 4 人以上が男,あるいは,4 人以上が女である確率を求めよ。」
解答: 求めるのは,( 1 )式を用いて,
$f ( 0 ) + f ( 1 ) + f ( 4 ) + f ( 5 ) = 1 - \left \{ f ( 2 ) + f ( 3 ) \right \}$ である。
答えは,$0.37567586$。
演習問題−1:
「全製品のうち不良品が $1 / 6$ の割合で含まれている。いまこれら製品のうちから,$5$ 個を無作為に選んだとき,その中に不良品が $x$ 個だけ含まれる確率はいかほどか。その確率分布を示し,母平均,母分散を計算せよ。」
問題1 母比率はいくつか。答えを分数で解答欄に記入し,送信ボタンをクリックしなさい。
問題2 母平均を求めなさい。答えを分数で解答欄に記入し,送信ボタンをクリックしなさい。
問題3 母分散を求めなさい。答えを分数で解答欄に記入し,送信ボタンをクリックしなさい。
演習問題−2:
「$5$ 人兄弟の同胞 $100$ 組を選んで,これら各組ごとに男子の数を調べたところ,表 1 のようになった( 男子の数 $x$ と実測度数 $f_{i}$ の欄 )。このデータに対して,理論分布としての二項分布をあてはめなさい。」
| 男子の数 $x_{i}$ | 実測度数 $f_{i}$ | 相対度数 $f_{i}\ /\ 100$ |
|---|---|---|
| 0 | 2 | 0.02 |
| 1 | 14 | 0.14 |
| 2 | 20 | 0.20 |
| 3 | 34 | 0.34 |
| 4 | 22 | 0.22 |
| 5 | 8 | 0.08 |
| 計 | 100 | 1.00 |
応用問題:
「演習問題−1を積率母関数を用いて理論的に解いてみよう。」