No.20888 Re: 母集団が正規分布でないときのカイ二乗値の分布 【青木繁伸】 2014/02/21(Fri) 23:33
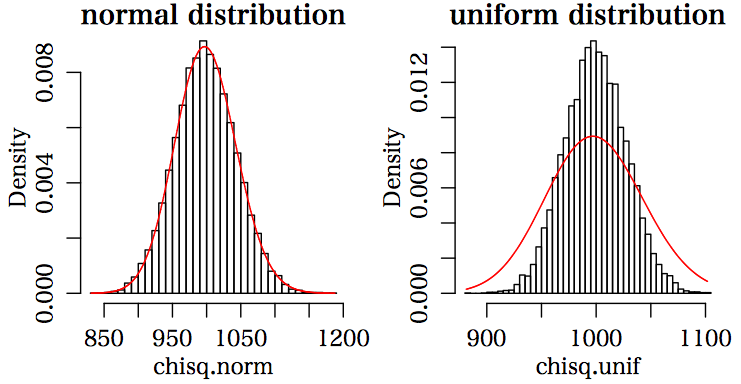
シミュレーションしましたが,母集団が一様分布などだと示された統計量はカイ二乗分布に従うとはいえませんね。下の図は,n=1000 の場合ですが,あきらかに違いますね。左は正規母集団,右は一様分布母集団の場合。
なお,
> データの分布の正規性を仮定できない場合でも,標本数が十分に大きければ,パラメトリックな分散分析を使ってもよいか
ということならば,一元配置分散分析ならば,等分散を仮定しない Welch の方法によればよいと思いますよ。R では,一元配置分散分析の場合も,等分散を仮定しない Welch の方法がデフォルトです。
trial <- 10000
n <- 1000
chisq.norm <- replicate(trial, {V <- 1; x <- rnorm(n); sum((x-mean(x))^2)/V})
chisq.unif <- replicate(trial, {V <- 1/12; x <- runif(n); sum((x-mean(x))^2)/V})
layout(matrix(1:2, 1))
old <- par(mar=c(3, 3, 1.2, 1), mgp=c(1.8, 0.8, 0))
hist(chisq.norm, breaks=50, probability=TRUE, main="normal distribution")
x <- seq(min(chisq.norm), max(chisq.norm), by=0.01)
lines(x, dchisq(x, n-1), col="red")
hist(chisq.unif, breaks=50, probability=TRUE, main="uniform distribution")
x <- seq(min(chisq.unif), max(chisq.unif), by=0.01)
lines(x, dchisq(x, n-1), col="red")
par(old)
layout(1)