二群の平均値(代表値)の差を検定するとき
First upload: Feb 02, 2007
Last modified: Feb 10, 2007
1. はじめに
二群の平均値(代表値)の差の検定をするときに,両群の分散が違うといろいろ問題が残る。
粕谷によれば,そのようなときには,分散の影響を受けない中央値検定を採用すればよいと書いてあるという情報・書き込みがいくつも現れる。
本当にそうだろうか。粕谷1)はそのように書いてあるのだろうか。
いろいろ検討してみたが,粕谷は「分散が等しくないから中央値検定」などと単純には言っていないようだし,その後の同じ学会誌に Markus Neuhäuser2) は別の提言をしている。
分散が等しくない場合の二群の代表値の差の検定に困難が伴うのは古くからの議論である。
しかし,だからといって,データ水準や検出力の面から考えて最低位に位置づけられれ中央値検定を採用すべしと言うのは,納得しがたい。
粕谷論文のフォローを検索し,いろいろやってみると,粕谷は必ずしもいつでも中央値検定をやれと言っているわけでもないし,粕谷が提唱している等分散性の検定を行ってから次の検定を決めようというのも問題のあることは明らかである。
分散が異なるデータは,マン・ホイットニーの U 検定などは行えない,中央値検定を行うべしというのは,粕谷も意図しない過剰反応ではないだろうか。
今回,そのような短絡的思考を検証するために,データの分布として3種をあげ,標準偏差の比が 0.25 〜 4 の範囲で,各種検定の第一種の過誤がどれくらいになるかを検討したので報告しておく。
2. 方法
標本サイズとしては,両群が等しい場合(n1=20, n2=20),約 1:2 の場合(n1=15, n2=25),1:3 の場合(n1=10, n2=30)の,3 通りを考察する。
分散の違いとしては,標準偏差の比が 1 〜 4 まで 0.2 刻み,およびその逆数の 31 種類を考察する。
データの分布としては,正規分布のような左右対称な分布(図1),対数正規分布のような歪みのある分布(図2),一様分布のような分布(図3)という,3 種類を考察した。
データ生成・シミュレーションは,R を用いて行った。データの分布型と標本サイズの設定ごとに,標準偏差の比の 31 通りにおいて,平均値は同じで標準偏差の異なるデータを生成し検定を行うことを 5000 回ずつ実施した。
シミュレーションプログラムのソース
===== begin =====
BF.sim <- function(type, n1=20, n2=20, sd2=1, loop=5000)
{
calc <- function(x1, x2, n1, n2)
{
# median test メディアン検定
md <- median(c(x1, x2))
r1 <- sum(x1 < md)
r2 <- sum(x2 < md)
tbl <- matrix(c(r1, r2, n1-r1, n2-r2), 2, 2)
chisq.n <- chisq.test(tbl, correct=FALSE)$p.value
chisq.c <- chisq.test(tbl, correct=TRUE)$p.value
fisher <- fisher.test(tbl)$p.value
# U test マン・ホイットニーの U 検定
U.n <- wilcox.test(x1, x2, correct=FALSE, exact=FALSE)$p.value
U.c <- wilcox.test(x1, x2, correct=TRUE, exact=FALSE)$p.value
# t test t 検定
t.w <- t.test(x1, x2, var.equal=FALSE)$p.value
t.n <- t.test(x1, x2, var.equal=TRUE)$p.value
# equality of valiance 等分散性の検定
vp <- var.test(x1, x2)$p.value # パラメトリック
an <- ansari.test(x1, x2)$p.value # ノンパラメトリック
return(c(
chisq.n=chisq.n, # 1 メディアン検定を カイ二乗検定で
chisq.c=chisq.c, # 2 メディアン検定を 連続性の補正をするカイ二乗検定検定で
fisher=fisher, # 3 メディアン検定を フィッシャーの正確検定で
U.n=U.n, # 4 マン・ホイットニーの U 検定
U.c=U.c, # 5 連続性の補正をするマン・ホイットニーの U 検定
t.w=t.w, # 6 ウエルチの方法による t 検定
t.n=t.n, # 7 普通の t 検定
vp=vp, # 8 等分散性の検定
an=an)) # 9 アンサリ検定
}
if (type == "normal") { # 正規分布
g1 <- matrix(rnorm(n1*loop, sd=1), loop, n1)
g2 <- matrix(rnorm(n2*loop, sd=sd2), loop, n2)
}
else if (type == "lognormal") { # 対数正規分布みたいな外形をした分布(平均値,標準偏差を調整する)
g1 <- matrix(scale(rlnorm(n1*loop, sdlog=0.4)), loop, n1)
g2 <- matrix(scale(rlnorm(n2*loop, sdlog=0.4))*sd2, loop, n2)
}
else if (type == "uniform") { # 一様分布
g1 <- matrix(scale(runif(n1*loop)), loop, n1)
g2 <- matrix(scale(runif(n2*loop))*sd2, loop, n2)
}
result <- t(sapply(1:loop, function(i) calc(g1[i,], g2[i,], n1, n2)))
return(result)
}
draw <- function(type, n1, n2, loop, result) # 結果を図にする
{
color <- c("", "red","magenta","orange","blue","purple","brown","grey1")
linetype <- c(4, 4, 1, 2, 3, 4, 1, 2, 3, 4)
rng <- range(as.vector(result[,2:8]))
pdf(paste(type, n1, n2, "pdf", sep="."), onefile=FALSE, width=800/72, height=600/72)
old <- par(mar=c(4,4,1,1), cex=2)
plot(c(1,31), rng, type="n", ylim=c(0, 0.25), xaxt="n", xlab="sd2 / sd1",
ylab="Type I error", main=paste(type, ", n1=", n1, ", n2=", n2, ", trial=", loop, sep=""))
sapply(2:8, function(i) lines(1:31, result[,i], col=color[i], lwd=4, lty=linetype[i]))
abline(h=0.05, v=16, lty=3, lwd=1)
legend(18, 0.25, c("chisq.test", "chisq.test(c)", "fisher.test", "wilcox.test",
"wilcox.test(c)", "t.test(w)", "t.test"), col=color[2:8], lwd=6)
axis(1, at=1:31, labels=c("1/4", "1/3.8", "1/3.6", "1/3.4", "1/3.2", "1/3",
"1/2.8", "1/2.6", "1/2.4", "1/2.2", "1/2", "1/1.8", "1/1.6", "1/1.4",
"1/1.2", "1", "1.2", "1.4", "1.6", "1.8", "2", "2.2", "2.4", "2.6",
"2.8", "3", "3.2", "3.4", "3.6", "3.8", "4"))
par(old)
dev.off()
}
driver2 <- function(type, n1, n2, sd2, loop)
{
result <- BF.sim(type, n1, n2, sd2, loop)
resultp <- result < 0.05
return(colSums(resultp)/loop)
}
driver <- function(type, n1, n2, sd2, loop=5000) # 分布の形,各群のサンプルサイズ,標準偏差の比
{
sink(paste(type, n1, n2, "log", sep="."))
cat("\n\nn1=", n1, " n2=", n2, " trial=", loop, " distribution=", type, "\n\n")
result <- t(sapply(sd2, function(sd2) c(sd2=sd2, driver2(type, n1, n2, sd2, loop))))
print(result)
draw(type, n1, n2, loop, result)
sink()
}
# 第二群の標準偏差のベクトル 1〜4 を 0.2 刻みで,逆方向も
sd2 <- seq(1, 4, by=0.2) # 大きくなる方
sd2 <- c(1/rev(sd2), sd2[-1]) # 小さくなる方
loop <- 50 # 試行回数
driver("normal", 5, 5, sd2, loop) # シミュレーション実行
===== end =====
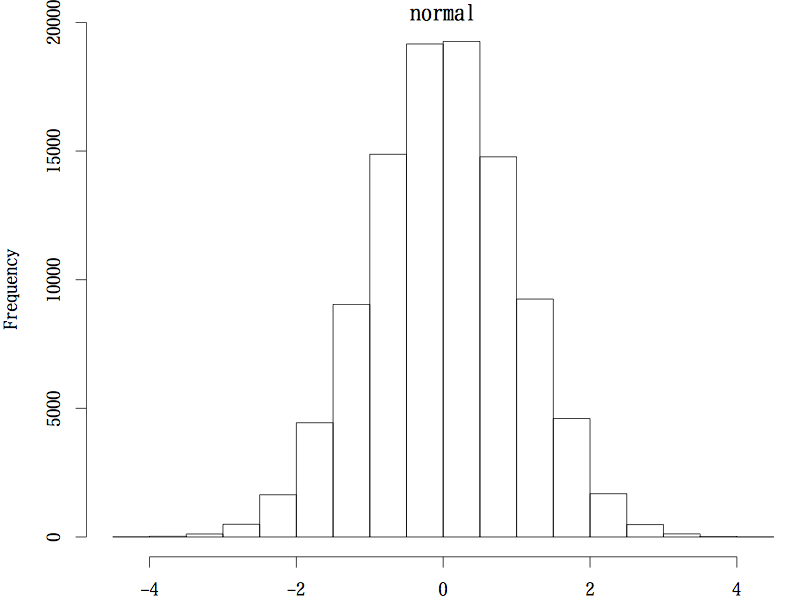
図1. 左右対称な分布 |
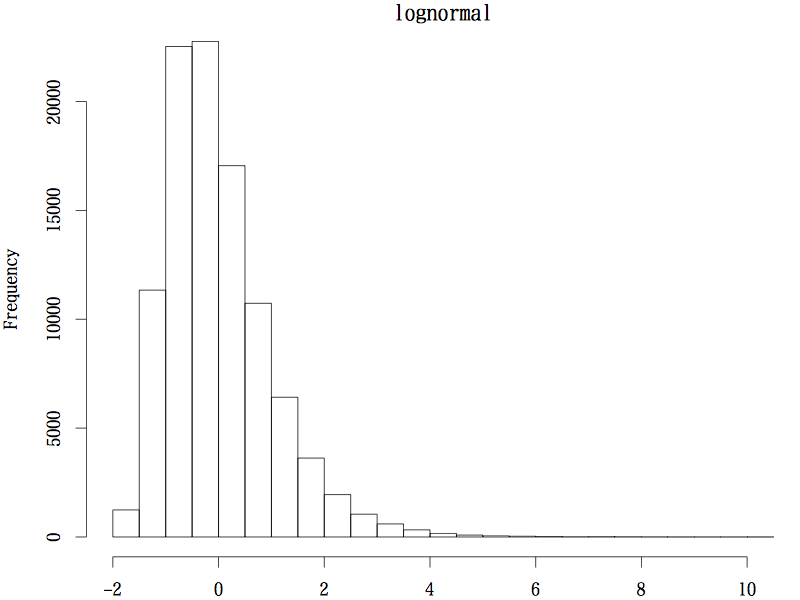
図2. 歪みのある分布 |
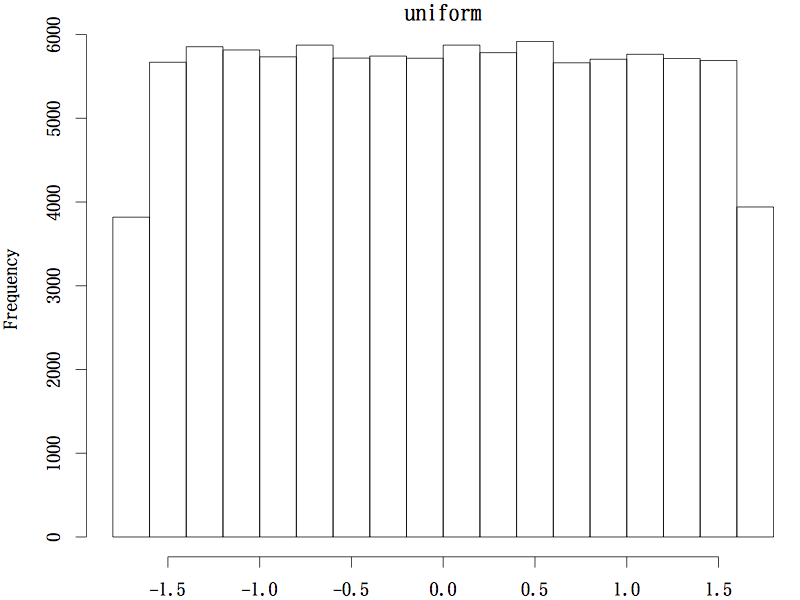
図3. 一様な分布 |
3. 結果
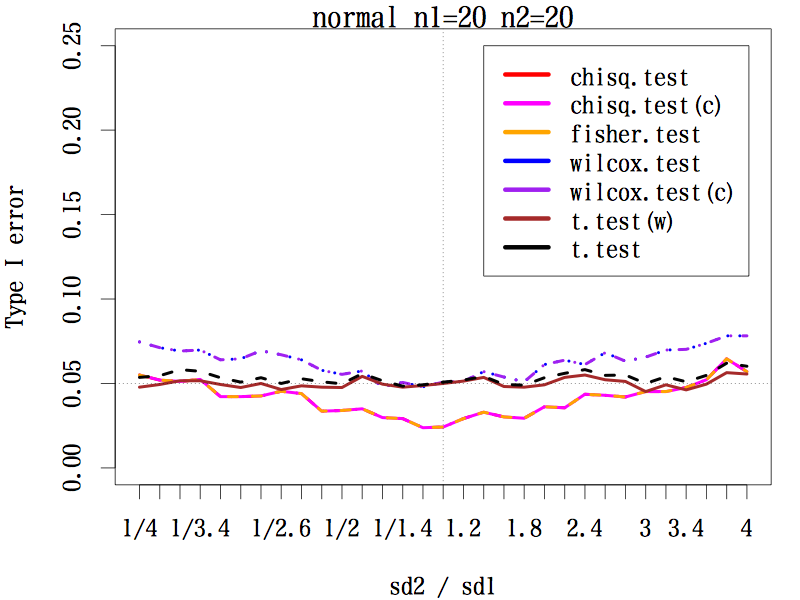
以下に示す図の,横軸は二群の標準偏差の比,縦軸は1000回の実験において,有意になった割合(第一種の誤差)である。この値が 0.05 であることが期待される。
chisq.test は中央値検定(カイ二乗検定),chisq.test(c) は連続性の補正をしたもの,fisher.test は中央値検定に使うクロス集計表に対して Fisher の正確検定を行った結果,wilcox.test はマン・ホイットニーの U 検定検定,wilcox.test(c) は連続性の補正をしたもの,t.test(w) は等分散を仮定しない t 検定(ウェルチの方法),t.test は等分散を仮定する t.test である。
参考:三群以上の比較の場合の結果
3.1. 左右対称な分布の場合
3.1.1. サンプルサイズが等しい場合(n1=20, n2=20)
どの検定手法でも第一種の過誤はほぼ 0.05 をキープしているが,標準偏差の比が 1/2 〜 2 のときの中央値検定は 0.05 よりかなり小さい。マン・ホイットニーの U 検定は,標準偏差の比に敏感なようである。
表の最後の二列は,等分散の検定と Ansari-Bradley 検定の第一種の過誤である。
 |
| 標準偏差の比 | chisq.test | chisq.test(c) | fisher.test | wilcox.test | wilcox.test(c) | t.test(w) | t.test | var.test | ansari.test |
| 0.2500 | 0.0550 | 0.0550 | 0.0550 | 0.0746 | 0.0746 | 0.0478 | 0.0536 | 1.0000 | 0.9770 |
| 0.2632 | 0.0520 | 0.0520 | 0.0520 | 0.0712 | 0.0712 | 0.0494 | 0.0546 | 0.9994 | 0.9712 |
| 0.2778 | 0.0512 | 0.0512 | 0.0512 | 0.0692 | 0.0692 | 0.0516 | 0.0582 | 0.9996 | 0.9644 |
| 0.2941 | 0.0524 | 0.0524 | 0.0524 | 0.0698 | 0.0698 | 0.0516 | 0.0572 | 0.9998 | 0.9486 |
| 0.3125 | 0.0422 | 0.0422 | 0.0422 | 0.0640 | 0.0640 | 0.0494 | 0.0534 | 0.9984 | 0.9204 |
| 0.3333 | 0.0422 | 0.0422 | 0.0422 | 0.0646 | 0.0646 | 0.0476 | 0.0508 | 0.9952 | 0.9084 |
| 0.3571 | 0.0426 | 0.0426 | 0.0426 | 0.0694 | 0.0694 | 0.0500 | 0.0534 | 0.9916 | 0.8736 |
| 0.3846 | 0.0454 | 0.0454 | 0.0454 | 0.0670 | 0.0670 | 0.0464 | 0.0500 | 0.9804 | 0.8228 |
| 0.4167 | 0.0440 | 0.0440 | 0.0440 | 0.0640 | 0.0640 | 0.0486 | 0.0528 | 0.9598 | 0.7578 |
| 0.4545 | 0.0336 | 0.0336 | 0.0336 | 0.0578 | 0.0578 | 0.0478 | 0.0510 | 0.9186 | 0.6820 |
| 0.5000 | 0.0340 | 0.0340 | 0.0340 | 0.0554 | 0.0554 | 0.0476 | 0.0498 | 0.8446 | 0.5862 |
| 0.5556 | 0.0350 | 0.0350 | 0.0350 | 0.0574 | 0.0574 | 0.0542 | 0.0558 | 0.7062 | 0.4578 |
| 0.6250 | 0.0298 | 0.0298 | 0.0298 | 0.0480 | 0.0480 | 0.0496 | 0.0516 | 0.5056 | 0.3122 |
| 0.7143 | 0.0292 | 0.0292 | 0.0292 | 0.0506 | 0.0506 | 0.0478 | 0.0484 | 0.2816 | 0.1844 |
| 0.8333 | 0.0238 | 0.0238 | 0.0238 | 0.0480 | 0.0480 | 0.0488 | 0.0492 | 0.1216 | 0.0930 |
| 1.0000 | 0.0242 | 0.0242 | 0.0242 | 0.0508 | 0.0508 | 0.0500 | 0.0508 | 0.0486 | 0.0482 |
| 1.2000 | 0.0292 | 0.0292 | 0.0292 | 0.0512 | 0.0512 | 0.0514 | 0.0520 | 0.1102 | 0.0852 |
| 1.4000 | 0.0330 | 0.0330 | 0.0330 | 0.0570 | 0.0570 | 0.0536 | 0.0542 | 0.2898 | 0.1828 |
| 1.6000 | 0.0302 | 0.0302 | 0.0302 | 0.0538 | 0.0538 | 0.0482 | 0.0494 | 0.5130 | 0.3214 |
| 1.8000 | 0.0294 | 0.0294 | 0.0294 | 0.0510 | 0.0510 | 0.0478 | 0.0490 | 0.7072 | 0.4616 |
| 2.0000 | 0.0362 | 0.0362 | 0.0362 | 0.0612 | 0.0612 | 0.0492 | 0.0534 | 0.8394 | 0.5804 |
| 2.2000 | 0.0356 | 0.0356 | 0.0356 | 0.0638 | 0.0638 | 0.0536 | 0.0560 | 0.9164 | 0.6832 |
| 2.4000 | 0.0436 | 0.0436 | 0.0436 | 0.0612 | 0.0612 | 0.0550 | 0.0582 | 0.9582 | 0.7652 |
| 2.6000 | 0.0430 | 0.0430 | 0.0430 | 0.0682 | 0.0682 | 0.0522 | 0.0548 | 0.9830 | 0.8178 |
| 2.8000 | 0.0420 | 0.0420 | 0.0420 | 0.0632 | 0.0632 | 0.0512 | 0.0550 | 0.9914 | 0.8654 |
| 3.0000 | 0.0452 | 0.0452 | 0.0452 | 0.0656 | 0.0656 | 0.0452 | 0.0500 | 0.9962 | 0.9024 |
| 3.2000 | 0.0452 | 0.0452 | 0.0452 | 0.0698 | 0.0698 | 0.0492 | 0.0540 | 0.9984 | 0.9322 |
| 3.4000 | 0.0476 | 0.0476 | 0.0476 | 0.0702 | 0.0702 | 0.0462 | 0.0510 | 0.9990 | 0.9478 |
| 3.6000 | 0.0522 | 0.0522 | 0.0522 | 0.0738 | 0.0738 | 0.0496 | 0.0548 | 1.0000 | 0.9592 |
| 3.8000 | 0.0646 | 0.0646 | 0.0646 | 0.0782 | 0.0782 | 0.0564 | 0.0620 | 0.9998 | 0.9670 |
| 4.0000 | 0.0570 | 0.0570 | 0.0570 | 0.0782 | 0.0782 | 0.0556 | 0.0602 | 0.9998 | 0.9746 |
3.1.2. サンプルサイズが約 1:2 の場合(n1=15, n2=25)
等分散を仮定する t 検定は等分散以外のときには第一種の過誤は 0.05 とはいえない。マン・ホイットニーの U 検定も程度は弱いが同じ傾向である。
ウェルチの方法による t 検定は,標準偏差の比がどのようであっても,第一種の過誤はほぼ 0.05 をキープしている。
連続性の補正をした中央値検定の第一種の過誤は低すぎ,補正をしない中央値検定はフィッシャーの正確検定と同じ動きをするが,標準偏差の比が偏っていると第一種の過誤は 0.05 より大きい。
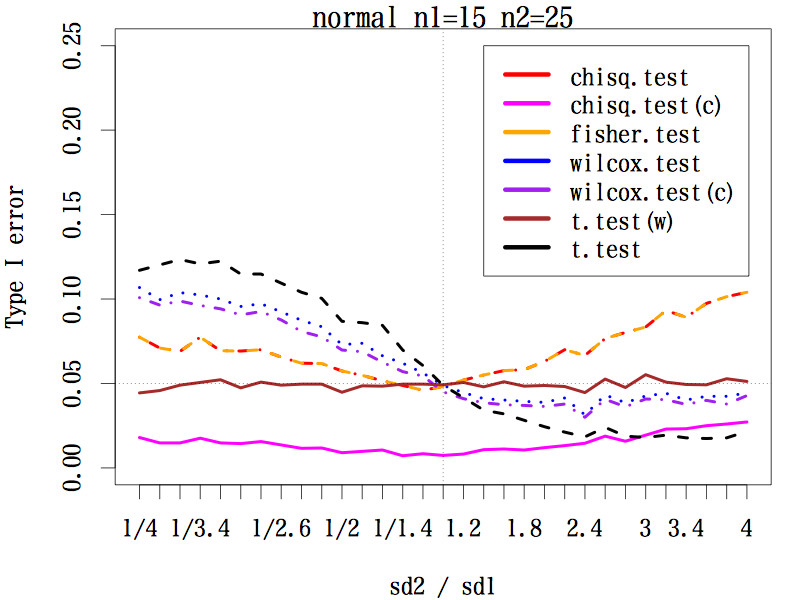 |
| 標準偏差の比 | chisq.test | chisq.test(c) | fisher.test | wilcox.test | wilcox.test(c) | t.test(w) | t.test | var.test | ansari.test |
| 0.2500 | 0.0774 | 0.0180 | 0.0774 | 0.1068 | 0.1008 | 0.0444 | 0.1170 | 0.9998 | 0.9636 |
| 0.2632 | 0.0710 | 0.0148 | 0.0710 | 0.0996 | 0.0964 | 0.0458 | 0.1202 | 0.9994 | 0.9630 |
| 0.2778 | 0.0690 | 0.0148 | 0.0690 | 0.1038 | 0.0988 | 0.0490 | 0.1234 | 0.9990 | 0.9406 |
| 0.2941 | 0.0774 | 0.0176 | 0.0774 | 0.1024 | 0.0962 | 0.0506 | 0.1208 | 0.9990 | 0.9224 |
| 0.3125 | 0.0694 | 0.0148 | 0.0694 | 0.1000 | 0.0942 | 0.0522 | 0.1224 | 0.9968 | 0.9082 |
| 0.3333 | 0.0692 | 0.0144 | 0.0692 | 0.0956 | 0.0906 | 0.0474 | 0.1148 | 0.9916 | 0.8850 |
| 0.3571 | 0.0700 | 0.0156 | 0.0700 | 0.0972 | 0.0926 | 0.0508 | 0.1148 | 0.9872 | 0.8454 |
| 0.3846 | 0.0656 | 0.0136 | 0.0656 | 0.0924 | 0.0876 | 0.0490 | 0.1094 | 0.9724 | 0.8054 |
| 0.4167 | 0.0620 | 0.0116 | 0.0620 | 0.0874 | 0.0808 | 0.0496 | 0.1040 | 0.9498 | 0.7258 |
| 0.4545 | 0.0618 | 0.0118 | 0.0618 | 0.0836 | 0.0776 | 0.0496 | 0.1004 | 0.9020 | 0.6634 |
| 0.5000 | 0.0574 | 0.0090 | 0.0574 | 0.0730 | 0.0698 | 0.0448 | 0.0868 | 0.8286 | 0.5708 |
| 0.5556 | 0.0548 | 0.0098 | 0.0548 | 0.0738 | 0.0688 | 0.0486 | 0.0860 | 0.7044 | 0.4404 |
| 0.6250 | 0.0516 | 0.0106 | 0.0516 | 0.0664 | 0.0626 | 0.0484 | 0.0844 | 0.5146 | 0.3182 |
| 0.7143 | 0.0488 | 0.0072 | 0.0488 | 0.0620 | 0.0570 | 0.0496 | 0.0698 | 0.3016 | 0.1888 |
| 0.8333 | 0.0460 | 0.0084 | 0.0460 | 0.0562 | 0.0544 | 0.0496 | 0.0606 | 0.1200 | 0.0892 |
| 1.0000 | 0.0482 | 0.0074 | 0.0482 | 0.0488 | 0.0450 | 0.0492 | 0.0488 | 0.0480 | 0.0484 |
| 1.2000 | 0.0520 | 0.0082 | 0.0520 | 0.0446 | 0.0410 | 0.0506 | 0.0416 | 0.1058 | 0.0880 |
| 1.4000 | 0.0550 | 0.0108 | 0.0550 | 0.0410 | 0.0386 | 0.0480 | 0.0342 | 0.2498 | 0.1800 |
| 1.6000 | 0.0576 | 0.0112 | 0.0576 | 0.0402 | 0.0374 | 0.0510 | 0.0320 | 0.4538 | 0.3032 |
| 1.8000 | 0.0582 | 0.0106 | 0.0582 | 0.0394 | 0.0370 | 0.0484 | 0.0282 | 0.6338 | 0.4310 |
| 2.0000 | 0.0630 | 0.0120 | 0.0630 | 0.0388 | 0.0364 | 0.0488 | 0.0244 | 0.7820 | 0.5492 |
| 2.2000 | 0.0700 | 0.0132 | 0.0700 | 0.0414 | 0.0378 | 0.0482 | 0.0212 | 0.8854 | 0.6664 |
| 2.4000 | 0.0666 | 0.0146 | 0.0666 | 0.0314 | 0.0300 | 0.0446 | 0.0184 | 0.9430 | 0.7458 |
| 2.6000 | 0.0766 | 0.0188 | 0.0766 | 0.0432 | 0.0406 | 0.0526 | 0.0240 | 0.9740 | 0.8154 |
| 2.8000 | 0.0802 | 0.0158 | 0.0802 | 0.0386 | 0.0362 | 0.0476 | 0.0188 | 0.9896 | 0.8572 |
| 3.0000 | 0.0834 | 0.0194 | 0.0834 | 0.0426 | 0.0408 | 0.0552 | 0.0180 | 0.9954 | 0.8988 |
| 3.2000 | 0.0932 | 0.0230 | 0.0932 | 0.0442 | 0.0404 | 0.0508 | 0.0194 | 0.9986 | 0.9240 |
| 3.4000 | 0.0892 | 0.0232 | 0.0892 | 0.0402 | 0.0376 | 0.0494 | 0.0178 | 0.9984 | 0.9390 |
| 3.6000 | 0.0974 | 0.0250 | 0.0974 | 0.0424 | 0.0400 | 0.0492 | 0.0174 | 0.9986 | 0.9508 |
| 3.8000 | 0.1014 | 0.0260 | 0.1014 | 0.0424 | 0.0378 | 0.0528 | 0.0178 | 1.0000 | 0.9680 |
| 4.0000 | 0.1040 | 0.0272 | 0.1040 | 0.0444 | 0.0428 | 0.0512 | 0.0216 | 0.9998 | 0.9708 |
3.1.3. サンプルサイズが 1:3 の場合(n1=10, n2=30)
等分散を仮定する t 検定は破滅的である。マン・ホイットニーの U 検定も程度は弱いが同じ傾向である。
連続性の補正をする中央値検定とフィッシャーの正確検定は全般的に第一種の過誤は 0.05 よりかなり低い。一方,連続性の補正をしない中央値検定の第一種の過誤はかなり高いレベルにある。
ウェルチの方法による t 検定は,標準偏差の比がどのようであっても,第一種の過誤はほぼ 0.05 をキープしている。
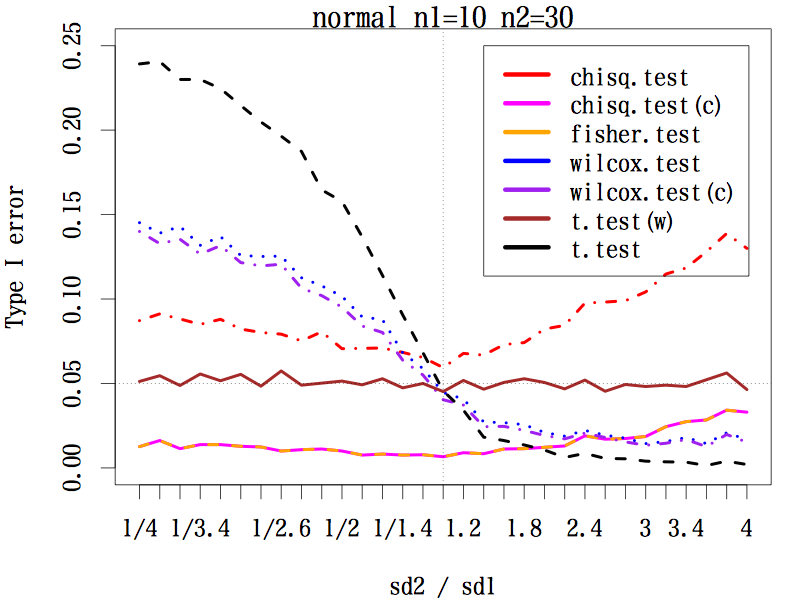 |
| 標準偏差の比 | chisq.test | chisq.test(c) | fisher.test | wilcox.test | wilcox.test(c) | t.test(w) | t.test | var.test | ansari.test |
| 0.2500 | 0.0872 | 0.0126 | 0.0126 | 0.1452 | 0.1400 | 0.0512 | 0.2392 | 0.9958 | 0.9104 |
| 0.2632 | 0.0912 | 0.0162 | 0.0162 | 0.1390 | 0.1328 | 0.0546 | 0.2406 | 0.9954 | 0.8906 |
| 0.2778 | 0.0882 | 0.0114 | 0.0114 | 0.1430 | 0.1354 | 0.0488 | 0.2300 | 0.9916 | 0.8776 |
| 0.2941 | 0.0850 | 0.0138 | 0.0138 | 0.1318 | 0.1266 | 0.0556 | 0.2300 | 0.9884 | 0.8458 |
| 0.3125 | 0.0880 | 0.0138 | 0.0138 | 0.1370 | 0.1316 | 0.0516 | 0.2246 | 0.9826 | 0.8284 |
| 0.3333 | 0.0822 | 0.0128 | 0.0128 | 0.1258 | 0.1216 | 0.0554 | 0.2146 | 0.9708 | 0.7944 |
| 0.3571 | 0.0802 | 0.0124 | 0.0124 | 0.1252 | 0.1196 | 0.0484 | 0.2048 | 0.9580 | 0.7540 |
| 0.3846 | 0.0792 | 0.0100 | 0.0100 | 0.1254 | 0.1206 | 0.0574 | 0.1964 | 0.9370 | 0.6928 |
| 0.4167 | 0.0752 | 0.0108 | 0.0108 | 0.1126 | 0.1064 | 0.0490 | 0.1874 | 0.8836 | 0.6332 |
| 0.4545 | 0.0806 | 0.0112 | 0.0112 | 0.1078 | 0.1020 | 0.0502 | 0.1646 | 0.8294 | 0.5610 |
| 0.5000 | 0.0706 | 0.0100 | 0.0100 | 0.1016 | 0.0952 | 0.0514 | 0.1578 | 0.7516 | 0.4778 |
| 0.5556 | 0.0708 | 0.0076 | 0.0076 | 0.0894 | 0.0840 | 0.0492 | 0.1368 | 0.6178 | 0.3632 |
| 0.6250 | 0.0710 | 0.0082 | 0.0082 | 0.0878 | 0.0802 | 0.0528 | 0.1140 | 0.4570 | 0.2668 |
| 0.7143 | 0.0684 | 0.0076 | 0.0076 | 0.0682 | 0.0638 | 0.0474 | 0.0906 | 0.2656 | 0.1642 |
| 0.8333 | 0.0654 | 0.0078 | 0.0078 | 0.0588 | 0.0550 | 0.0500 | 0.0682 | 0.1220 | 0.0904 |
| 1.0000 | 0.0594 | 0.0066 | 0.0066 | 0.0446 | 0.0404 | 0.0452 | 0.0456 | 0.0480 | 0.0486 |
| 1.2000 | 0.0678 | 0.0090 | 0.0090 | 0.0408 | 0.0372 | 0.0518 | 0.0342 | 0.0846 | 0.0692 |
| 1.4000 | 0.0668 | 0.0084 | 0.0084 | 0.0272 | 0.0244 | 0.0466 | 0.0182 | 0.1698 | 0.1388 |
| 1.6000 | 0.0730 | 0.0112 | 0.0112 | 0.0268 | 0.0246 | 0.0506 | 0.0162 | 0.3072 | 0.2318 |
| 1.8000 | 0.0742 | 0.0114 | 0.0114 | 0.0256 | 0.0222 | 0.0528 | 0.0136 | 0.4582 | 0.3334 |
| 2.0000 | 0.0822 | 0.0122 | 0.0122 | 0.0210 | 0.0192 | 0.0506 | 0.0106 | 0.6222 | 0.4576 |
| 2.2000 | 0.0844 | 0.0130 | 0.0130 | 0.0188 | 0.0172 | 0.0468 | 0.0062 | 0.7570 | 0.5514 |
| 2.4000 | 0.0976 | 0.0190 | 0.0190 | 0.0222 | 0.0206 | 0.0520 | 0.0086 | 0.8364 | 0.6440 |
| 2.6000 | 0.0982 | 0.0170 | 0.0170 | 0.0194 | 0.0180 | 0.0454 | 0.0056 | 0.9112 | 0.7166 |
| 2.8000 | 0.0990 | 0.0174 | 0.0174 | 0.0176 | 0.0154 | 0.0494 | 0.0054 | 0.9476 | 0.7732 |
| 3.0000 | 0.1042 | 0.0186 | 0.0186 | 0.0144 | 0.0134 | 0.0482 | 0.0040 | 0.9728 | 0.8266 |
| 3.2000 | 0.1148 | 0.0244 | 0.0244 | 0.0156 | 0.0146 | 0.0490 | 0.0036 | 0.9840 | 0.8556 |
| 3.4000 | 0.1184 | 0.0274 | 0.0274 | 0.0180 | 0.0168 | 0.0482 | 0.0034 | 0.9920 | 0.8806 |
| 3.6000 | 0.1280 | 0.0284 | 0.0284 | 0.0144 | 0.0126 | 0.0522 | 0.0014 | 0.9968 | 0.9086 |
| 3.8000 | 0.1388 | 0.0342 | 0.0342 | 0.0208 | 0.0198 | 0.0562 | 0.0040 | 0.9980 | 0.9270 |
| 4.0000 | 0.1300 | 0.0330 | 0.0330 | 0.0168 | 0.0152 | 0.0464 | 0.0020 | 0.9986 | 0.9378 |
3.2. 歪みのある分布の場合
3.2.1. サンプルサイズが等しい場合(n1=20, n2=20)
中央値検定は標準偏差の比が 1/3〜3 のあたりでは第一種の過誤は相当小さい。
標準偏差の比が 3.5 以上では,いずれの検定法でも第一種の過誤が0.5 より大きくなる。
ウェルチの方法による t 検定と普通の t 検定は,標準偏差の比がどのようであっても,第一種の過誤はほぼ 0.05 をキープしている。
マン・ホイットニーの U 検定は標準偏差の比が少しでも 1 からずれると,第一種の過誤はかなり大きくなる。
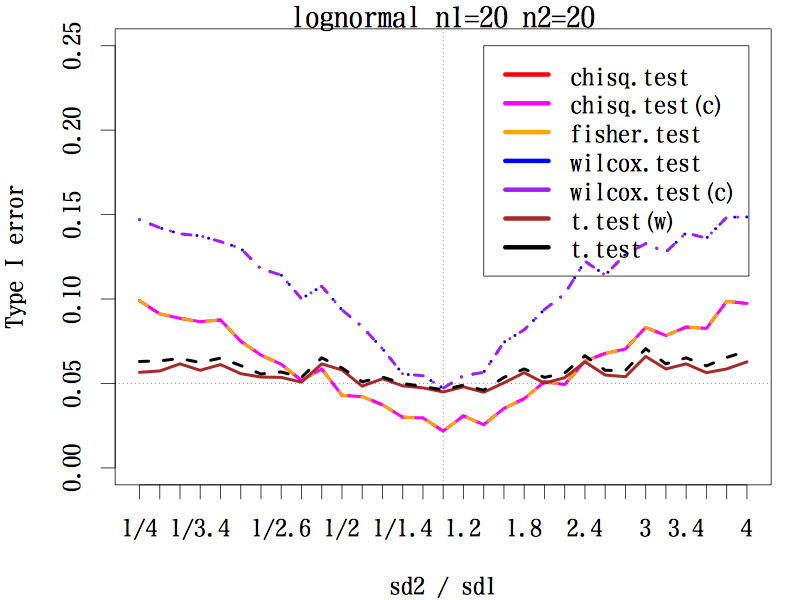 |
| 標準偏差の比 | chisq.test | chisq.test(c) | fisher.test | wilcox.test | wilcox.test(c) | t.test(w) | t.test | var.test | ansari.test |
| 0.2500 | 0.0990 | 0.0990 | 0.0990 | 0.1470 | 0.1470 | 0.0566 | 0.0630 | 0.9968 | 0.9768 |
| 0.2632 | 0.0912 | 0.0912 | 0.0912 | 0.1422 | 0.1422 | 0.0574 | 0.0634 | 0.9950 | 0.9728 |
| 0.2778 | 0.0886 | 0.0886 | 0.0886 | 0.1386 | 0.1386 | 0.0616 | 0.0648 | 0.9940 | 0.9660 |
| 0.2941 | 0.0866 | 0.0866 | 0.0866 | 0.1374 | 0.1374 | 0.0578 | 0.0624 | 0.9874 | 0.9600 |
| 0.3125 | 0.0876 | 0.0876 | 0.0876 | 0.1340 | 0.1340 | 0.0612 | 0.0650 | 0.9814 | 0.9426 |
| 0.3333 | 0.0750 | 0.0750 | 0.0750 | 0.1300 | 0.1300 | 0.0558 | 0.0606 | 0.9720 | 0.9216 |
| 0.3571 | 0.0668 | 0.0668 | 0.0668 | 0.1178 | 0.1178 | 0.0538 | 0.0556 | 0.9560 | 0.8986 |
| 0.3846 | 0.0614 | 0.0614 | 0.0614 | 0.1142 | 0.1142 | 0.0536 | 0.0568 | 0.9298 | 0.8574 |
| 0.4167 | 0.0518 | 0.0518 | 0.0518 | 0.1002 | 0.1002 | 0.0508 | 0.0536 | 0.8962 | 0.8122 |
| 0.4545 | 0.0586 | 0.0586 | 0.0586 | 0.1076 | 0.1076 | 0.0616 | 0.0652 | 0.8344 | 0.7254 |
| 0.5000 | 0.0430 | 0.0430 | 0.0430 | 0.0936 | 0.0936 | 0.0580 | 0.0592 | 0.7594 | 0.6284 |
| 0.5556 | 0.0422 | 0.0422 | 0.0422 | 0.0836 | 0.0836 | 0.0484 | 0.0510 | 0.6454 | 0.5120 |
| 0.6250 | 0.0374 | 0.0374 | 0.0374 | 0.0706 | 0.0706 | 0.0528 | 0.0538 | 0.5146 | 0.3606 |
| 0.7143 | 0.0300 | 0.0300 | 0.0300 | 0.0556 | 0.0556 | 0.0486 | 0.0500 | 0.3520 | 0.2206 |
| 0.8333 | 0.0296 | 0.0296 | 0.0296 | 0.0546 | 0.0546 | 0.0474 | 0.0482 | 0.2350 | 0.0984 |
| 1.0000 | 0.0218 | 0.0218 | 0.0218 | 0.0472 | 0.0472 | 0.0450 | 0.0462 | 0.1600 | 0.0440 |
| 1.2000 | 0.0308 | 0.0308 | 0.0308 | 0.0546 | 0.0546 | 0.0480 | 0.0490 | 0.2186 | 0.0938 |
| 1.4000 | 0.0256 | 0.0256 | 0.0256 | 0.0566 | 0.0566 | 0.0448 | 0.0460 | 0.3534 | 0.2088 |
| 1.6000 | 0.0352 | 0.0352 | 0.0352 | 0.0744 | 0.0744 | 0.0504 | 0.0536 | 0.5070 | 0.3634 |
| 1.8000 | 0.0410 | 0.0410 | 0.0410 | 0.0818 | 0.0818 | 0.0564 | 0.0586 | 0.6444 | 0.5140 |
| 2.0000 | 0.0510 | 0.0510 | 0.0510 | 0.0938 | 0.0938 | 0.0502 | 0.0536 | 0.7568 | 0.6386 |
| 2.2000 | 0.0494 | 0.0494 | 0.0494 | 0.1030 | 0.1030 | 0.0534 | 0.0562 | 0.8374 | 0.7340 |
| 2.4000 | 0.0632 | 0.0632 | 0.0632 | 0.1224 | 0.1224 | 0.0628 | 0.0664 | 0.8874 | 0.8052 |
| 2.6000 | 0.0678 | 0.0678 | 0.0678 | 0.1142 | 0.1142 | 0.0550 | 0.0578 | 0.9344 | 0.8542 |
| 2.8000 | 0.0704 | 0.0704 | 0.0704 | 0.1264 | 0.1264 | 0.0540 | 0.0576 | 0.9560 | 0.8984 |
| 3.0000 | 0.0832 | 0.0832 | 0.0832 | 0.1328 | 0.1328 | 0.0660 | 0.0706 | 0.9678 | 0.9216 |
| 3.2000 | 0.0784 | 0.0784 | 0.0784 | 0.1278 | 0.1278 | 0.0586 | 0.0616 | 0.9808 | 0.9466 |
| 3.4000 | 0.0834 | 0.0834 | 0.0834 | 0.1392 | 0.1392 | 0.0616 | 0.0652 | 0.9896 | 0.9536 |
| 3.6000 | 0.0826 | 0.0826 | 0.0826 | 0.1360 | 0.1360 | 0.0564 | 0.0604 | 0.9954 | 0.9648 |
| 3.8000 | 0.0986 | 0.0986 | 0.0986 | 0.1484 | 0.1484 | 0.0586 | 0.0654 | 0.9956 | 0.9722 |
| 4.0000 | 0.0974 | 0.0974 | 0.0974 | 0.1486 | 0.1486 | 0.0628 | 0.0692 | 0.9960 | 0.9804 |
3.2.2. サンプルサイズが約 1:2 の場合(n1=15, n2=25)
ウェルチの方法による t 検定は,標準偏差の比がどのようであっても,第一種の過誤はほぼ 0.05 をキープしている。
連続性の補正をした中央値検定は標準偏差の比が 1/4〜2.5 のあたりでは第一種の過誤は相当小さい。一方,連続性の補正をしない中央値検定とフィッシャーの正確検定は同じ動きをしているが,標準偏差の比が 1 以外の場合に 0.05 をかなり超えている。
マン・ホイットニーの U 検定も,標準偏差の比が 1 から離れると第一種の過誤はかなり大きい。
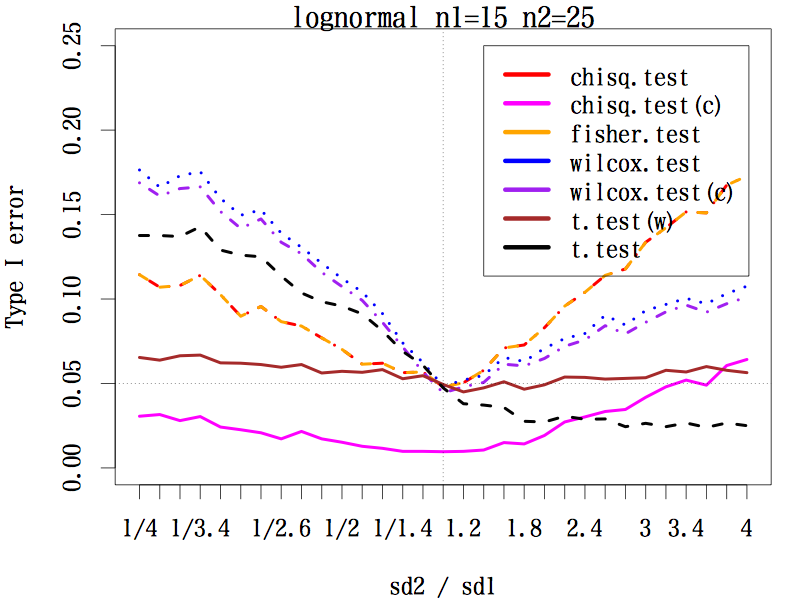 |
| 標準偏差の比 | chisq.test | chisq.test(c) | fisher.test | wilcox.test | wilcox.test(c) | t.test(w) | t.test | var.test | ansari.test |
| 0.2500 | 0.1144 | 0.0306 | 0.1144 | 0.1764 | 0.1688 | 0.0654 | 0.1376 | 0.9952 | 0.9704 |
| 0.2632 | 0.1070 | 0.0316 | 0.1070 | 0.1662 | 0.1610 | 0.0638 | 0.1376 | 0.9944 | 0.9644 |
| 0.2778 | 0.1080 | 0.0280 | 0.1080 | 0.1730 | 0.1654 | 0.0664 | 0.1370 | 0.9904 | 0.9562 |
| 0.2941 | 0.1140 | 0.0304 | 0.1140 | 0.1754 | 0.1664 | 0.0668 | 0.1428 | 0.9844 | 0.9450 |
| 0.3125 | 0.1026 | 0.0242 | 0.1026 | 0.1596 | 0.1518 | 0.0622 | 0.1290 | 0.9764 | 0.9224 |
| 0.3333 | 0.0898 | 0.0226 | 0.0898 | 0.1496 | 0.1418 | 0.0620 | 0.1260 | 0.9652 | 0.8998 |
| 0.3571 | 0.0956 | 0.0208 | 0.0956 | 0.1528 | 0.1474 | 0.0612 | 0.1250 | 0.9468 | 0.8750 |
| 0.3846 | 0.0866 | 0.0172 | 0.0866 | 0.1390 | 0.1336 | 0.0596 | 0.1136 | 0.9186 | 0.8338 |
| 0.4167 | 0.0840 | 0.0216 | 0.0840 | 0.1306 | 0.1268 | 0.0612 | 0.1036 | 0.8710 | 0.7810 |
| 0.4545 | 0.0770 | 0.0172 | 0.0770 | 0.1212 | 0.1158 | 0.0562 | 0.0984 | 0.8250 | 0.7090 |
| 0.5000 | 0.0702 | 0.0152 | 0.0702 | 0.1122 | 0.1074 | 0.0572 | 0.0958 | 0.7298 | 0.6178 |
| 0.5556 | 0.0614 | 0.0128 | 0.0614 | 0.1042 | 0.0992 | 0.0566 | 0.0912 | 0.6274 | 0.5050 |
| 0.6250 | 0.0620 | 0.0116 | 0.0620 | 0.0914 | 0.0862 | 0.0582 | 0.0812 | 0.4898 | 0.3638 |
| 0.7143 | 0.0564 | 0.0098 | 0.0564 | 0.0740 | 0.0716 | 0.0528 | 0.0690 | 0.3448 | 0.2134 |
| 0.8333 | 0.0568 | 0.0098 | 0.0568 | 0.0624 | 0.0568 | 0.0546 | 0.0608 | 0.2200 | 0.0948 |
| 1.0000 | 0.0480 | 0.0096 | 0.0480 | 0.0484 | 0.0444 | 0.0494 | 0.0474 | 0.1664 | 0.0498 |
| 1.2000 | 0.0504 | 0.0098 | 0.0504 | 0.0520 | 0.0480 | 0.0450 | 0.0380 | 0.2248 | 0.0902 |
| 1.4000 | 0.0578 | 0.0106 | 0.0578 | 0.0548 | 0.0506 | 0.0474 | 0.0372 | 0.3446 | 0.2066 |
| 1.6000 | 0.0710 | 0.0150 | 0.0710 | 0.0654 | 0.0614 | 0.0510 | 0.0358 | 0.4872 | 0.3576 |
| 1.8000 | 0.0728 | 0.0142 | 0.0728 | 0.0630 | 0.0604 | 0.0466 | 0.0276 | 0.6248 | 0.4928 |
| 2.0000 | 0.0830 | 0.0192 | 0.0830 | 0.0708 | 0.0648 | 0.0492 | 0.0272 | 0.7318 | 0.6082 |
| 2.2000 | 0.0958 | 0.0272 | 0.0958 | 0.0766 | 0.0720 | 0.0538 | 0.0306 | 0.8102 | 0.7068 |
| 2.4000 | 0.1040 | 0.0302 | 0.1040 | 0.0796 | 0.0758 | 0.0536 | 0.0288 | 0.8682 | 0.7810 |
| 2.6000 | 0.1140 | 0.0334 | 0.1140 | 0.0904 | 0.0842 | 0.0526 | 0.0290 | 0.9206 | 0.8378 |
| 2.8000 | 0.1178 | 0.0346 | 0.1178 | 0.0846 | 0.0794 | 0.0530 | 0.0244 | 0.9486 | 0.8822 |
| 3.0000 | 0.1336 | 0.0418 | 0.1336 | 0.0932 | 0.0862 | 0.0534 | 0.0264 | 0.9626 | 0.9124 |
| 3.2000 | 0.1422 | 0.0480 | 0.1422 | 0.0968 | 0.0924 | 0.0578 | 0.0244 | 0.9770 | 0.9272 |
| 3.4000 | 0.1516 | 0.0520 | 0.1516 | 0.1004 | 0.0964 | 0.0568 | 0.0266 | 0.9852 | 0.9428 |
| 3.6000 | 0.1510 | 0.0490 | 0.1510 | 0.0972 | 0.0922 | 0.0600 | 0.0240 | 0.9880 | 0.9568 |
| 3.8000 | 0.1674 | 0.0606 | 0.1674 | 0.1032 | 0.0972 | 0.0578 | 0.0266 | 0.9922 | 0.9644 |
| 4.0000 | 0.1728 | 0.0642 | 0.1728 | 0.1076 | 0.1012 | 0.0564 | 0.0250 | 0.9944 | 0.9728 |
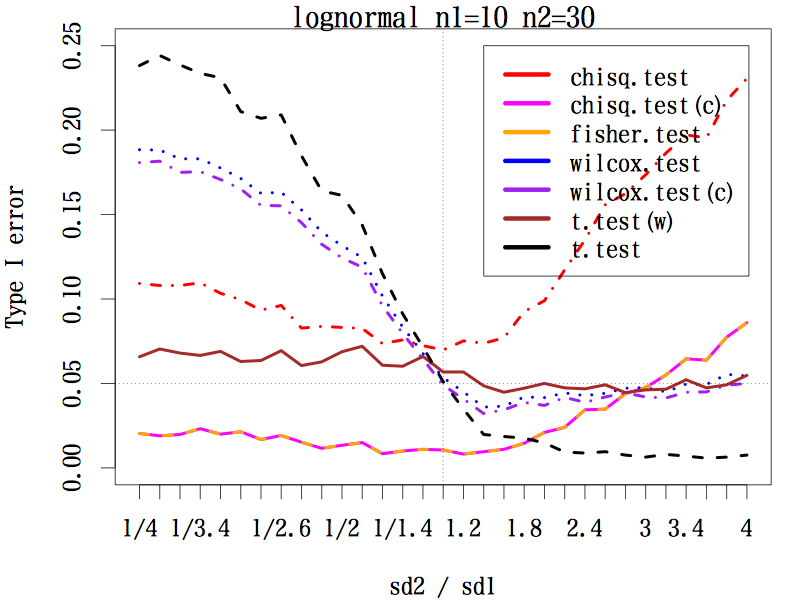
3.2.3. サンプルサイズが 1:3 の場合(n1=10, n2=30)
等分散を仮定する t 検定は破滅的である。マン・ホイットニーの U 検定も程度は弱いが同じ傾向である。
連続性の補正をした中央値検定とフィッシャーの正確検定は同じ動きをするが,全般的に第一種の過誤は 0.05 よりかなり低い。逆に,連続性の補正をしない中央値検定ではかなり大きい。
ウェルチの方法による t 検定は,標準偏差の比がどのようであっても,第一種の過誤はほぼ 0.05 をキープしている。
 |
| 標準偏差の比 | chisq.test | chisq.test(c) | fisher.test | wilcox.test | wilcox.test(c) | t.test(w) | t.test | var.test | ansari.test |
| 0.2500 | 0.1092 | 0.0204 | 0.0204 | 0.1884 | 0.1808 | 0.0658 | 0.2382 | 0.9856 | 0.9276 |
| 0.2632 | 0.1080 | 0.0190 | 0.0190 | 0.1882 | 0.1816 | 0.0704 | 0.2442 | 0.9794 | 0.9152 |
| 0.2778 | 0.1080 | 0.0198 | 0.0198 | 0.1830 | 0.1750 | 0.0680 | 0.2386 | 0.9710 | 0.8948 |
| 0.2941 | 0.1096 | 0.0232 | 0.0232 | 0.1830 | 0.1754 | 0.0666 | 0.2336 | 0.9612 | 0.8740 |
| 0.3125 | 0.1034 | 0.0200 | 0.0200 | 0.1776 | 0.1708 | 0.0690 | 0.2310 | 0.9418 | 0.8546 |
| 0.3333 | 0.0996 | 0.0214 | 0.0214 | 0.1714 | 0.1652 | 0.0630 | 0.2110 | 0.9298 | 0.8334 |
| 0.3571 | 0.0934 | 0.0168 | 0.0168 | 0.1626 | 0.1554 | 0.0636 | 0.2070 | 0.9000 | 0.7920 |
| 0.3846 | 0.0962 | 0.0192 | 0.0192 | 0.1632 | 0.1552 | 0.0694 | 0.2090 | 0.8612 | 0.7378 |
| 0.4167 | 0.0828 | 0.0152 | 0.0152 | 0.1528 | 0.1452 | 0.0606 | 0.1848 | 0.8150 | 0.6810 |
| 0.4545 | 0.0838 | 0.0116 | 0.0116 | 0.1396 | 0.1324 | 0.0628 | 0.1640 | 0.7424 | 0.6064 |
| 0.5000 | 0.0832 | 0.0134 | 0.0134 | 0.1316 | 0.1244 | 0.0688 | 0.1614 | 0.6600 | 0.5224 |
| 0.5556 | 0.0826 | 0.0150 | 0.0150 | 0.1246 | 0.1188 | 0.0720 | 0.1438 | 0.5488 | 0.4160 |
| 0.6250 | 0.0736 | 0.0084 | 0.0084 | 0.1018 | 0.0960 | 0.0608 | 0.1150 | 0.4336 | 0.3120 |
| 0.7143 | 0.0758 | 0.0100 | 0.0100 | 0.0834 | 0.0796 | 0.0602 | 0.0912 | 0.3024 | 0.1880 |
| 0.8333 | 0.0724 | 0.0110 | 0.0110 | 0.0678 | 0.0644 | 0.0660 | 0.0716 | 0.2006 | 0.0890 |
| 1.0000 | 0.0698 | 0.0106 | 0.0106 | 0.0534 | 0.0490 | 0.0568 | 0.0510 | 0.1430 | 0.0488 |
| 1.2000 | 0.0752 | 0.0082 | 0.0082 | 0.0450 | 0.0408 | 0.0568 | 0.0348 | 0.1892 | 0.0772 |
| 1.4000 | 0.0738 | 0.0096 | 0.0096 | 0.0360 | 0.0322 | 0.0486 | 0.0198 | 0.2798 | 0.1628 |
| 1.6000 | 0.0770 | 0.0110 | 0.0110 | 0.0366 | 0.0344 | 0.0448 | 0.0186 | 0.3890 | 0.2596 |
| 1.8000 | 0.0926 | 0.0146 | 0.0146 | 0.0420 | 0.0388 | 0.0472 | 0.0176 | 0.5166 | 0.3820 |
| 2.0000 | 0.0990 | 0.0210 | 0.0210 | 0.0416 | 0.0370 | 0.0500 | 0.0148 | 0.6292 | 0.4882 |
| 2.2000 | 0.1172 | 0.0240 | 0.0240 | 0.0444 | 0.0418 | 0.0474 | 0.0094 | 0.7286 | 0.5924 |
| 2.4000 | 0.1350 | 0.0344 | 0.0344 | 0.0428 | 0.0388 | 0.0468 | 0.0088 | 0.7970 | 0.6710 |
| 2.6000 | 0.1558 | 0.0348 | 0.0348 | 0.0442 | 0.0420 | 0.0492 | 0.0096 | 0.8512 | 0.7264 |
| 2.8000 | 0.1624 | 0.0440 | 0.0440 | 0.0472 | 0.0444 | 0.0446 | 0.0076 | 0.8908 | 0.7860 |
| 3.0000 | 0.1736 | 0.0476 | 0.0476 | 0.0476 | 0.0420 | 0.0462 | 0.0064 | 0.9140 | 0.8178 |
| 3.2000 | 0.1864 | 0.0550 | 0.0550 | 0.0450 | 0.0414 | 0.0466 | 0.0080 | 0.9426 | 0.8486 |
| 3.4000 | 0.1972 | 0.0646 | 0.0646 | 0.0496 | 0.0448 | 0.0522 | 0.0070 | 0.9588 | 0.8732 |
| 3.6000 | 0.1954 | 0.0638 | 0.0638 | 0.0494 | 0.0450 | 0.0474 | 0.0058 | 0.9714 | 0.8912 |
| 3.8000 | 0.2176 | 0.0774 | 0.0774 | 0.0554 | 0.0490 | 0.0492 | 0.0064 | 0.9788 | 0.9080 |
| 4.0000 | 0.2306 | 0.0860 | 0.0860 | 0.0544 | 0.0500 | 0.0548 | 0.0076 | 0.9814 | 0.9184 |
3.3. 一様な分布の場合
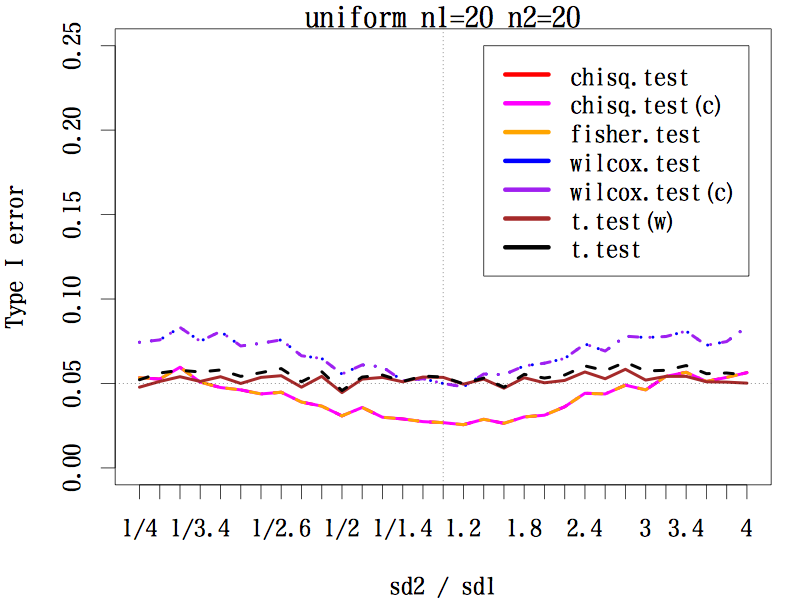
3.3.1. サンプルサイズが等しい場合(n1=20, n2=20)
どの検定手法でも第一種の過誤はほぼ 0.05 をキープしているが,標準偏差の比が 1/3 〜 3 のときの中央値検定は 0.05 よりかなり小さい。
 |
| 標準偏差の比 | chisq.test | chisq.test(c) | fisher.test | wilcox.test | wilcox.test(c) | t.test(w) | t.test | var.test | ansari.test |
| 0.2500 | 0.0534 | 0.0534 | 0.0534 | 0.0744 | 0.0744 | 0.0478 | 0.0522 | 1.0000 | 0.9946 |
| 0.2632 | 0.0526 | 0.0526 | 0.0526 | 0.0758 | 0.0758 | 0.0512 | 0.0562 | 1.0000 | 0.9918 |
| 0.2778 | 0.0596 | 0.0596 | 0.0596 | 0.0832 | 0.0832 | 0.0540 | 0.0578 | 0.9998 | 0.9840 |
| 0.2941 | 0.0508 | 0.0508 | 0.0508 | 0.0750 | 0.0750 | 0.0512 | 0.0568 | 1.0000 | 0.9812 |
| 0.3125 | 0.0476 | 0.0476 | 0.0476 | 0.0808 | 0.0808 | 0.0540 | 0.0580 | 0.9998 | 0.9734 |
| 0.3333 | 0.0462 | 0.0462 | 0.0462 | 0.0722 | 0.0722 | 0.0500 | 0.0542 | 1.0000 | 0.9586 |
| 0.3571 | 0.0438 | 0.0438 | 0.0438 | 0.0738 | 0.0738 | 0.0536 | 0.0564 | 0.9990 | 0.9554 |
| 0.3846 | 0.0448 | 0.0448 | 0.0448 | 0.0758 | 0.0758 | 0.0546 | 0.0588 | 0.9982 | 0.9314 |
| 0.4167 | 0.0390 | 0.0390 | 0.0390 | 0.0664 | 0.0664 | 0.0478 | 0.0510 | 0.9964 | 0.9000 |
| 0.4545 | 0.0366 | 0.0366 | 0.0366 | 0.0648 | 0.0648 | 0.0542 | 0.0570 | 0.9798 | 0.8532 |
| 0.5000 | 0.0308 | 0.0308 | 0.0308 | 0.0556 | 0.0556 | 0.0446 | 0.0458 | 0.9368 | 0.7786 |
| 0.5556 | 0.0358 | 0.0358 | 0.0358 | 0.0610 | 0.0610 | 0.0526 | 0.0538 | 0.7876 | 0.6618 |
| 0.6250 | 0.0300 | 0.0300 | 0.0300 | 0.0598 | 0.0598 | 0.0536 | 0.0550 | 0.5120 | 0.5142 |
| 0.7143 | 0.0290 | 0.0290 | 0.0290 | 0.0516 | 0.0516 | 0.0510 | 0.0512 | 0.2074 | 0.3212 |
| 0.8333 | 0.0274 | 0.0274 | 0.0274 | 0.0528 | 0.0528 | 0.0538 | 0.0544 | 0.0372 | 0.1306 |
| 1.0000 | 0.0268 | 0.0268 | 0.0268 | 0.0500 | 0.0500 | 0.0536 | 0.0538 | 0.0046 | 0.0492 |
| 1.2000 | 0.0256 | 0.0256 | 0.0256 | 0.0480 | 0.0480 | 0.0496 | 0.0498 | 0.0350 | 0.1278 |
| 1.4000 | 0.0288 | 0.0288 | 0.0288 | 0.0556 | 0.0556 | 0.0526 | 0.0532 | 0.2058 | 0.3178 |
| 1.6000 | 0.0264 | 0.0264 | 0.0264 | 0.0552 | 0.0552 | 0.0472 | 0.0478 | 0.5154 | 0.5040 |
| 1.8000 | 0.0302 | 0.0302 | 0.0302 | 0.0604 | 0.0604 | 0.0534 | 0.0554 | 0.7924 | 0.6554 |
| 2.0000 | 0.0312 | 0.0312 | 0.0312 | 0.0620 | 0.0620 | 0.0504 | 0.0532 | 0.9346 | 0.7790 |
| 2.2000 | 0.0362 | 0.0362 | 0.0362 | 0.0648 | 0.0648 | 0.0518 | 0.0550 | 0.9776 | 0.8462 |
| 2.4000 | 0.0442 | 0.0442 | 0.0442 | 0.0734 | 0.0734 | 0.0568 | 0.0604 | 0.9930 | 0.8980 |
| 2.6000 | 0.0438 | 0.0438 | 0.0438 | 0.0692 | 0.0692 | 0.0528 | 0.0576 | 0.9978 | 0.9264 |
| 2.8000 | 0.0490 | 0.0490 | 0.0490 | 0.0780 | 0.0780 | 0.0584 | 0.0626 | 0.9996 | 0.9494 |
| 3.0000 | 0.0462 | 0.0462 | 0.0462 | 0.0772 | 0.0772 | 0.0520 | 0.0574 | 1.0000 | 0.9700 |
| 3.2000 | 0.0542 | 0.0542 | 0.0542 | 0.0778 | 0.0778 | 0.0542 | 0.0578 | 0.9998 | 0.9738 |
| 3.4000 | 0.0566 | 0.0566 | 0.0566 | 0.0810 | 0.0810 | 0.0542 | 0.0606 | 1.0000 | 0.9844 |
| 3.6000 | 0.0512 | 0.0512 | 0.0512 | 0.0726 | 0.0726 | 0.0510 | 0.0558 | 1.0000 | 0.9868 |
| 3.8000 | 0.0536 | 0.0536 | 0.0536 | 0.0748 | 0.0748 | 0.0508 | 0.0562 | 1.0000 | 0.9874 |
| 4.0000 | 0.0564 | 0.0564 | 0.0564 | 0.0836 | 0.0836 | 0.0502 | 0.0550 | 1.0000 | 0.9918 |
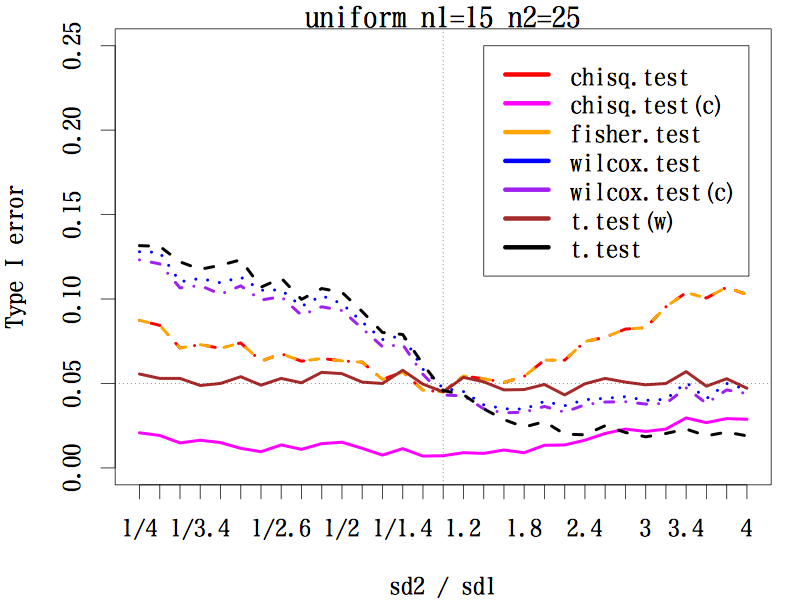
3.3.2. サンプルサイズが約 1:2 の場合(n1=15, n2=25)
ウェルチの方法による t 検定は,標準偏差の比がどのようであっても,第一種の過誤はほぼ 0.05 をキープしている。
連続性の補正をする中央値検定とフィッシャーの正確検定は同じ動きをしたが,標準偏差の比が 1 から離れると第一種の過誤はかなり大きくなる。一方,連続性の補正をする中央値検定では第一種の過誤は相当小さい。
 |
| 標準偏差の比 | chisq.test | chisq.test(c) | fisher.test | wilcox.test | wilcox.test(c) | t.test(w) | t.test | var.test | ansari.test |
| 0.2500 | 0.0874 | 0.0208 | 0.0874 | 0.1280 | 0.1232 | 0.0556 | 0.1316 | 1.0000 | 0.9820 |
| 0.2632 | 0.0844 | 0.0192 | 0.0844 | 0.1276 | 0.1208 | 0.0530 | 0.1312 | 1.0000 | 0.9762 |
| 0.2778 | 0.0710 | 0.0148 | 0.0710 | 0.1102 | 0.1066 | 0.0530 | 0.1220 | 0.9998 | 0.9742 |
| 0.2941 | 0.0730 | 0.0164 | 0.0730 | 0.1122 | 0.1080 | 0.0488 | 0.1176 | 1.0000 | 0.9706 |
| 0.3125 | 0.0708 | 0.0150 | 0.0708 | 0.1096 | 0.1028 | 0.0500 | 0.1200 | 1.0000 | 0.9568 |
| 0.3333 | 0.0740 | 0.0116 | 0.0740 | 0.1130 | 0.1078 | 0.0540 | 0.1232 | 0.9988 | 0.9460 |
| 0.3571 | 0.0632 | 0.0096 | 0.0632 | 0.1052 | 0.0994 | 0.0490 | 0.1070 | 0.9980 | 0.9336 |
| 0.3846 | 0.0676 | 0.0136 | 0.0676 | 0.1054 | 0.1014 | 0.0530 | 0.1124 | 0.9952 | 0.9102 |
| 0.4167 | 0.0632 | 0.0110 | 0.0632 | 0.0956 | 0.0904 | 0.0504 | 0.0998 | 0.9876 | 0.8698 |
| 0.4545 | 0.0648 | 0.0144 | 0.0648 | 0.1020 | 0.0954 | 0.0566 | 0.1062 | 0.9678 | 0.8144 |
| 0.5000 | 0.0634 | 0.0152 | 0.0634 | 0.0972 | 0.0932 | 0.0558 | 0.1040 | 0.9242 | 0.7406 |
| 0.5556 | 0.0626 | 0.0116 | 0.0626 | 0.0864 | 0.0826 | 0.0508 | 0.0926 | 0.7874 | 0.6262 |
| 0.6250 | 0.0524 | 0.0076 | 0.0524 | 0.0760 | 0.0718 | 0.0500 | 0.0802 | 0.5352 | 0.4896 |
| 0.7143 | 0.0568 | 0.0114 | 0.0568 | 0.0784 | 0.0730 | 0.0578 | 0.0790 | 0.2186 | 0.3092 |
| 0.8333 | 0.0460 | 0.0070 | 0.0460 | 0.0584 | 0.0554 | 0.0496 | 0.0614 | 0.0356 | 0.1396 |
| 1.0000 | 0.0450 | 0.0072 | 0.0450 | 0.0472 | 0.0432 | 0.0450 | 0.0458 | 0.0042 | 0.0502 |
| 1.2000 | 0.0544 | 0.0090 | 0.0544 | 0.0452 | 0.0426 | 0.0536 | 0.0434 | 0.0278 | 0.1274 |
| 1.4000 | 0.0528 | 0.0086 | 0.0528 | 0.0374 | 0.0350 | 0.0510 | 0.0350 | 0.1482 | 0.3052 |
| 1.6000 | 0.0506 | 0.0106 | 0.0506 | 0.0350 | 0.0326 | 0.0462 | 0.0286 | 0.3970 | 0.4850 |
| 1.8000 | 0.0542 | 0.0090 | 0.0542 | 0.0348 | 0.0330 | 0.0464 | 0.0242 | 0.6878 | 0.6428 |
| 2.0000 | 0.0638 | 0.0134 | 0.0638 | 0.0394 | 0.0364 | 0.0494 | 0.0274 | 0.8816 | 0.7698 |
| 2.2000 | 0.0638 | 0.0136 | 0.0638 | 0.0368 | 0.0330 | 0.0432 | 0.0200 | 0.9682 | 0.8522 |
| 2.4000 | 0.0748 | 0.0164 | 0.0748 | 0.0404 | 0.0374 | 0.0498 | 0.0196 | 0.9906 | 0.8916 |
| 2.6000 | 0.0774 | 0.0204 | 0.0774 | 0.0412 | 0.0390 | 0.0530 | 0.0250 | 0.9978 | 0.9312 |
| 2.8000 | 0.0822 | 0.0230 | 0.0822 | 0.0422 | 0.0392 | 0.0508 | 0.0210 | 0.9996 | 0.9512 |
| 3.0000 | 0.0830 | 0.0216 | 0.0830 | 0.0400 | 0.0378 | 0.0492 | 0.0184 | 0.9998 | 0.9636 |
| 3.2000 | 0.0954 | 0.0230 | 0.0954 | 0.0406 | 0.0382 | 0.0500 | 0.0204 | 1.0000 | 0.9754 |
| 3.4000 | 0.1038 | 0.0296 | 0.1038 | 0.0506 | 0.0474 | 0.0570 | 0.0230 | 1.0000 | 0.9820 |
| 3.6000 | 0.1006 | 0.0268 | 0.1006 | 0.0410 | 0.0382 | 0.0484 | 0.0190 | 1.0000 | 0.9880 |
| 3.8000 | 0.1070 | 0.0292 | 0.1070 | 0.0500 | 0.0462 | 0.0528 | 0.0212 | 1.0000 | 0.9880 |
| 4.0000 | 0.1026 | 0.0288 | 0.1026 | 0.0464 | 0.0440 | 0.0472 | 0.0190 | 1.0000 | 0.9910 |
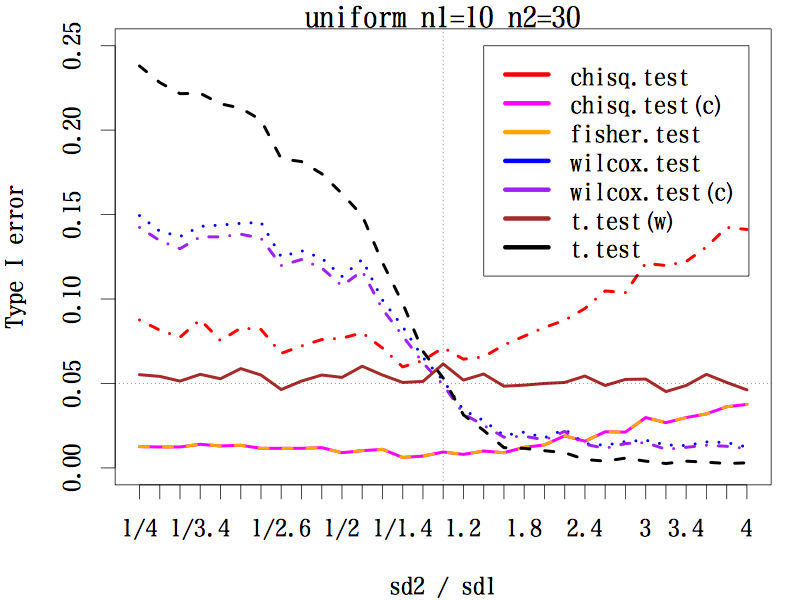
3.3.3. サンプルサイズが 1:3 の場合(n1=10, n2=30)
等分散を仮定する t 検定は破滅的である。マン・ホイットニーの U 検定も程度は弱いが同じ傾向である。
連続性の補正をする中央値検定とフィッシャーの正確検定は同じ動きをしたが,は全般的に第一種の過誤は 0.05 よりかなり低い。一方,連続性の補正をしない中央値検定の第一種の過誤はかなり大きい。
ウェルチの方法による t 検定は,標準偏差の比がどのようであっても,第一種の過誤はほぼ 0.05 をキープしている。
 |
| 標準偏差の比 | chisq.test | chisq.test(c) | fisher.test | wilcox.test | wilcox.test(c) | t.test(w) | t.test | var.test | ansari.test |
| 0.2500 | 0.0876 | 0.0126 | 0.0126 | 0.1494 | 0.1424 | 0.0552 | 0.2380 | 0.9994 | 0.9482 |
| 0.2632 | 0.0816 | 0.0124 | 0.0124 | 0.1402 | 0.1346 | 0.0542 | 0.2282 | 0.9990 | 0.9404 |
| 0.2778 | 0.0774 | 0.0124 | 0.0124 | 0.1370 | 0.1298 | 0.0514 | 0.2216 | 0.9992 | 0.9314 |
| 0.2941 | 0.0878 | 0.0140 | 0.0140 | 0.1430 | 0.1368 | 0.0554 | 0.2218 | 0.9974 | 0.9196 |
| 0.3125 | 0.0754 | 0.0130 | 0.0130 | 0.1438 | 0.1368 | 0.0528 | 0.2156 | 0.9962 | 0.9064 |
| 0.3333 | 0.0828 | 0.0134 | 0.0134 | 0.1448 | 0.1384 | 0.0588 | 0.2130 | 0.9946 | 0.8820 |
| 0.3571 | 0.0820 | 0.0116 | 0.0116 | 0.1454 | 0.1360 | 0.0550 | 0.2060 | 0.9884 | 0.8574 |
| 0.3846 | 0.0678 | 0.0116 | 0.0116 | 0.1250 | 0.1198 | 0.0464 | 0.1830 | 0.9798 | 0.8146 |
| 0.4167 | 0.0722 | 0.0116 | 0.0116 | 0.1286 | 0.1234 | 0.0514 | 0.1814 | 0.9624 | 0.7664 |
| 0.4545 | 0.0760 | 0.0120 | 0.0120 | 0.1242 | 0.1184 | 0.0550 | 0.1742 | 0.9214 | 0.7074 |
| 0.5000 | 0.0768 | 0.0090 | 0.0090 | 0.1134 | 0.1078 | 0.0536 | 0.1624 | 0.8478 | 0.6444 |
| 0.5556 | 0.0800 | 0.0102 | 0.0102 | 0.1234 | 0.1166 | 0.0602 | 0.1494 | 0.6934 | 0.5520 |
| 0.6250 | 0.0710 | 0.0110 | 0.0110 | 0.0994 | 0.0940 | 0.0550 | 0.1216 | 0.4682 | 0.4160 |
| 0.7143 | 0.0598 | 0.0062 | 0.0062 | 0.0836 | 0.0782 | 0.0506 | 0.0974 | 0.1984 | 0.2746 |
| 0.8333 | 0.0636 | 0.0070 | 0.0070 | 0.0654 | 0.0622 | 0.0512 | 0.0690 | 0.0354 | 0.1326 |
| 1.0000 | 0.0712 | 0.0094 | 0.0094 | 0.0518 | 0.0492 | 0.0616 | 0.0532 | 0.0088 | 0.0502 |
| 1.2000 | 0.0644 | 0.0080 | 0.0080 | 0.0342 | 0.0320 | 0.0520 | 0.0314 | 0.0254 | 0.0922 |
| 1.4000 | 0.0658 | 0.0100 | 0.0100 | 0.0280 | 0.0252 | 0.0556 | 0.0222 | 0.0838 | 0.2302 |
| 1.6000 | 0.0728 | 0.0090 | 0.0090 | 0.0192 | 0.0182 | 0.0484 | 0.0120 | 0.2110 | 0.3728 |
| 1.8000 | 0.0780 | 0.0122 | 0.0122 | 0.0212 | 0.0188 | 0.0490 | 0.0116 | 0.4108 | 0.5374 |
| 2.0000 | 0.0832 | 0.0136 | 0.0136 | 0.0178 | 0.0166 | 0.0500 | 0.0102 | 0.6294 | 0.6586 |
| 2.2000 | 0.0874 | 0.0190 | 0.0190 | 0.0228 | 0.0216 | 0.0506 | 0.0090 | 0.8194 | 0.7502 |
| 2.4000 | 0.0944 | 0.0158 | 0.0158 | 0.0144 | 0.0140 | 0.0544 | 0.0050 | 0.9330 | 0.8264 |
| 2.6000 | 0.1048 | 0.0214 | 0.0214 | 0.0134 | 0.0116 | 0.0488 | 0.0040 | 0.9738 | 0.8760 |
| 2.8000 | 0.1038 | 0.0212 | 0.0212 | 0.0156 | 0.0144 | 0.0524 | 0.0058 | 0.9942 | 0.9122 |
| 3.0000 | 0.1212 | 0.0298 | 0.0298 | 0.0164 | 0.0150 | 0.0526 | 0.0040 | 0.9980 | 0.9312 |
| 3.2000 | 0.1198 | 0.0268 | 0.0268 | 0.0136 | 0.0110 | 0.0452 | 0.0026 | 0.9992 | 0.9504 |
| 3.4000 | 0.1222 | 0.0298 | 0.0298 | 0.0132 | 0.0122 | 0.0488 | 0.0040 | 1.0000 | 0.9614 |
| 3.6000 | 0.1308 | 0.0320 | 0.0320 | 0.0154 | 0.0134 | 0.0554 | 0.0034 | 1.0000 | 0.9634 |
| 3.8000 | 0.1424 | 0.0362 | 0.0362 | 0.0150 | 0.0128 | 0.0506 | 0.0026 | 1.0000 | 0.9714 |
| 4.0000 | 0.1412 | 0.0376 | 0.0376 | 0.0124 | 0.0114 | 0.0462 | 0.0030 | 1.0000 | 0.9788 |
3.4. その他のサンプルサイズの場合
条件は同じで,サンプルサイズとして (n1, n2) = (5, 5), (5, 10), (5, 15), (50, 50), (50, 100), (50, 150) の場合についてもシミュレーションを行ったが,結論は同じようなものであった。すなわち,どのような場合にもウェルチの検定の第一種の過誤はほぼ 0.05 で安定していた。
4. 結論
メディアン検定は,標準偏差の比の違いに影響を受けないということは事実であるが,それをまるっきり打ち消してしまう欠点がある。すなわち,第一種の過誤が小さすぎる。これは第二種の過誤が大きくなり,検出力が低くなることを意味している。
等分散を仮定しない t 検定(ウェルチの方法)は,標準偏差の比 1/4 〜 4 の全てにおいて,また,サンプルサイズのアンバランスな全ての状況において,さらに,データの分布型の全てにおいて,第一種の過誤が 0.05 にキープされていることが示された。
等分散を仮定する t 検定は,当然のことながら,標準偏差の比が 1 から外れると第一種の過誤は 0.05 とはかけ離れたものになる。マン・ホイットニーの U 検定検定は等分散を仮定する t 検定ほどではないが,推薦できるようなものではない。
今回のシミュレーションは間隔尺度以上のデータを仮定したものである。順序尺度のデータの場合には今回のシミュレーションは回答を与えないのではないかといわれるかもしれない。しかし,マン・ホイットニーの U 検定が純粋な順序尺度で測定されたデータに適用されることのほうがむしろまれなのではないだろうか。間隔尺度データ(と見なせるデータ)を検定の対象にするとき,例数が少ないことや等分散でないことを理由にマン・ホイットニーの U 検定を採用することの方が多いであろう。そして,粕谷は等分散でないデータにマン・ホイットニーの U 検定やクラスカル・ウォリス検定は適用できないといっている。そして,「順序尺度の場合には中央値検定,間隔尺度・比尺度の場合には等分散を仮定しない t 検定,あるいは等分散検定後に普通の t 検定」を提唱しているのである。この後半が抜け落ちたまま,【不等分散の場合には中央値検定】と短絡的に受け取っている読者がおおいようだ。なお,事前検定を行うことが不適切であることはだんだん理解されてきているので,この観点から言えば「等分散検定後に普通の t 検定」というのは好ましくない。分散が等しかろうと等しくなかろうと,最初からズバリ「等分散を仮定しない t 検定」を行うのが正しいやり方である。
5. まとめ
二群の代表値を検定するときで,二群の分散が等しくないときには,等分散を仮定しない t 検定を採用するのが望ましい。
サンプルサイズがほぼ等しい場合には,等分散を仮定する t 検定,仮定しない t 検定,連続性の補正をするしないに関わらずマン・ホイットニーの U 検定は,標準偏差の比の違いに関係なく第一種の過誤はほぼ 0.05 をキープしている。そのような場合であっても,中央値検定は 0.05 よりかなり低いレベルにとどまっている。そのようなことを考えると,実験デザインをくむ段階では二群のサンプルサイズはそろえるべきであろう。
追記
3 群の場合で,サンプルサイズが(20, 20, 20), (20, 30, 40), (20, 40, 60) の 3 通り,分布は本文中のように 3 種類,標準偏差の比を,第二群は 1 〜 4 まで 0.2 刻み,第三群は 1 〜 1/4 まで分母を 0.2 刻みでシミュレーションした。検定は,中央値検定,クラスカル・ウォリス検定,一元配置分散分析,等分散性を仮定しない一元配置分散分析である。
その結果,あらゆる条件の下で等分散性を仮定しない一元配置分散分析の第一種の過誤はほぼ 0.05 をキープしている(参考図)。
結論としては,母分散の異なる(可能性のある)3 群以上の平均値の差には,予備検定なしで等分散性を仮定しない一元配置分散分析を行うことが推奨される。
参考文献
1) Kasuya, E. (2001): Mann-Whitney U test when variances are unequal. Animal Behaviour 61: 1247-1249.
pdf ファイル
2) Markus Neuhäuser (2002): Two-sample tests when variances are unequal. Animal Behaviour 63: 823-825.
pdf ファイル
ご意見・ご希望,間違いの指摘等がありましたら,
下記宛へ E-mail いただくと,たいへんうれしく思います。
 E-mail to Shigenobu AOKI
E-mail to Shigenobu AOKI












