目的

Cutler - Ederer 法による生命表を作成する

使用法

ce.surv(time, event, width)	# 原データから作成
ce.surv2(ni, d, u, interval)	# 二次データから作成

引数

time      生存期間ベクトル
event     死亡なら 1，生存なら 0 の値をとるベクトル
width     生存率を計算する区間幅
ni        初期例数
d         死亡数ベクトル
u         打ち切り数ベクトル
interval  区間数値ベクトル

ソース

インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/ce_surv.R", encoding="euc-jp")

# Cutler - Ederer 法による生命表
# 原データから作成
ce.surv<- function(  time,                                   # 生存期間ベクトル
                        event,                                  # 死亡なら 1，生存なら 0 の値をとるベクトル
                        width)                                  # 生存率を計算する区間幅
{
        OK <- complete.cases(time, event)                    # 欠損値を持つケースを除く
        time <- time[OK]
        event <- event[OK]
        ni <- length(time)                                   # 初期例数
        time <- floor(time/width)                            # 生存期間を区間に分ける
        tbl <- table(factor(time, level=0:max(time)), event) # 集計して二次データを作り，下請け関数を呼ぶ
        ce.surv2(ni, tbl[,2], tbl[,1], seq(0, width*(nrow(tbl)-1), width))
        
}
# 二次データから作成
ce.surv2 <- function(        ni,                                     # 初期例数
                        d,                                      # 死亡数ベクトル
                        u,                                      # 打ち切り数ベクトル
                        interval)                               # 区間数値ベクトル
{
        k <- length(d)                       
        stopifnot(length(u) == k && length(interval) == k)        # 長さが同じであること
        n <- rep(ni, k)-cumsum(d+u)                          # 各区間の開始時における例数
        n <- c(ni, n[-k])
        np <- n-u/2                                          # 区間中央の例数
        q <- d/np                                            # 死亡率
        p <- 1-q                                             # 生存率
        P <- cumprod(p)                                              # 累積生存率
        SE <- P*sqrt(cumsum(q/(n-u/2-d)))                    # 累積生存率の標準誤差
        result <- data.frame(interval, n, d, u, np, q, p, P, SE)
        interval <- c(interval, max(interval)+interval[2]-interval[1])
        P <- c(1, P)
        plot(interval, P, type="o", xlim=c(0, max(interval)), ylim=c(0, 1))
        return(result)
}


使用例

# 富永祐民「治療効果判定のための実用統計学 − 生命表法の解説 −」蟹書房(第3回改訂版）74 ページ，表 4.1 のデータ
# 解析結果は 78-79 ページ

# 1 は A 群，2 は B 群を表す
> group <- c(1, 1, 2, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 1, 2, 2, 2, 1, 1, 2, 1, 2, 1, 2, 1, 2, 2, 1, 1, 1)

# 1 は死亡，0 は 生存（打ち切り）を表す
> event <- c(1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0)

# 生存期間
> time <- c(2, 20, 5, 1, 3, 17, 2, 3, 15, 14, 12, 13, 11, 11, 10, 8, 8, 3, 7, 3, 6, 2, 5, 4, 2, 3, 1, 3, 2, 1)
 
# A 群についての解析

> a.group <- group == 1
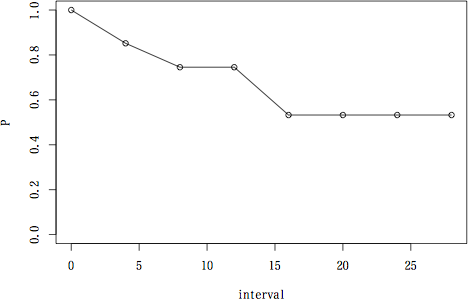
> ce.surv(time[a.group], event[a.group], 4)
  interval  n d u   np         q         p         P         SE
0        0 16 2 5 13.5 0.1481481 0.8518519 0.8518519 0.09668593
1        4  9 1 2  8.0 0.1250000 0.8750000 0.7453704 0.13068362
2        8  6 0 2  5.0 0.0000000 1.0000000 0.7453704 0.13068362
3       12  4 1 1  3.5 0.2857143 0.7142857 0.5324074 0.20275239
4       16  2 0 1  1.5 0.0000000 1.0000000 0.5324074 0.20275239
5       20  1 0 0  1.0 0.0000000 1.0000000 0.5324074 0.20275239
6       24  1 0 1  0.5 0.0000000 1.0000000 0.5324074 0.20275239



# B 群についての解析

> b.group <- group == 2
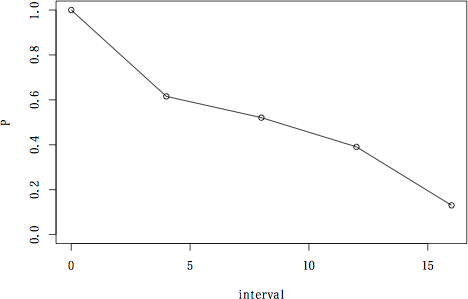
> ce.surv(time[b.group], event[b.group], 4)
  interval  n d u   np         q         p         P        SE
0        0 14 5 2 13.0 0.3846154 0.6153846 0.6153846 0.1349320
1        4  7 1 1  6.5 0.1538462 0.8461538 0.5207101 0.1435961
2        8  5 1 2  4.0 0.2500000 0.7500000 0.3905325 0.1559112
3       12  2 1 1  1.5 0.6666667 0.3333333 0.1301775 0.1590466





二次データから計算する場合

> ni <- 37
> interval <- seq(0, 120, 10)
> d <- c(3, 2, 3, 4, 1, 2, 3, 1, 0, 1, 0, 0, 0)
> u <- c(8, 3, 1, 4, 0, 0, 0, 0, 0, 0, 0, 0, 1)

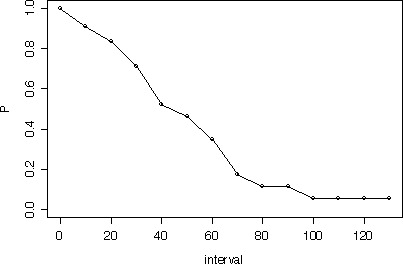
> ce.surv2(ni, d, u, interval)

      interval  n d u   np          q         p          P         SE
 [1,]        0 37 3 8 33.0 0.09090909 0.9090909 0.90909091 0.05004381
 [2,]       10 26 2 3 24.5 0.08163265 0.9183673 0.83487941 0.06812545
 [3,]       20 21 3 1 20.5 0.14634146 0.8536585 0.71270193 0.08734827
 [4,]       30 17 4 4 15.0 0.26666667 0.7333333 0.52264808 0.10356244
 [5,]       40  9 1 0  9.0 0.11111111 0.8888889 0.46457607 0.10710681
 [6,]       50  8 2 0  8.0 0.25000000 0.7500000 0.34843206 0.10729149
 [7,]       60  6 3 0  6.0 0.50000000 0.5000000 0.17421603 0.08908649
 [8,]       70  3 1 0  3.0 0.33333333 0.6666667 0.11614402 0.07599690
 [9,]       80  2 0 0  2.0 0.00000000 1.0000000 0.11614402 0.07599690
[10,]       90  2 1 0  2.0 0.50000000 0.5000000 0.05807201 0.05594695
[11,]      100  1 0 0  1.0 0.00000000 1.0000000 0.05807201 0.05594695
[12,]      110  1 0 0  1.0 0.00000000 1.0000000 0.05807201 0.05594695
[13,]      120  1 0 1  0.5 0.00000000 1.0000000 0.05807201 0.05594695



 解説ページ