例題：

　「表 1 に示すようなデータに曲線をあてはめなさい。」

考え方：

1. 元のデータをプロットすると図 1 のようになる。

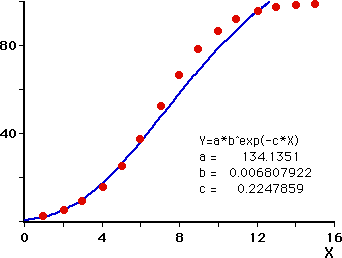
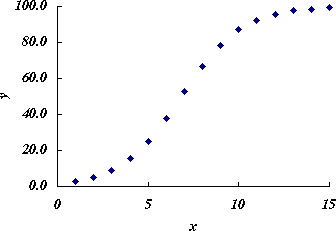
   図 1．元データのプロット

2. 独立変数は，１から始まる連続する整数とする。従属変数は全て正の値でなければならない（ 0 も不可 ）。

   注1： より妥当なあてはめを行う場合には，非線形最小二乗あてはめを行う。

   注2： データが飽和点に達していない部分のみ（ 指数的な増加部分だけ ）の場合には，あてはめに失敗する場合がある。このような場合には非線形最小二乗法によるあてはめを行う。

3. ゴンペルツ曲線を表す $(1)$ 式の両辺の対数をとると，$(2)$ 式のようになる。

   \[ y = a\ b^{\exp(-c\ x)} \tag{1} \] \[ \log y = \log a+\log b\ \exp(-c\ x) \tag{2} \]

4. ここで，Y = log y，A = log a，B = log b とおくと（ 3 ）式のようになる。

   \[ Y = A+B\ \exp(-c\ x) \tag{3} \]

5. $(3)$ 式は，未知のパラメータ $A$，$B$ については線形であるが，$c$ については非線形である。そこで，以下のような逐次的に近似する手法をとる。
   1. パラメータ $c$ の初期近似値を $c_{1}$ とする（ $c = c_{1} + \delta$ ）。 \[ \exp(-c\ x) ≒ \exp(-c_1\ x)-\delta\ x\ \exp(-c_1\ x) \]
   2. $(3)$ 式に代入して， \[ Y = A+B\ \left \{ \exp(-c_1\ x)-\delta\ x\ \exp(-c_1\ x) \right \} \]
   3. $X_{1} = \exp ( - c_{1} x )$ ，$X_{2} = x\ \exp ( - c_{1} x ) $，$C = B\ \delta$ とおくと， \[ Y = A+B\ X_1-C\ X_2 \tag{4} \]
   4. $(4)$ 式は，2 個の独立変数（ $X_{1}$，$X_{2}$ ）からなる重回帰式であるので，$A$，$B$，$C$ を求めることができる。

   5. $c$ の近似値 $c_{1}$ の改良値 $c_{2}$ は，$\delta = C / B$ であるから，$c_{2} = c_{1} + \delta$ と表される。

   6. パラメータ $c$ の修正量 $\delta$ が十分小さくなるまで（ 4 ）式の重回帰式を繰返して計算する。

   例題では，$c_{1} = 0.2$ とすると以下のようになる。

   c1 = 0.2
              x        y    Y=ln(y)      X1        X2
               1      2.9   1.06471  0.81873   0.81873
               2      5.2   1.64866  0.67032   1.34064
               3      9.1   2.20827  0.54881   1.64643
               4     15.5   2.74084  0.44933   1.79732
               5     25.0   3.21888  0.36788   1.83940
               6     37.8   3.63231  0.30119   1.80717
               7     52.6   3.96272  0.24660   1.72618
               8     66.9   4.20320  0.20190   1.61517
               9     78.6   4.36437  0.16530   1.48769
              10     87.0   4.46591  0.13534   1.35335
              11     92.4   4.52613  0.11080   1.21883
              12     95.7   4.56122  0.09072   1.08862
              13     97.6   4.58088  0.07427   0.96556
              14     98.6   4.59107  0.06081   0.85134
              15     99.2   4.59714  0.04979   0.74681
   
   $A = 4.8637835$
   B = -4.970501
   C = -0.135046
   
   a = exp( 4.86378350866624) = 129.513290946697
   b = exp(-4.97050111528571) = 0.00693966958875897
   c2 = 0.2 - 0.135045637341107 / -4.97050111528571 = 0.227169420991739
   
              x        y    Y=ln(y)      X1        X2
               1      2.9   1.06471  0.79679   0.79679
               2      5.2   1.64866  0.63487   1.26974
               3      9.1   2.20827  0.50585   1.51756
               4     15.5   2.74084  0.40306   1.61223
               5     25.0   3.21888  0.32115   1.60575
               6     37.8   3.63231  0.25589   1.53533
               7     52.6   3.96272  0.20389   1.42721
               8     66.9   4.20320  0.16245   1.29964
               9     78.6   4.36437  0.12944   1.16498
              10     87.0   4.46591  0.10314   1.03137
              11     92.4   4.52613  0.08218   0.90396
              12     95.7   4.56122  0.06548   0.78574
              13     97.6   4.58088  0.05217   0.67824
              14     98.6   4.59107  0.04157   0.58198
              15     99.2   4.59714  0.03312   0.49684
   
   $A = 4.900239$
   B = -4.988447
   C = 0.0135187
   
   a = exp( 4.90023902483658) = 134.321882114064
   b = exp(-4.98844737035507) = 0.0068162393759893
   c3 = 0.227169420991739 + 0.0135187429340499 / -4.98844737035507 = 0.224459410856243
   					：
   					：
   

図 2．あてはめ結果

R で計算してみる

演習問題：

応用問題：