母比率の検定の手順の，$F$ 分布による方法（二項検定と等価）において，
　　自由度が $\nu_{1}, \nu_{2})$ の $F$ 分布において，有意確率を $P = 2 \times \Pr\{F \geqq F_0\}$
として，評価しているところがある。この方法は，二項分布が左右対称（に近い）ことを想定している。
　そのような状況が想定できるのは，母比率が $0.5$ に近い場合，または，母比率が $0.5$ とかなり異なっていても標本サイズが大きい場合である（二項分布のページを参照のこと）。
　両側検定の有意確率は，分布がほぼ左右対称ならば，「観察された場合を含みそれより極端な場合の生起確率の和の 2 倍」として定義できる（普通の定義）。しかし，分布が左右対称でないならば，片方の生起確率を 2 倍するのでは不適切である。そのような場合には，複数の考え方があるが，Fisher の正確確率検定において採用された定義は，「観察された事象の生起確率より小さい生起確率の総和を両側確率とする」というものである（有意確率の決定法のページを参照のこと）。

　R，[Python] では，母比率の検定は，$F$ 分布を用いた正確な検定と等価な二項検定（二項分布を用いる検定）として行われる。そして，有意確率は後者の定義によって算出される。
　母比率の検定に示した例題をそこに示した手順で解くと，$P = 0.2397$ ということになる。しかし，R によれば，以下のように $P = 0.1198$ ということになる。

> binom.test(2, 20, p=0.03)

	Exact binomial test

data:  2 and 20 
number of successes = 2, number of trials = 20, p-value = 0.1198
alternative hypothesis: true probability of success is not equal to 0.03 
以下略

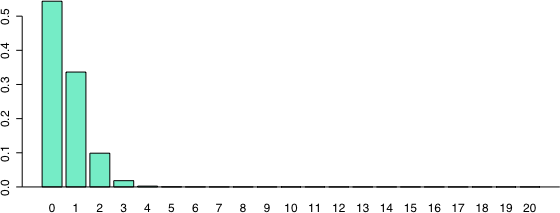
　$P$ 値が 2 倍も違うとは，驚くかもしれないが，二項分布のグラフを描いてみると一目瞭然である。
　つまり，$x=2$ のときの二項分布の確率密度より小さいのは，右側にしかない。よって，先の定義によれば，$x=2, 3, \dots, 20$ の確率密度の和 $0.119838$ が，求める有意確率なのである。

二項分布の確率密度

$x$	確率密度 $f(x)\%$	累積和
0	0.543794	1.000000
1	0.336368	0.456206
2	0.098830	0.119838
3	0.018340	0.021008
4	0.002411	0.002669
5	0.000239	0.000258
6	0.000018	0.000020
7	0.000001	0.000001
8	5.735E-08	5.979E-08
9	2.365E-09	2.448E-09
10	8.045E-11	8.277E-11
11	2.262E-12	2.315E-12
12	5.247E-14	5.348E-14
13	9.986E-16	1.014E-15
14	1.544E-17	1.564E-17
15	1.910E-19	1.929E-19
16	1.846E-21	1.860E-21
17	1.344E-23	1.351E-23
18	6.926E-26	6.949E-26
19	2.255E-28	2.258E-28
20	3.487E-31	3.487E-31

演習問題：

応用問題：