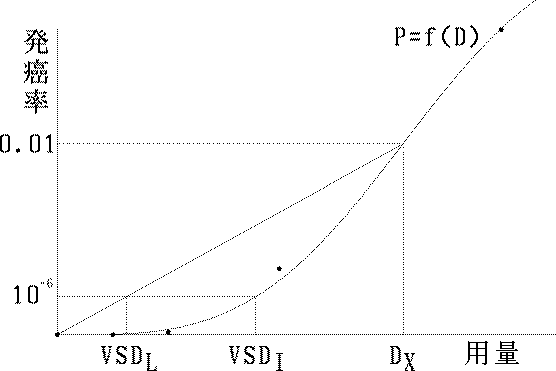
 図 4.直線外挿による VSD の求め方 |
VSDは,用量 - 反応関数 $P = f ( D )$ の逆関数 $D = f^{- 1} ( P )$ を用いて推定する。例えば,自然発癌率 $p \gt 0$ の Weibull model のとき,( 14 )式の逆関数は( 17 )式のように表せる。
\[ f^{-1}(P) = \sqrt[m]{\frac{-\alpha-\log(1-P)}{\beta}} \tag{17} \] 自然発癌率 $p$ より $P$ だけ大きい発癌率 ( 超過リスク ) が予想される用量は,( 18 )式により求められる。
\[ D = f^{-1}(P+p) = \sqrt[m]{\frac{-\alpha-\log(1-P-p)}{\beta}} \tag{18} \] VSD というのは,超過リスクが極めて小さい場合の対応する用量であり,$P$ としては,$10^{-6}$,$10^{-8}$ などが使われる。発癌試験が慢性投与・生涯曝露の形式で行われるとき,$10^{-6}$ とは,用量 $D$ を生涯摂取し続けた場合に,その個体が発癌する( 超過リスクの )確率である。これは,日本の人口を $1$ 億人,平均寿命を $70$ 歳としたとき,当該物質により毎年 $10^{-6}\times 10^8\ /\ 70 ≒ 1.4$ 人の発癌が新たに発生する( 自然発生率に加わる超過リスク )という意味を持つ。現在わが国で年間の癌死亡数が約 $20$ 万人であることを考えて,この数字が許容できるか否かを決定するのはリスクマネージメントの範疇に入る。なお,発癌試験が慢性投与・生涯曝露の形式でない場合には解釈の上で考慮が必要となる。
VSD を求める際に,上記のように直接 $P$ として低い確率を代入するのは,極低濃度の場合の用量 - 反応曲線が実験で用いられる範囲の濃度の場合と異なってくる可能性があるので,不適当なこともあろう。この場合には,発生率が観察できる程度の濃度をもとに直線外挿により VSD を求める( 図 4 参照 ) 。例えば,( 19 )式のように,超過発生率が $a \times 100\%$ となる用量を( 19 )式から求め,これに $10^{-6}\ /\ a$ を掛けることにより得られた値を VSD とすればよい。
リニアライズドマルチステージモデル( Linearized Multi - stage model )は,マルチステージモデルによる用量 - 反応曲線の上側信頼限界線(低用量領域では用量 - 反応曲線と同じく直線で近似できる。)を用いるものである。この意味では,上述した直線外挿とは若干異なる。また,後述する Gaylor - Kodel 法との類似点もある。
\[ \begin{align*} VSD & = f^{-1}(p+a)\times \frac{10^{-6}}{a} \\[5pt] & =\sqrt[m]{\frac{-\alpha-\log(1-P-p)}{\beta}} \times \frac{10^{-6}}{a} \end{align*} \tag{19} \]
 図 4.直線外挿による VSD の求め方 |