「統計学関連なんでもあり」の過去ログ--- 046

No.20342　非線形回帰のエラーについて　　【工藤】　2013/10/19(Sat) 00:56

今，Rを用いて，デジカメの普及曲線を調べようとしています。実行後，
step 因子0.000488281は0.000976562 の 'minFactor' 以下に縮小しました。
というエラーが出てしまいます。おおらく，初期値がおかしいからだと思いますが初期値を何度も変更しても同じエラーがずっと出てしまいます（初期値を上げても下げてもエラーが出てしまいます）。適切な初期値を調べる方法はあるのでしょうか。お忙しい所恐縮ですが，何卒よろしくお願いします。

因みに以下がプログラムコードになります。

Year <- 2002:2013
# デジカメの普及率
DR <- c(22.7, 32, 51.8, 46.2, 53.7, 58.9, 66, 69.2, 71.5, 73.3, 76.3, 77)
n <- length(DR)
X1 <- DR[1:(n - 1)]
X2 <- X1^2
Y <- DR[2:n] - X1
W <- DR[1:n]
period <- 1:n

## バスモデルのパラメータの推定
M2 <- nls(W ~ m * (1 - exp(-(p + q) * period))/(1 + q/p * exp(-(p + q) * period)), 
    start = list(p = 0.02, q = 0.1, m = max(W)), trace = TRUE)

para <- M2$m$getPars()

## 推定したパラメータによる普及率の予測
p.hat <- para[1]
q.hat <- para[2]
m.hat <- para[3]

W.hat <- m.hat * (1 - exp(-(p.hat + q.hat) * period))/(1 + q.hat/p.hat * exp(-(p.hat + 
    q.hat) * period))

plot(Year, W.hat, type = "l", lty = 1, ylab = "Diffusion rate(%)")
lines(Year, W, lty = 2)
legend(2002, 23, c("Predicted", "Observed"), lty = 1:2)

summary(M2)

No.20343　Re: 非線形回帰のエラーについて　　【青木繁伸】　2013/10/19(Sat) 08:12

シンプレックス法 http://aoki2.si.gunma-u.ac.jp/R/simplex.html であてはめると
> fun <- function(period, p) p[3]*(1-exp(-(p[1]+p[2])*period))/(1+p[2]/p[1]*exp(-(p[1]+p[2])*period))
> simplex(fun, c(0.02, 0.1, max(W)), period, W)
$converge
[1] TRUE

$parameters
[1]   0.2495198  -0.2494788 102.4757342

$residuals
[1] 117.194
のようになりますが，これを初期値として nls を適用すると
以下にエラー numericDeriv(form[[3L]], names(ind), env) :
モデルを評価する際，欠損値または無限大が生成されました
が出ますね。p と q がほとんど同じ値で符号が逆という微妙なモデルなので，数値偏微分がうまく働かないのかな。
分母の exp の前に q/p が付いていて，単純なロジスティック曲線じゃないのですね。
この辺りも，あてはめがうまくいかない原因になっているのかな？
nls(W ~ m*(1-exp(-(p+q)*period))/(1+q/p*exp(-(p+q)*period)),start=list(p= 0.7,q=-0.6,m=77),trace=TRUE,
 control=list(minFactor=1e-10, maxiter=100000))
でやってみると，「勾配が特異です」になりますからね。

適切な初期値を調べる方法は，パラメータに基づいて図を描き，値を変化させて図がどのようになるかを確認し値の変化量・方向を変えてまた図を描く。というようなことを繰り返す。エクセルなどを使うとやりやすいかも知れない。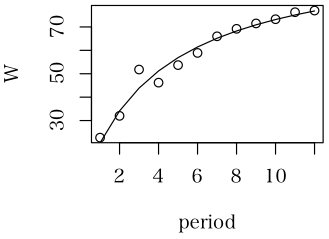

No.20344　Re: 非線形回帰のエラーについて　　【斜界人】　2013/10/19(Sat) 15:20

Bassモデルのことは知らなくて，Wikipediaで見ただけだから違っていたらご免なさい。
wikipediaによれば
x_t = m*(1-c0*exp(-(p+q)*priod))/(1+c0*q/p*exp(-(p+q)*period)
ここで，x_tは時点tでの購買者数，mは総需要となっています。DRは普及率なので，c0=1の標準モデルを考えると
DR_t = x_t / m = (1-exp(-(p+q)*priod))/(1+q/p*exp(-(p+q)*period)
となるのでは。mを定数100にするか，mを無くしてW=DR/100ならエラーにはならないです。
> M2<- nls(W ~ 100*(1-exp(-(p+q)*period))/(1+q/p*exp(-(p+q)*period)),start=list(p=0.02,q=0.1),trace=TRUE)
または，
> W <- DR/100
...
> M2<- nls(W ~ (1-exp(-(p+q)*period))/(1+q/p*exp(-(p+q)*period)),start=list(p=0.02,q=0.1),trace=TRUE)

No.20345　Re: 非線形回帰のエラーについて　　【青木繁伸】　2013/10/19(Sat) 19:49

オンラインヘルプを隅から隅まで読んでみると，
M2<- nls(W ~ m*(1-exp(-(p+q)*period))/(1+q/p*exp(-(p+q)*period)),start=list(p=1,q=2,m=max(W)),trace=TRUE,
algorithm="port", control=list(warnOnly = TRUE))
のようにすると，参考に出来る結果を得る事はできるとのこと。
Setting warnOnly = TRUE in the control argument (see nls.control) returns a non-converged object (since R version 2.5.0) which might be useful for further convergence analysis, but not for inference.

その他，algorithm も変える。algorithm="port",
> summary(M2)

Formula: W ~ m * (1 - exp(-(p + q) * period))/(1 + q/p * exp(-(p + q) * 
    period))

Parameters:
    Estimate Std. Error t value Pr(>|t|)
p     0.2495   156.8584   0.002    0.999
q    -0.2495   156.6818  -0.002    0.999
m   102.4964 64430.2652   0.002    0.999

Residual standard error: 3.609 on 9 degrees of freedom

Algorithm "port", convergence message: false convergence (8)

No.20346　Re: 非線形回帰のエラーについて　　【工藤】　2013/10/19(Sat) 23:12

斜界人さん

ご解答ありがとうございました。

斜界人さんのご指摘の通りに以下のプログラムで実行したとたところ，うまく図示する事ができました。
しかし，p=0.2,q=-0.2になりました。qの値がマイナスになっているのでこれはどのように解釈すればいいでしょうか（ただ***が付いているので有意水準は高いのですが・・・）。
# デジカメ
Year <- 2002:2013
DR <- c(22.7, 32, 51.8, 46.2, 53.7, 58.9, 66, 69.2, 71.5, 73.3, 76.3, 77)
n <- length(DR)
X1 <- DR[1:(n - 1)]
X2 <- X1^2
Y <- DR[2:n] - X1
W <- DR[1:n]
period <- 1:n

## バスモデルのパラメータの推定
M2 <- nls(W ~ 100 * (1 - exp(-(p + q) * period))/(1 + q/p * exp(-(p + q) * period)), 
    start = list(p = 0.02, q = 0.1), trace = TRUE)

para <- M2$m$getPars()

## 推定したパラメータによる普及率の予測
p.hat <- para[1]
q.hat <- para[2]
# m.hat <- para[3]

W.hat <- 100 * (1 - exp(-(p.hat + q.hat) * period))/(1 + q.hat/p.hat * exp(-(p.hat + 
    q.hat) * period))

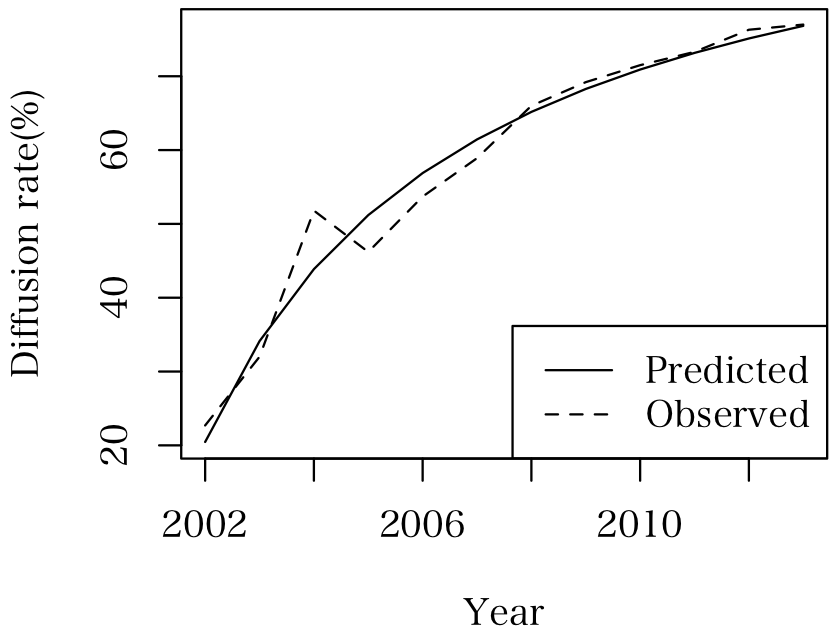
plot(Year, W.hat, type = "l", lty = 1, ylab = "Diffusion rate(%)")
lines(Year, W, lty = 2)
legend(2003, 23, c("Predicted", "Observed"), lty = 1:2)

summary(M2)

No.20347　Re: 非線形回帰のエラーについて　　【工藤】　2013/10/19(Sat) 23:26

青木繁伸さん

algorithm="port"とはどういった意味しょうか。お教え頂ければ幸いです。
また，qの値がマイナスになってしまいます。図はうまく描写する事が出来ましたが，これは誤りでしょうか。

No.20349　Re: 非線形回帰のエラーについて　　【青木繁伸】　2013/10/20(Sun) 08:53

> algorithm="port"とはどういった意味しょうか

オンラインヘルプを読みましょう。

algorithm
character string specifying the algorithm to use. The default algorithm is a Gauss-Newton algorithm. Other possible values are "plinear" for the Golub-Pereyra algorithm for partially linear least-squares models and "port" for the ‘nl2sol’ algorithm from the Port library – see the references.

それぞれのアルゴリズムについて調べるとっかかりも書かれているでしょう。

> qの値がマイナスになってしまいます

マイナスになってはいけないのでしょうか？
マイナスになってはいけないのにそうなるのは，データが悪いのでしょう。データは実際のものであるなら，個のデータはバズモデルに従わないということでしょう。
シンプレックス法で求めてもそのようになるので，このデータからはそういう結果になるのでしょうかね？

No.20350　Re: 非線形回帰のエラーについて　　【斜界人】　2013/10/20(Sun) 11:32

見落としてましたがsimplex関数でもm=102だし，その辺なのでしょう。しかし，私が勝手に考えた理屈が正しいとことにはならないです。最初に書きましたとおりモデルを理解しているわけではありません。

> qの値がマイナスになっている
q>0の制約があるなら青木先生の書いているとおりモデルかデータに問題があるのかもしれません。

No.20352　Re: 非線形回帰のエラーについて　　【工藤】　2013/10/21(Mon) 15:43

青木繁伸さん，斜界人さん

ご解答ありがとうございます。色々と調べてみたところ，マイナスになる事はよくあるそうです。制約条件を付けて再度計算したいと思います。

後，今までは，率を用いて非線形回帰を行いました。今回は，率ではなく売上で非線形回帰を行いたいと思いました。実際に以下のプログラムを入力したのですが，
Convergence failure: singular convergence (7)
という警告メッセージが出てきました。これはどういった意味なのでしょうか。ネットで調べても出てきませんでした・・・
以上，よろしくお願いします。
# デジカメ
Year <- 2003:2013
DR <- c(22246390, 28155724, 33571539, 30142998, 38103682, 47950455, 36563313, 25070662, 
    25918179, 19764168, 17250399)
n <- length(DR)
X1 <- DR[1:(n - 1)]
X2 <- X1^2
Y <- DR[2:n] - X1
W <- DR[1:n]
period <- 1:n

## バスモデルのパラメータの推定
M2 <- nls(W ~ m * (1 - exp(-(p + q) * period))/(1 + q/p * exp(-(p + q) * period)), 
    start = list(p = 0.01, q = 0.01, m = max(W)), trace = TRUE, algorithm = "port", 
    control = list(warnOnly = TRUE))

para <- M2$m$getPars()

## 推定したパラメータによる普及率の予測

p.hat <- para[1]
q.hat <- para[2]
m.hat <- para[3]

W.hat <- m.hat * (1 - exp(-(p.hat + q.hat) * period))/(1 + q.hat/p.hat * exp(-(p.hat + 
    q.hat) * period))

plot(Year, W.hat, type = "l", lty = 1, ylab = "sale")
lines(Year, W, lty = 2)
legend(2004, 23, c("Predicted", "Observed"), lty = 1:2)

summary(M2)

No.20355　Re: 非線形回帰のエラーについて　　【青木繁伸】　2013/10/21(Mon) 17:48

キチンとはっきりした回答はないかもしれないが，大まかなことは分かるはず。
例えば，以下の URL
http://tolstoy.newcastle.edu.au/R/help/06/01/19416.html
ようするに，データからモデルのパラメータを推定するには「情報」が少なすぎる。あるいは，そのデータからはそんなに多くのパラメータを含むモデルのパラメータは推定できない。

対処法は，もっと簡略化されたモデルを採用するか，データをもう少し集めること。

ということでは？

実際，あなたが使ったデータとモデルの予測値は大幅に異なっていますよね。とても，このモデルで予測できるものではないということでは？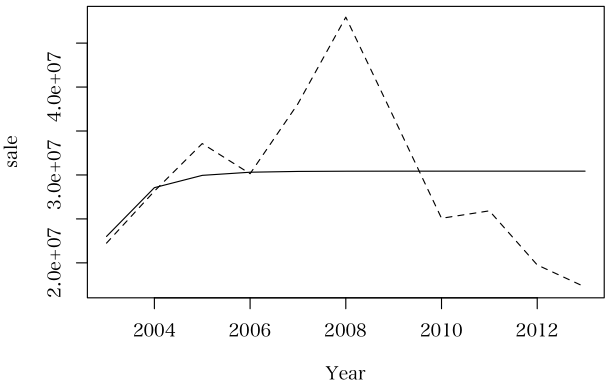

No.20356　Re: 非線形回帰のエラーについて　　【青木繁伸】　2013/10/21(Mon) 17:57

つづきですが。

あなたが使うべきデータは DR ではなく，cumsum(DR) ではないのですか？
DR は各年の売上ではないでしょうか？
バスモデルは，累積売上を予測するモデルではないですか？
インターネットなどで見たところでは，一つの図に，「各年の売上」と，「売上の累積の予測値」が描かれているのが多いようなので，あなたが勘違いしているのではないかなと，失礼ながら思った次第ですが。
> DR<-c(22246390,28155724,33571539,30142998,38103682,47950455,36563313,25070662,25918179,19764168,17250399)
> 
> DR <- cumsum(DR) # この一行を追加
というようにして実行すると，
> summary(M2)

Formula: W ~ m * (1 - exp(-(p + q) * period))/(1 + q/p * exp(-(p + q) * 
    period))

Parameters:
   Estimate Std. Error t value Pr(>|t|)
p 5.171e-02  2.372e-03   21.80 2.07e-08
q 3.294e-01  2.394e-02   13.76 7.50e-07
m 3.602e+08  8.050e+06   44.74 6.87e-11

Residual standard error: 3469000 on 8 degrees of freedom

Algorithm "port", convergence message: relative convergence (4)
のようになり，p も q も正の値になる。あてはめも良好というか，ぴったりな感じになりますが。

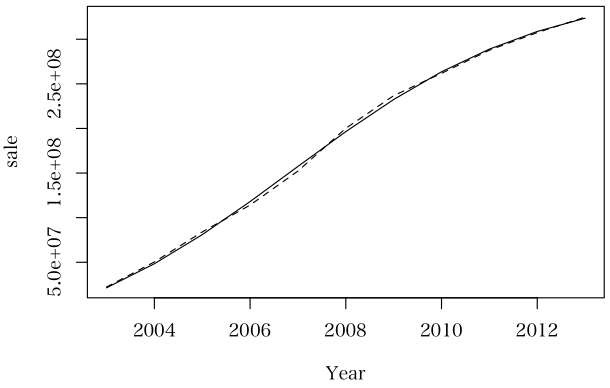
No.20357　Re: 非線形回帰のエラーについて　　【青木繁伸】　2013/10/21(Mon) 18:05

更につづきですが

最初の記事中のデータも，
> DR<-c(22.7,32.0,51.8,46.2,53.7,58.9,66.0,69.2,71.5,73.3,76.3,77.0)
> DR <- cumsum(DR)
とすれば，結果は
> summary(M2)

Formula: W ~ m * (1 - exp(-(p + q) * period))/(1 + q/p * exp(-(p + q) * 
    period))

Parameters:
   Estimate Std. Error t value Pr(>|t|)
p 2.199e-02  8.662e-04   25.38 1.10e-09
q 2.022e-01  1.265e-02   15.99 6.47e-08
m 1.213e+03  7.856e+01   15.44 8.78e-08

Residual standard error: 4.202 on 9 degrees of freedom

Number of iterations to convergence: 6 
Achieved convergence tolerance: 2.016e-06
となりますし，あてはめ図も，以下のようになりますけどね？？？？？？？

データの注釈では「普及率」と書かれているのですが，一箇所前年より［普及率」が低くなっているところ（51.8 から 46.2 に低下？）があるので，？？？？なんですけどね。

教科書などに載っている典型的なデータで，同じ結果になるかどうか確かめることをお勧めした方がよいのかなと思ったりしますが。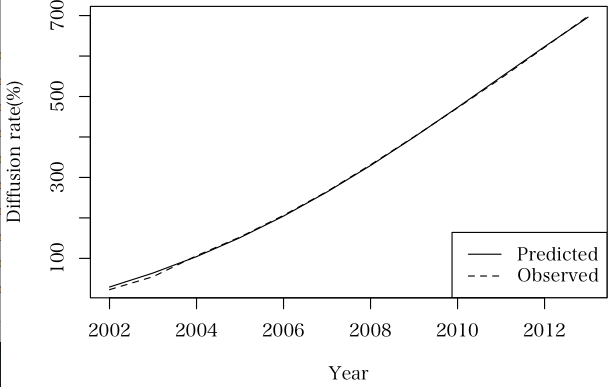

No.20367　Re: 非線形回帰のエラーについて　　【工藤】　2013/10/24(Thu) 00:56

青木繁伸様

ご回答ありがとうございます。

無事に問題を解決する事が出来ました。

本当にありがとうございました。