「統計学関連なんでもあり」の過去ログ--- 046

No.20097　ウィルコクソン符号付順位検定の結果の示し方　　【mii】　2013/07/24(Wed) 15:09

お世話になります。
2005年と2006年で同一対象者に，地域別に，エアコンの使用を開始する気温を調査しました。
何度で使用しますか，という問いをし，気温を整数（20℃など）で答えていただきました。

そして，2005年と2006年で使用開始気温に差があったのかを知るため，正規性がないのを確認し，対応のあるノンパラ検定，ウィルコクソン符号付順位検定を行いました。

有意差があった地域については，有意な変化があったと言えると思いますが，「変化があった」というだけではなく，具体的にどう変化したのか（開始気温が有意に上昇したのか低下したのか，○%増加した等）を述べるには，どうしたら良いでしょうか。

たとえば，26℃以上でのエアコンを使用開始する者が2005年では回答者のうち25.6％，2006年では25.1％だったとします。
ウィルコクソン符号付順位検定を行った結果，有意差があったとします。

2005年では26℃以上でエアコンを使用開始する者が25.6%だったが，2006年には25.1%で有意に減少した。

という風に，述べても良いのでしょうか。
すみませんが，ご返信よろしくお願い致します。

No.20098　Re: ウィルコクソン符号付順位検定の結果の示し方　　【mii】　2013/07/24(Wed) 16:53

追記で質問です。
http://aoki2.si.gunma-u.ac.jp/lecture/mb-arc/treatment.html
の下のほうにある対応のある線グラフをRで描くためのプログラムを教えて頂けますと幸いです。調べても箱ひげの作図例は出てくるのですが，このような図の描き方が出てきません。
よろしくお願い致します。

No.20099　Re: ウィルコクソン符号付順位検定の結果の示し方　　【青木繁伸】　2013/07/24(Wed) 17:17

> 対応のある線グラフをRで描くためのプログラム

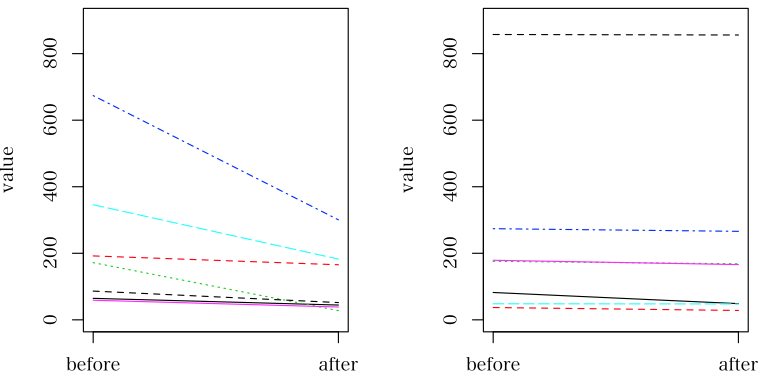
matplot 関数を使えばよいでしょう。
(d <- data.frame(
  before=c(64.6, 192.1, 171.9, 673.9, 346, 58.9, 86.4, 82.2, 37, 175.8, 273.9, 48.3, 179, 857.5),
  after=c(44.4, 165.5, 27.8, 300.6, 182.6, 38.4, 51.9, 48.7, 28.2, 168.5, 266, 47.8, 166, 856),
  treatment=rep(LETTERS[1:2], each=7)))
d2 <- split(d, d$treatment)
layout(matrix(1:2, 1))
invisible(lapply(d2, function(x) {
	matplot(t(x[1:2]), xaxt="n", ylim=c(0, 900), ylab="value", type="l")
	axis(1, at=1:2, labels=c("before", "after"))
}))
layout(1)

No.20100　Re: ウィルコクソン符号付順位検定の結果の示し方　　【青木繁伸】　2013/07/24(Wed) 17:18

> 2005年では26℃以上でエアコンを使用開始する者が25.6%だったが，2006年には25.1%で有意に減少した。

といいたいなら，対応のある比率の差の検定（マクネマー検定）を行えばよい。

No.20101　Re: ウィルコクソン符号付順位検定の結果の示し方　　【mii】　2013/07/24(Wed) 18:56

青木先生

ご返信ありがとうございます。
matplot関数のプログラムも教えて頂き大変助かります，ありがとうございます。

対応のある比率の差の検定（マクネマー検定）についてですが
理解不足のため，再度教えて下さい。
Temperature℃　2005number　2005percentage　2006number　2006percentage
20	9	0.7	1	0.1
21	5	0.4	0	0.0
22	36	2.9	7	0.6
23	53	4.2	37	3.0
24	65	5.2	79	6.3
25	156	12.5	101	8.1
26	131	10.5	204	16.3
27	165	13.2	354	28.4
28	321	25.7	380	30.4
29	58	4.6	60	4.8
30	249	20.0	25	2.0
total	1248	100.0	1248	100.0
上記データのとおり
2005,2006年とも同一対象者1248名からの回答を得ました。
20℃から30℃の間のエアコンの使用開始気温（Temperature）を答えていただき
それぞれの気温の人数（2005number,2006number）と，それぞれの年における割合(2005percentage,2006percentage)を算出しました。

このデータを用いて，26℃以上30℃以下で使用開始開始する者の割合（％）が2005年と2006年でどう変わったのかをマクネマー検定で知るには，どのようにRでプログラミングすれば良いでしょうか。

このようなデータではなく，元データが必要でしょうか。

大変お手数ですが，どうぞよろしくお願い致します。

No.20102　Re: ウィルコクソン符号付順位検定の結果の示し方　　【青木繁伸】　2013/07/24(Wed) 20:46

ウィルコクソンの符号順位和検定では，差があることしかいえません。
分類カテゴリーの変化をいうためにはマクネマー検定です。
カテゴリーが3個以上の場合は，マクネマー検定の拡張が必要です。正しい分割表を作るためには，集約データではなく元データが必要です。
http://aoki2.si.gunma-u.ac.jp/lecture/Hiritu/McNemar-test.html
の後半を参照してください。