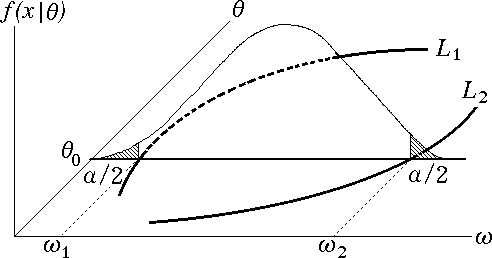
母数 $\theta$ を持つ母集団 $f ( x )$ から抽出された $n$ 標本から，統計量 $\omega_{n} = \omega(X_{1},\dots,X_{n})$ が計算されるとする。

　未知母数 $\theta$ の値を $\theta_{0}$ と定めれば $\omega_{n}$ の分布も一義的に決まる。

　つまり，$\omega_{n}$ の値が $\omega_{n} \lt \omega_{1} ，\omega_{n} \gt \omega_{2}$ となる確率は $\omega_{1} ，\omega_{2}$ により決まる。

　逆に，$\Pr\{\omega_{n} \lt \omega_{1}\}= \Pr\{\omega_{n} \gt \omega_{2}\}= \displaystyle \frac{\alpha}{2}$ となるように $\omega_{1} ，\omega_{2}$ を決めることもできる。

図 1．母数と統計量の関係

　図 2，3 中の曲線 $L_{1}$ と $L_{2}$ は対数正規分布の平均値を様々に変えたときに，分布の下側と上側の確率がそれぞれ $\displaystyle \frac{\alpha}{2} = 0.025$ である点の軌跡を結んだものである。

　$\theta_{0}$ が変化すると，$\alpha$ が与えられているとき $\omega_{1}$ ，$\omega_{2}$ が決まり，$L_{1}$ ，$L_{2}$ の曲線が得られる（図 2）。

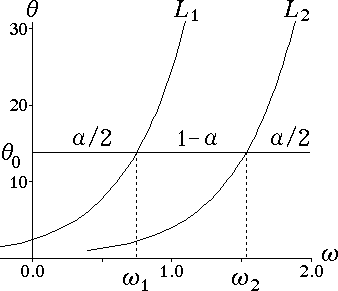図 2．母数と統計量の存在範囲（1）

　今度は逆に，ある $\omega_{0}$ が与えられると，$\theta = \theta_{U}$ のとき $\Pr\{\omega_{n} \lt \omega_{0}\} = \displaystyle \frac{\alpha}{2}$，$\theta=\theta_{L}$ のとき $\Pr\{\omega_{n} \gt \omega_{0}\} = \displaystyle \frac{\alpha}{2}$ となるような $\theta_{U} ，\theta_{L}$ が決まる（図 3）。

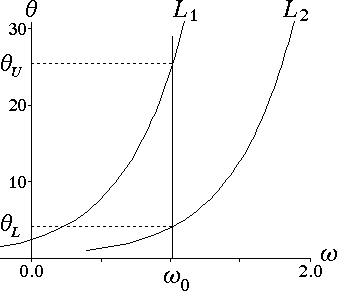図 3．母数と統計量の存在範囲（2）

　つまり，$\omega_{0}$ を $( 1 - \alpha )$ の確率で出現させる $\theta$ は，$\theta_{L} \lt \theta \lt \theta_{U}$ の範囲内にあることになる。

　この区間を $100\ ( 1 - \alpha ) \%$ 信頼区間 という。

　$100\ ( 1 - \alpha )$ を 信頼率 または 信頼係数 と呼ぶ。

　信頼率としては通常，$95\%$，$99\%$ などが用いられる。

演習問題−１：

　「ある機械で生産される製品から $n$ 個の製品を抽出したところ不良品が $m$ 個あった。この機械で作られる製品中の母不良率 $p$ の $100\ (1-\alpha)\%$ 信頼区間を求めよ。」

解答　　母比率の推定も参照せよ。

演習問題−２：

　「あるテレビ番組を見たかどうか 300 人に聞いたところ，30 人が見たと答えた。全国では何%が見たか，信頼率 $95\%$ で区間推定せよ。」

解答　　母比率の推定 も参照せよ。

応用問題：