1. 重回帰分析では，個々の説明変数は従属変数と直線相関関係にあることが仮定されている。個々の独立変数と従属変数の組合せで散布図を描き，直線相関から大幅にずれる独立変数は適当な変数変換をしてから用いた方がよい場合もある。

2. ステップワイズ変数選択によって独立変数の候補から自動的に重回帰式に取り入れる場合には，理論的に妥当な変数が必ずしも選択されないという不都合が生じる場合も多い。このような場合にはステップワイズ変数選択の結果を参考にして，変数選択を行わないで分析するのがよい。

3. 各変数が予測にどの程度寄与しているかを判断するためには，標準化偏回帰係数を見なければならない。

4. 回帰の分散分析の検定結果がどうであろうと，得られた予測式が実質的に有用かどうかの判断は，自由度調整済みの重相関係数の 2 乗に基づかなければならない。この値が 0.7 〜 0.8 程度以上でなければ，予測には役立たないであろう。このような場合には，従属変数を説明できる重要な変数が抜け落ちていないか検討する必要がある。

5. 予測値と標準化残差のプロット（ 残差分析 ）により，重回帰モデルの妥当性が検証できる。
   • 図 1 のように，予測値の大小にかかわらず標準化残差が一様に散らばっていれば重回帰モデルは妥当である。

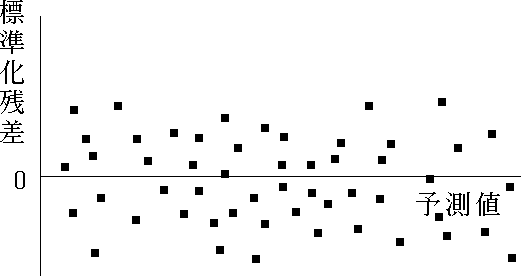     図 1．

   • 図 2 のように，データの中に外れ値がある場合には，数個の点が飛離れた位置にプロットされる。

     図 2．

   • 図 3 のように，予測値が大きく（ 小さく ）なるにつれ標準化残差の大きさが変化するような場合には分散が不均一であり，重回帰モデルが妥当でないことを表している。

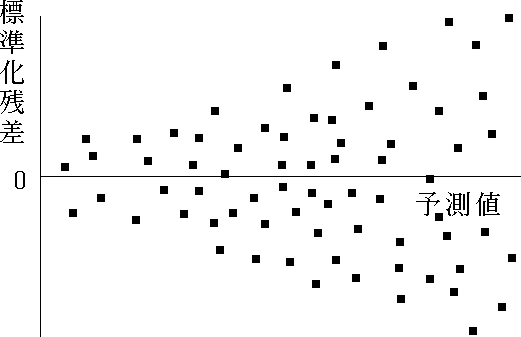     図 3．

   • 図 4 のように，標準化残差が曲線的な変動を見せるときは，独立変数と従属変数が曲線相関を示すので，なんらかの変数変換が必要であることを表す。

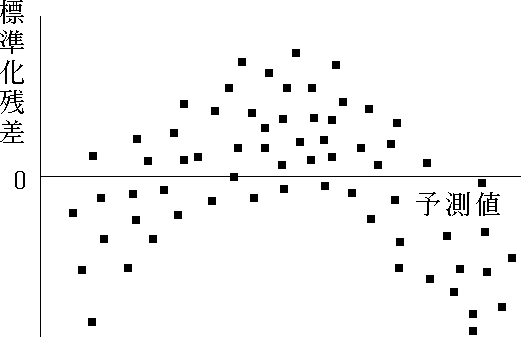     図 4．

演習問題：

応用問題：