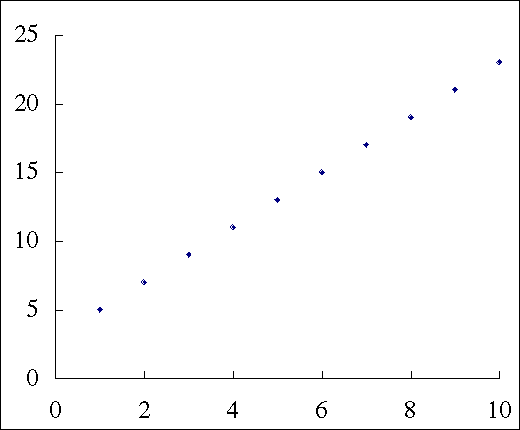
次の表のようなデータがあるとき，従属変数は独立変数の一次式で完全に予測できる。

　　　従属変数の予測値 = 3 + 2 $\times$ 独立変数

従属変数	独立変数
5	1
7	2
9	3
11	4
13	5
15	6
17	7
19	8
21	9
23	10

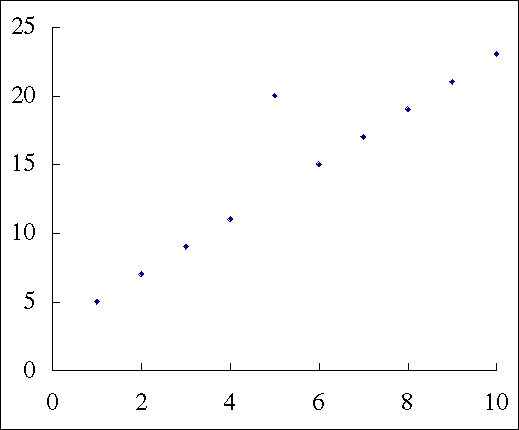
　しかし，次のようなデータにおいては，従属変数は独立変数だけでは予測できない。

従属変数	独立変数
5	1
7	2
9	3
11	4
20	5
15	6
17	7
19	8
21	9
23	10

　無理に直線回帰式に当てはめても，下図のようになるだけである。

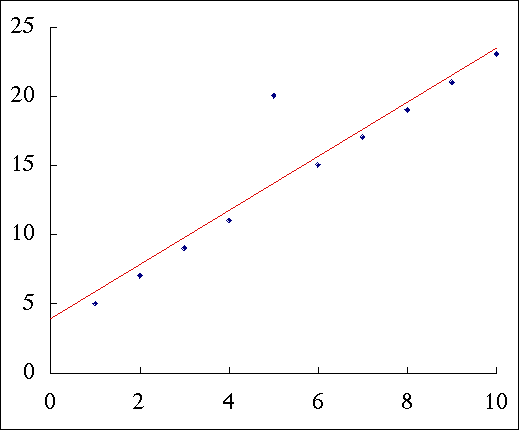
　予測がうまくいかない原因は，独立変数が 5 のときには，他の場合と違う「何らかの要因が作用しているらしい」ということである。

　そこで，この「何らかの要因」を表す独立変数を新たに導入する。

　この変数は，「何らかの要因」が存在するときに 1，存在しないときには 0 という値をとるものとする。

　すなわち，独立変数が 5 のときにこの変数は 1 となり，それ以外のときには 0 となる。

　このように，二つの値のうちのどちらかをとる（特に 0 か 1 かいずれかの値をとる）ような変数をダミー変数と呼ぶ。

従属変数	独立変数	ダミー変数
5	1	0
7	2	0
9	3	0
11	4	0
20	5	1
15	6	0
17	7	0
19	8	0
21	9	0
23	10	0

　このデータに対して重回帰分析を適用すると，以下のような結果が得られる。

	偏回帰係数	標準誤差	t 値	P 値
定数項	3	2.44456E-15	1.22722E+15	6.2998E-104
独立変数	2	3.86518E-16	5.1744E+15	2.6592E-108
ダミー変数	7	3.70063E-15	1.89157E+15	3.048E-105

　予測式として書くと，

　　　従属変数の予測値 = 3 + 2 $\times$ 独立変数 + 7 $\times$ ダミー変数

となる。

従属変数	独立変数	ダミー変数	予測値	独立変数の分	ダミー変数の分
5	1	0	5	5	0
7	2	0	7	7	0
9	3	0	9	9	0
11	4	0	11	11	0
20	5	1	20	13	7
15	6	0	15	15	0
17	7	0	17	17	0
19	8	0	19	19	0
21	9	0	21	21	0
23	10	0	23	23	0

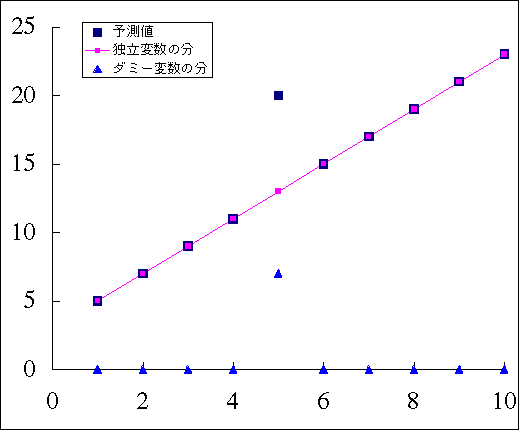
　独立変数が 5 のときには，ダミー変数が 1 であり，

　　　従属変数の予測値 = 3 + 2 $\times$ 独立変数 + 7 $\times$ ダミー変数

　　　　　　　　　　　= 3 + 2 $\times$ 5 + 7 $\times$ 1 = 20

になる。

すなわち，独立変数が 5 のときも，他のときと同じ予測式が成り立つとすると，

　　　従属変数の予測値 = 3 + 2 $\times$ 独立変数

　　　　　　　　　　　　= 3 + 2 $\times$ 5 = 13

となるところが，このときに「ある要因が働いた」ために +7 の効果が生じたのである。

　ダミー変数は 0 か 1 の値を取るのであるから，ダミー変数に対する偏回帰係数 7 を掛けると，要因が働くときに +7，働かないときには +0 ということになる。

　要因が複数ある場合には，それぞれの要因に対応するダミー変数を一個ずつ考えればよい。

　以下の図では，独立変数が 5 のときのほか，8 のときにも別の要因が作用しているようである。

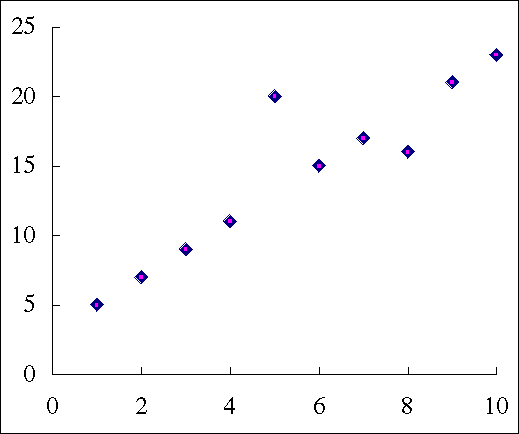
従属変数	独立変数	ダミー変数１	ダミー変数２
5	1	0	0
7	2	0	0
9	3	0	0
11	4	0	0
20	5	1	0
15	6	0	0
17	7	0	0
16	8	0	1
21	9	0	0
23	10	0	0

　このデータに対して重回帰分析を行うと，次のような結果が得られる。

	偏回帰係数
定数項	3
独立変数	2
ダミー変数１	7
ダミー変数２	-3

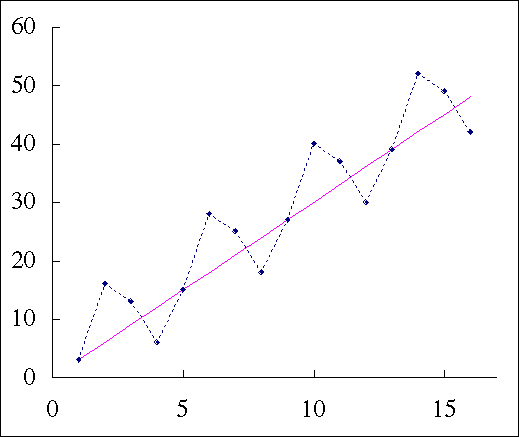
　このデータは，春夏秋冬の四半期ごとのデータをプロットしたものである。

　春を基準とすると紫の傾向線で示すような直線を引くことができる。この直線では，春に対する予測は完全に行える。夏と秋の予測については傾向線にプラス$\alpha$が，冬の予測についてはマイナス$\alpha$が必要である。

　予測に必要なダミー変数は，夏に対するダミー変数，秋に対するダミー変数，冬に対するダミー変数の三つである。

従属変数	独立変数	夏	秋	冬
3	1	0	0	0
16	2	1	0	0
13	3	0	1	0
6	4	0	0	1
15	5	0	0	0
28	6	1	0	0
25	7	0	1	0
18	8	0	0	1
27	9	0	0	0
40	10	1	0	0
37	11	0	1	0
30	12	0	0	1
39	13	0	0	0
52	14	1	0	0
49	15	0	1	0
42	16	0	0	1

　このデータを重回帰分析すると，以下のような結果が得られる。

	偏回帰係数
定数項	-6.89644E-15
独立変数	3
夏	10
秋	4
冬	-6

　すなわち，春のデータについては

　　　従属変数の予測値 = 3 $\times$ 独立変数

となり，夏に対しては「予測値 = 3 $\times$ 独立変数」で得られる予測値に +10，秋は +4，冬は -6 という修正項がつくのである。

　ちなみに，上の予測は，

　　　従属変数の予測値 = 定数項 + b1 $\times$ 独立変数 + b2 $\times$ 季節

ということになる。

　しかし，季節という変数が「春」，「夏」，「秋」，「冬」という 4 種類の値をとる「名義尺度」であるため，これでは重回帰分析に使用することができない。

　そこで，4 種類の値に対応して 4 個のダミー変数を考えることができる。

　ところで，本当に 4 個のダミー変数が必要かというとそうではない。

　図でもわかるように，どれか一つを基準とすれば残りの値はその基準に対して±αということで表現できるので，結局，ダミー変数は名義尺度の取る値の種類より 1 個少なくてすむのである。

　以下のようなデータについて回帰分析をしてみよう。ただし，独立変数は順序尺度である。

独立変数	従属変数
1	1
2	3
3	7
4	15

　本来はこのような場合には解析を行うのは不適切であるが，むりやり実行すると次のようになる。独立変数の 1, 2, 3, 4 というのが間隔尺度ではないということをおいても，回帰がうまくいっているとは思えない。

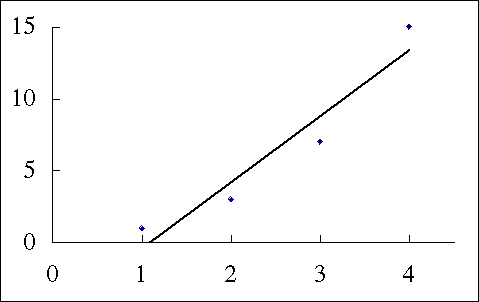
　そこで，独立変数がとる 4 種類の値に対応する 3 個のダミー変数を作成する。

ダミー変数1	ダミー変数2	ダミー変数3	従属変数
0	0	0	1
1	0	0	3
0	1	0	7
0	0	1	15

　重回帰分析の結果は以下のようになる。この重回帰式は，完全に 4 つのデータ点を通る（決定係数は 1 である）。

	偏回帰係数
定数項	1
ダミー変数1	2
ダミー変数2	6
ダミー変数3	14

　さて，重回帰式は

　　　従属変数 = 1+（2 $\times$ ダミー変数1）+（6 $\times$ ダミー変数2）+（14 $\times$ ダミー変数3）

であるが，たとえば，ダミー変数1は 0 か 1 の値しか取らないので，

　　　「2$\times$ダミー変数1」というのは，変数1 が 0 か 2 しかとらないものであると定義すると「重み（=1）$\times$変数1」と同じである。同じように，変数2は 0 か 6，変数3 は 0 か 14 しかとらない変数とすると，結局

　　　従属変数 = 1+（1 $\times$ 変数1）+（1 $\times$ 変数2）+（1 $\times$ 変数3）

　そして，変数1，変数2，変数3 は同時に0 以外の値はとらないので，もとの変数が値 1 をとるときに 0，値 1 のときに 2，値 3 のときに 6，値 4 のときに 14 となるような新しい独立変数を考える。すなわち，

元の変数	新しい変数	従属変数
1	0	1
2	2	3
3	6	7
4	14	15

のようになる。

　このデータに重回帰分析を適用すると，

	偏回帰係数
定数項	1
新しい変数	1

のようになり，この重回帰式（単回帰式）は 4 つの点全てを通る（決定係数は 1 である）。

　ここで示したのは「数量化 I 類」の考え方と同じになる。つまり，順序尺度の，たまたま適当な数値として表されたに過ぎない 1, 2, 3, 4 を数量化して，従属変数と直線関係になるように 0, 2, 6, 14 という数値を付与したのである。