偏回帰係数の求め方 Last modified: Aug 19, 2015
- 有効ケース数を $n$ とする。従属変数を $Y$,$p$ 個の独立変数を $X_{i}\ ( i = 1, 2, \dots , p)$ とする。
- 従属変数の予測値 $\hat{Y}$ は,定数を $b_0, b_1, b_2, \dots, b_p$ として,重回帰式 $\hat{Y} = b_0+b_1\ X_1+b_2\ X_2+\dots +b_p\ X_p$ により求められる。
- 以下では図 1 のような独立変数が $2$ 個の場合を考えることにする。
予測値 $\hat{Y}$ は予測平面 $\hat{Y} = b_0+b_1\ X_1+b_2\ X_2$ 上にある。
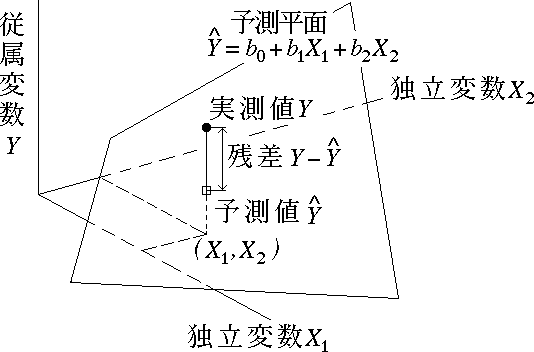 図 1.独立変数が $2$ 個のときの重回帰分析の模式図 |
- 実測値 $Y$ との差( 残差 )$e_i=Y_i-\hat{Y}_i$ を最小にすればよさそうであるが,残差は正負の符号を持つので,その $2$ 乗和が最小になるように独立変数にかけられる重み $b_{i}$( 偏回帰係数と呼ぶ )および定数項 $b_{0}$ を定める。具体的には,$(1)$ 式で示す $Q$ を最小にする係数 $b_0, b_1, b_2, \dots, b_p$ を求めるのである。
この手法を最小二乗法と呼び,得られる係数を最小二乗推定値と呼ぶ。
\[
\begin{align*}
Q & = \sum_{i=1}^n e_i^2 = \sum_{i=1}^n \left( Y_i-\hat{Y}_i \right)^2 \\[5pt]
& = \sum_{i=1}^n \left \{Y_i - (b_0+b_1\ X_{i1}+b_2\ X_{i2}) \right \}^2 \tag{1}
\end{align*}
\]
- まず,$(1)$ 式を,$b_{0}$,$b_{1}$,$b_{2}$ で偏微分して $0$ とおく。
\[
\left \{
\begin{eqnarray}
\frac{\partial Q}{\partial b_0} & = & -2 \sum_{i=1}^n \ \left \{ Y_i - (b_0+b_1\ X_{i1}+b_2\ X_{i2}) \right \} = 0 \\[5pt]
\frac{\partial Q}{\partial b_1} & = & -2 \sum_{i=1}^n \ X_{i1}\left \{ Y_i - (b_0+b_1\ X_{i1}+b_2\ X_{i2}) \right \} = 0 \\[5pt]
\frac{\partial Q}{\partial b_2} & = & -2 \sum_{i=1}^n \ X_{i2}\left \{ Y_i - (b_0+b_1\ X_{i1}+b_2\ X_{i2}) \right \} = 0
\end{eqnarray}
\right . \tag{2}
\]
- ( 2 )式に,変数 $Y$,$X_{1}$,$X_{2}$ の平均値を $\bar{Y}$,$\bar{X}_1$,$\bar{X}_2$ としたときの関係式
\[
b_0 = \bar{Y}-b_1\ \bar{X}_1-b_2\ \bar{X}_2 \tag{3}
\]
および,独立変数 $X_{i}$,$X_{j}$ 間の変動・共変動
\[
S_{ij} = \sum_{k=1}^n\ (X_{ki}-\bar{X}_i)\ (X_{kj}-\bar{X}_j)
\]
および,独立変数 $X_{i}$ と従属変数 $Y$ の共変動
\[
S_{iy} = \sum_{k=1}^n\ (X_{ki}-\bar{X}_i)\ (Y_{k}-\bar{Y})
\]
を代入して整理すると,
\[
\left \{
\begin{eqnarray}
b_1\ S_{11} + b_2\ S_{12} &=& S_{1y} \\[5pt]
b_1\ S_{21} + b_2\ S_{22} &=& S_{2y}
\end{eqnarray}
\right .
\]
という連立方程式( 正規方程式と呼ぶ )が得られる。
これを解くことにより偏回帰係数 $b_{1}$,$b_{2}$ が求まる。
- 一般的な表し方としては,
- 独立変数間の変動・共変動行列を $\mathbf{S}$,独立変数と従属変数間の共変動ベクトルを $\mathbf{c}$,偏回帰係数ベクトルを $\mathbf{b}$ として,$(4)$ 式のようになる。
\[
\mathbf{S\ b} = \mathbf{c} \tag{4}
\]
- $\mathbf{S}$ の逆行列を $\mathbf{S}^{ - 1}$ とすれば,偏回帰係数は $(5)$ 式で求められる。
\[
\mathbf{b} = \mathbf{S}^{-1}\ \mathbf{c} \tag{5}
\]
- 定数項 $b_{0}$ は $(3)$ 式から求められる。
- 重回帰分析の結果は,表 1 のようにまとめられる。
表 1.重回帰分析結果の表示
| 偏回帰係数 | 標準誤差 | $t$ 値 | $P$ 値 | 標準化偏回帰係数 |
| $X_{1}$ | 31.9670 | 6.840 | 4.673 | $\lt$ 0.001 | 0.620 |
| $X_{2}$ | 48.0183 | 12.322 | 3.897 | $\lt$ 0.001 | 0.478 |
| $X_{3}$ | $-$29.536 | 11.990 | 2.463 | 0.018 | $-$0.240 |
| $X_{4}$ | $-$454.373 | 171.514 | 2.649 | 0.011 | $-$0.284 |
| 定数項 | 594.562 | 789.895 | 0.753 | 0.456 |
|
$t$ 値の自由度は $42$
演習問題:
「表 2 のような,10 ケース,3 変数のデータおいて,変数 $X_{1}$,$X_{2}$ を用いて $Y$ を予測する重回帰式を求めなさい。」 答え
表 2.重回帰分析用のデータ
| $X_{1}$ | 1.2 | 1.6 | 3.5 | 4.0 | 5.6 | 5.7 | 6.7 | 7.5 | 8.5 | 9.7 |
| $X_{2}$ | 1.9 | 2.7 | 3.7 | 3.1 | 3.5 | 7.5 | 1.2 | 3.7 | 0.6 | 5.1 |
| $Y$ | 0.9 | 1.3 | 2.0 | 1.8 | 2.2 | 3.5 | 1.9 | 2.7 | 2.1 | 3.6 |
応用問題:
 次のページへ進む
次のページへ進む
 重回帰分析の最初のページへ戻る
重回帰分析の最初のページへ戻る
 E-mail to Shigenobu AOKI
E-mail to Shigenobu AOKI
