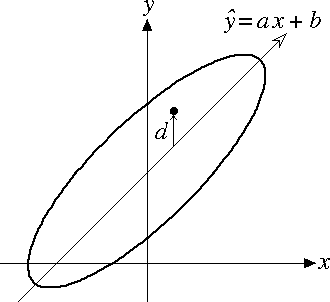重回帰分析の目的は，いくつかの変数に基づいて，別の変数を予測することである。

　単純にするために，一つの変数（ 独立変数 ）から別の変数（ 従属変数 ）を予測することを考える。

　独立変数を $x$，従属変数を $y$，$y$ の予測値を $\hat{y}$ としたとき，図 1 のような，各点の近くを通るような直線 $\hat{y} = a\ x+b$ が考えられる。

　この直線式の定数（$a$，$b$）は最小二乗法により求めることができる。

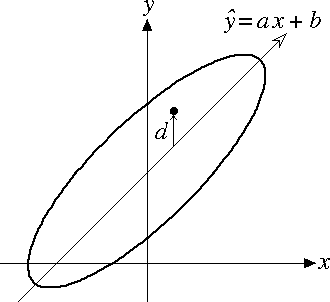図 1．回帰直線とは何か

　複数個の独立変数（$x_1, x_2, \dots, x_p$）がある場合には，定数を $b_0, b_1, b_2, \dots, b_p$ として，回帰式は一般的に $\hat{y} = b_0+b_1\ x_1+b_2\ x_2+\dots +b_p\ x_p$ のようになる。この式の右辺は合成変数の形になっていることがわかる。

演習問題：

応用問題：