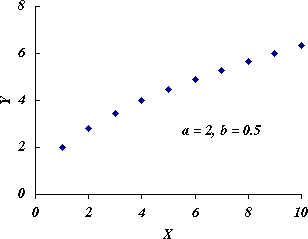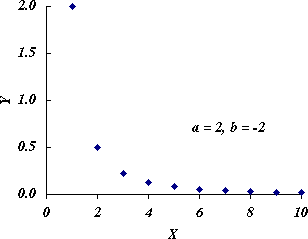例題：

　「表 1 のに示すようなデータに曲線をあてはめなさい。」

考え方：

1. 元のデータをプロットすると図 1 のようになる。

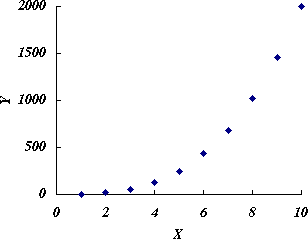   図 1．元データのプロット

2. $Y = a\ X^b$ の両辺の対数をとり，$\log Y = \log a + b\ \log X$ とする。

3. $c = \log a$，$V = \log Y$，$W = \log X$ とおいて，$V = c + b\ W$ なる直線回帰を行えばよい。

   これは，図 1 の縦軸と横軸を対数目盛りで描いたものが図 2 になる（データ点が直線上に並ぶ）ことを意味している。

   表 2．表 1 を変数変換したもの

   $W=\log X$	0.000	0.693	1.099	1.386	1.609	1.792	1.946	2.079	2.197	2.303
   $V=\log Y$	0.693	2.773	3.989	4.852	5.521	6.068	6.531	6.931	7.285	7.601

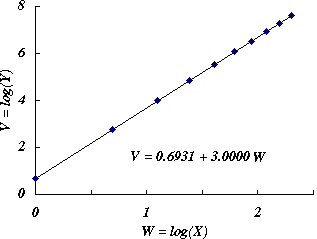   図 2．変数変換後のプロット

4. 求めるパラメータは，$a = \exp c$ となる。

   例題では，図 2 に示したように，$c = 0.6913$，$b = 3$ であるから，
   $a = \exp ( 0.6913 ) = 2$ となる（表 1 のデータは，この定数値に基づいて作成したものである）。

$b \gt 1$ のときは，図 1 のように，右上がりで下に凸の曲線になる。
$1 \gt b \gt 0$ のときは，図 3 のように，右上がりで上に凸の曲線になる。
$b \lt 0$ のときは，図 4 のように，右下がりで下に凸の曲線になる。

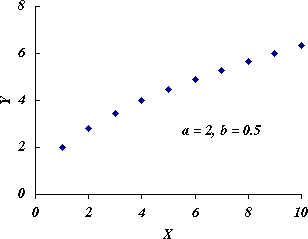図 3．$1 \gt b \gt 0$ のときの曲線の形		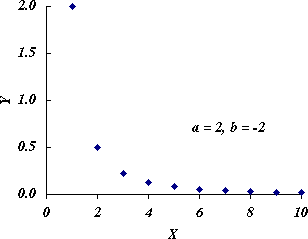図 4．$b \lt 0$ のときの曲線の形

R で計算してみる

演習問題：

応用問題：