直線回帰は重回帰分析の最も単純な場合である。

例題：

　「表 1 において，変数 $X$ を用いて，変数 $Y$ を予測する直線回帰式を求めなさい。」

計算手順：

1. 2 変数 $X$，$Y$ の観察値が $n$ 組あるとする。

   例題では，$n = 10$，$( X_{1} , Y_{1} ) = ( 2.8, 0.6 )$，$\dots$ ，$( X_{10} , Y_{10} ) = ( 13.4, 18.9 )$

2. 直線の傾き $a$ と切片 $b$ は，次式で求めることができる。 \[ \begin{align*} & a = \frac{\displaystyle \sum_{i=1}^n\ (X_i-\bar{X})\ (Y_i-\bar{Y})}{\displaystyle \sum_{i=1}^n\ (X_i-\bar{X})^2} \\[5pt] & b = \bar{Y}-a\ \bar{X} \end{align*} \] 　　例題では，以下のように計算を進める。 　　
   1. まず最初に，変数 $X$ と変数 $Y$ の平均値 $\bar{X}$ と $\bar{Y}$ を求める。
      　　 $\bar{X} = ( 2.8 + 3.4 + \dots + 13.4 )\ /\ 10 = 81.2\ /\ 10 = 8.12$
      　　 $\bar{Y} = ( 0.6 + 3.0 + \dots + 18.9 )\ /\ 10 = 98.5\ /\ 10 = 9.85$ 　　
   2. 次に，$a$ の計算式の分子になる「変数 $X$ と変数 $Y$ の共変動」を求める。
      　　 変数 $X$ と変数 $Y$ の共変動 $= { ( 2.8 - 8.12) \times ( 0.6 - 9.85 ) + \dots + ( 13.4 - 8.12) \times ( 18.9 - 9.85 ) } = 270.38$ 　　
   3. 次に，$a$ の計算式の分母になる「変数 $X$ の変動」を求める。
      　　 変数 $X$ の変動 $= { ( 2.8 - 8.12)^{2} + \dots + ( 13.4 - 8.12)^{2} } = 155.036$ 　　
   4. 以上から，$a = 270.38\ /\ 155.036 ≒ 1.744$ を得る。 　　
   5. また，$b = 9.85 - 1.744 \times 8.12 ≒ -4.311$ を得る。 　　
   6. よって，求める直線回帰式は$\hat{Y}= 1.744\ X - 4.311$ である。
      　　 図で示すと以下の通り。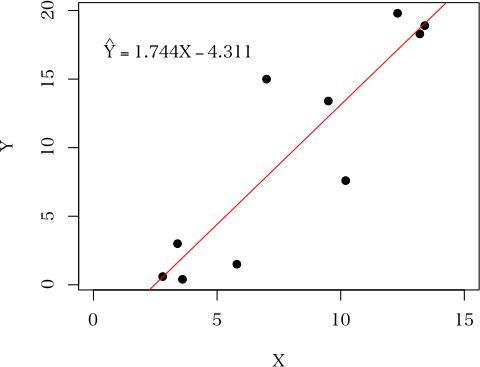

      図 1．直線回帰式

      　　

   　　R では以下のように計算する。

   	　　> X <- c(2.8, 3.4, 3.6, 5.8,  7.0,  9.5, 10.2, 12.3, 13.2, 13.4)
   	　　> Y <- c(0.6, 3.0, 0.4, 1.5, 15.0, 13.4,  7.6, 19.8, 18.3, 18.9)
   	　　> n <- length(x)
   	　　> Mean.X <- sum(X)/n # mean(X)
   	　　> Mean.Y <- sum(Y)/n # mean(Y)
   	　　> SS.XY <- sum((X-Mean.X)*(Y-Mean.Y)) # var(X, Y)*(n-1)
   	　　> SS.X <- sum((X-Mean.X)^2) # var(X)*(n-1)
   	　　> a <- SS.XY / SS.X
   	　　> b <- Mean.Y-a*Mean.X
   	　　> c(a=a, b=b)
   	　　        a         b 
   	　　 1.743982 -4.311134 
   	　　 
   	　　> ## 標準で用意されている lm 関数を使う場合
   	　　> ans <- lm(Y ~ X)
   	　　> summary(ans)
   	　　
   	　　Call:
   	　　lm(formula = Y ~ X)
   	　　
   	　　Residuals:
   	　　    Min      1Q  Median      3Q     Max 
   	　　-5.8775 -1.2778 -0.0651  1.3220  7.1033 
   	　　
   	　　Coefficients:
   	　　            Estimate Std. Error t value Pr(>|t|)
   	　　(Intercept)  -4.3111     2.7654  -1.559 0.157622
   	　　X             1.7440     0.3064   5.691 0.000459
   	　　
   	　　Residual standard error: 3.816 on 8 degrees of freedom
   	　　Multiple R-squared:  0.8019,	Adjusted R-squared:  0.7772 
   	　　F-statistic: 32.39 on 1 and 8 DF,  p-value: 0.000459
   	　　
   	　　# 散布図と回帰直線を描く
   	　　> plot(Y ~ X)
   	　　> abline(ans)
   	　　> text(5, 17, sprintf("Y.hat = %.3fX%.3f", a, b)) 
   

演習問題：

応用問題：