数量化 III 類 Last modified: Nov 07, 2002
カテゴリーデータに基づき,ケースおよび変数の似通ったものをまとめる。
分析に使用する変数が間隔尺度以上の場合の主成分分析に相当する。コレスポンデンス分析あるいは双対尺度法によるものと同じ結果が得られる。
また,ダミー変数を用いた主成分分析と関連がある。
分析に用いるデータには 2 種類ある。
- アイテムデータ
- 変数 $I_{i}\ ( i = 1, 2, \dots , p )$ が,それぞれ $m_{i}$ 個の選択肢を持つ。
- 各ケースは,表 1 に示すように,変数 $I_{i}$ の値として $1, 2, \dots , m_{i}$ の値を持つ。
- このデータを,1 個のアイテム変数 $I_{i}$ を $m_{i}$ 個のカテゴリー変数( $C_{ij};\ i = 1, 2, \dots , p;\ j = 1, 2, \dots , m_{i}$)に対応させ,アイテム変数のとる値が $j$ のとき $C_{ij} = 1$ で,それ以外のとき 0 をとるように,$\sum m_{i}$ 個のカテゴリーデータに展開する( 表 2 )。
- 各ケースあたりの「反応あり」のカテゴリー数は常に $p$ 個である。
表 1.アイテムデータの例
| ケース番号 | $I_{1}$ | $I_{2}$ | $I_{3}$ |
| 1 | 1 | 2 | 2 |
| 2 | 2 | 1 | 1 |
| 3 | 1 | 3 | 1 |
| 4 | 3 | 4 | 2 |
| 5 | 3 | 1 | 2 |
表 2.アイテムデータのカテゴリーデータへの展開
| ケース番号 | $I_{1}$ | | $I_{2}$ | | $I_{3}$ |
| $C_{11}$ | $C_{12}$ | $C_{13}$ | | $C_{21}$ | $C_{22}$ | $C_{23}$ | $C_{24}$ | | $C_{31}$ | $C_{32}$ |
| 1 | 1 | 0 | 0 | | 0 | 1 | 0 | 0 | | 0 | 1 |
| 2 | 0 | 1 | 0 | | 1 | 0 | 0 | 0 | | 1 | 0 |
| 3 | 1 | 0 | 0 | | 0 | 0 | 1 | 0 | | 1 | 0 |
| 4 | 0 | 0 | 1 | | 0 | 0 | 0 | 1 | | 0 | 1 |
| 5 | 0 | 0 | 1 | | 1 | 0 | 0 | 0 | | 0 | 1 |
- カテゴリーデータ
- 変数 $C_{i}\ ( i = 1, 2, \dots , p )$ が,それぞれ「反応あり」の場合に 1,「反応なし」の場合に 0 の値をとる。
- 表 3 に例を示したように,各ケースあたりの「反応あり」のカテゴリー数は一定ではない。
表 3.カテゴリーデータの例
| ケース番号 | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 2 | 0 | 1 | 1 | 0 | 1 |
| 3 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 | 0 |
アイテムデータも,分析に利用される時点ではカテゴリーデータに展開されるので,以下では表 3 の例を用いて説明する。
数量化 III 類では,表 3 の行と列を入れ替え,互いに似ているケースとカテゴリーが隣り合わせになるように配置しなおすことを目標とする。例えば,表 4 はそのようなものの 1 例である。これを見ると,対角線上に 1 が集まっていることがわかる。
表 4.カテゴリーデータの行と列の入れ替え例
| ケース番号 | $C_{1}$ | $C_{4}$ | $C_{3}$ | $C_{2}$ | $C_{5}$ |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
| 5 | 1 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 1 | 0 |
| 2 | 0 | 0 | 1 | 1 | 1 |
表 4 は,各ケースとカテゴリーを等間隔に配置する場合であるが,さらに,各ケースとカテゴリーにケースとカテゴリーは等間隔に配置される必要性はない。
そこで,ケースに割当てられる数値を $Y_{i}\ ( i = 1, 2, \dots , n )$ ,カテゴリーに割当てられる数値を $X_{j}\ ( j = 1, 2, \dots , p )$ とする。
全ケースの反応のあるカテゴリーについて $Y$ と $X$ の組合せを作る。
すなわち,表 4 の場合には,ケース 1 については $(Y_{1}, X_{1})$,$(Y_{1}, X_{3})$,$(Y_{1}, X_{4})$ の 3 組,ケース 3 については $(Y_{3}, X_{1})$,$(Y_{3}, X_{4})$ の 2 組などとなる。
全体でこのような $X$,$Y$ の組が $N$ 個あったとき,$X$ と $Y$ の相関が最も高くなるようにすれば $N$ 個の点は互に似ているもの同士が近くに配置されることになる。
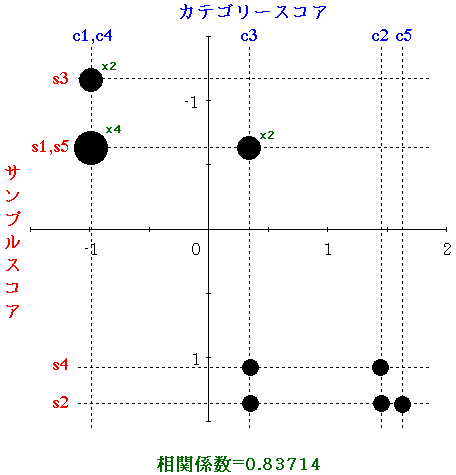
なお,ケースとカテゴリーの相関が高くなるような数値の与えかたは何通りか考えられるので,最も相関が高くなる場合,次に相関が高くなる場合 $\dots$ という具合に,何通りかの解が存在する。それぞれの解は互に他と直交する( 相関がない )ように選ばれるので,1 通りの解で解釈が十分できない場合には,いくつかの解を組合せて解釈するとよい。
補足説明
- 連続変数をカテゴリー化して用いる場合には,カテゴリー数が少なすぎないようにしなければならない( 多すぎても困る )。また,カテゴリー化は妥当な分割点で行ったほうがよい( 例えば 2 峰性データならその中点,正常範囲が決っているならその前後など )。
- アイテムデータはカテゴリーデータに変換できるが,両者は微妙な違いがある。
食べ物の好き嫌いを分析することを考えてみよう。調査票の作り方には 2 種類ある。
食べ物を列挙しておき,好きなものに ○ を付けさせる調査によって得られるのは,カテゴリーデータである。すなわち,$n$ 個のカテゴリーそれぞれに ○ がついていたかいなかったかであり,各被験者ごとに ○ の個数は異なる。
もう一つの方法は,食べ物について,「好き」,「嫌い」の二つの選択肢のいずれかに ○ を付けさせる方法である。この調査結果をデータファイル化する際には,アイテムデータとして入力することも,カテゴリーデータとして入力することも可能である。アイテムデータとして入力する場合は,この調査結果を,好きを 1,嫌いを 2 として入力する。$n$ 種類の食物に対して選択肢が 2 個ずつあるので,計 $2 n$ 個のカテゴリーデータに展開される。各被験者あたり ○ は $n$ 個あることになる。カテゴリーデータとして入力する場合は,前述の場合にならって,$n$ 個のカテゴリーデータとして,好きと答えた場合に 1,嫌いと答えた場合には 0 として入力する。各被験者あたり ○ の数は異なることになる。
分析結果( とその解釈 )も両者では異なったものになる。いずれの取り扱い方がよいかは一概にはいえないが,カテゴリーデータとして扱った場合に,嫌いという選択の情報を失うことになることや,もし後者の調査法で各項目の選択肢が 3 個以上であった場合との関連からいえば,アイテムデータとして取り扱った方がよいように思われる。両方の分析を行って比較してみるのが一番よい方法かもしれない。
- $p$ 個のアイテムデータを,$\sum m_{i}$ 個のカテゴリー変数に展開したダミー変数を用いて主成分分析を行うと,固有値が 0 でない主成分は $\sum ( m_{i} - 1 )$ 個得られる。この解は数量化 III 類の結果とよく似たものになる。
演習問題:
応用問題:
 計算プログラム [CGI(C)] [R] [Python]
計算プログラム [CGI(C)] [R] [Python]
 直前のページへ戻る
直前のページへ戻る  E-mail to Shigenobu AOKI
E-mail to Shigenobu AOKI

