箱髭図 Last modified: Jun 01, 2006
Tukey の箱髭図}は，図 1 のようなものである。
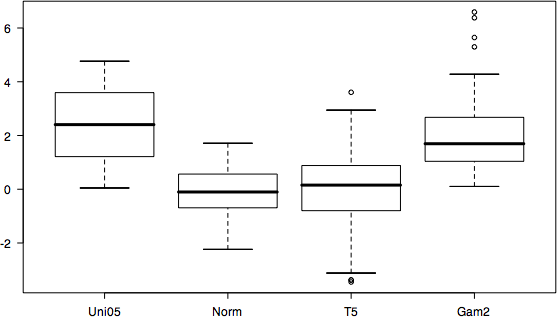 図 1．箱髭図の例 |
|---|
箱髭図は以下のようにして描かれる。
- 長方形の下側の辺は第1四分位数，上側の辺は第3四分位数である。
- 長方形の中央の線は中央値である。
- 長方形の下側の辺から伸びる点線の先端は，実際に存在するデータで「第1四分位数-1.5×IQR」より大きいデータ点である。
- 長方形の上側の辺から伸びる点線の先端は，実際に存在するデータで「第3四分位数+1.5×IQR」より小さいデータ点である。
- 「第1四分位数-1.5IQR」より小さいデータ点と，「第3四分位数+1.5IQR」より大きいデータは外れ値として 1 個ずつ記号で表示される。
注1： IQR とは，四分範囲のことである。
IQR = 第3四分位数-第1四分位数
注2： 長方形を平均値±標準偏差で描いたり，髭を最大値・最小値まで伸ばすという図が描かれる場合があるが，本来の箱髭図と混乱するので避ける方がよい。
注3： データの分布をより詳しく表示するにはいくつかの方法がある。
以下の 21 個のデータがある。これを箱髭図で表現してみよう。
59, 64, 41, 44, 58, 34, 63, 68, 51, 38, 66, 65, 41, 46, 61, 32, 54, 45, 67, 62, 100
- まず，小さい順に並べ，最小値，第1四分位数，中央値，第3四分位数，最大値の 5 つの要約値を求める
32, 34, 38, 41, 41, 44, 45, 46, 51, 54, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 100
- 最小値=32，第1四分位数=44，中央値=58，第3四分位数=64，最大値=100
- 四分範囲(IQR)=64-44=20
- 上側の髭は，実際に存在するデータ値で，64+1.5×20=94 より小さいもの，ということで 68
- 下側の髭は，実際に存在するデータ値で，44-1.5×20=14 より大きいもの，ということで 32
- 64+1.5×20=94 より大きいもの，44-1.5×20=14 より小さいものは 100 というデータ値 1 個である
注：R の fivenum 関数と quantile 関数は同じ 5 数要約値を返すが，定義が若干異なっており（quantile 関数は 9 通りものアルゴリズムをサポートしている），第1四分位数・第3四分位数については場合によっては両者の結果は一致しない。
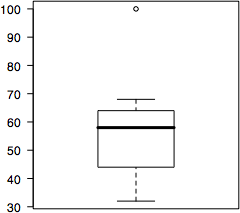 図 2．箱髭図 |
|---|
演習問題：
「表 1 のデータを箱髭図で表しなさい。」
表 1．箱髭図を描くデータ
| 0.84 | 1.05 | 1.13 | 1.26 | 1.54 |
| 0.86 | 1.05 | 1.14 | 1.26 | 1.57 |
| 0.90 | 1.06 | 1.16 | 1.28 | 1.62 |
| 0.92 | 1.06 | 1.17 | 1.33 | 1.66 |
| 0.93 | 1.07 | 1.18 | 1.35 | 1.74 |
| 0.98 | 1.08 | 1.19 | 1.35 | 1.87 |
| 1.01 | 1.09 | 1.20 | 1.35 | 2.00 |
| 1.02 | 1.10 | 1.22 | 1.39 |
|
| 1.03 | 1.12 | 1.23 | 1.42 |
|
| 1.04 | 1.13 | 1.24 | 1.46 |
|
|
問題1 中央値を求めなさい。答えを解答欄に記入し，送信ボタンをクリックしなさい。
問題2 第 1 四分位数を求めなさい。答えを解答欄に記入し，送信ボタンをクリックしなさい。
問題3 第 3 四分位数を求めなさい。答えを解答欄に記入し，送信ボタンをクリックしなさい。
問題4 箱髭図を描きなさい。
R による解答
応用問題：
直前のページへ戻る E-mail to Shigenobu AOKI