中央値（$M_e$）　　　　　Last modified: Mar 24, 2004

　測定値を小さい順に並べたとき，ちょうど真ん中にくる値である。分布の両端に大きな値や小さな値があっても影響されない（注）。

　有効ケース数を $n$，各ケースの測定値を $X_{i}\ ( i = 1，2，\dots ，n )$ とすると，以下の式で定義される。

\[ M_e = \left \{ \begin{align*} X_m, &　n \mbox{が奇数のとき，}m=\frac{n+1}{2} \\ \frac{X_m+X_{m+1}}{2}, &　n \mbox{が偶数のとき，}m=\frac{n}{2} \end{align*} \right . \] 　例題：「6 人の身長が 156.8，168.7，163.8，154.1，159.6，165.6 であった。中央値を求めよ。」

　解答：小さい順に並べると，154.1，156.8，159.6，163.8，165.6，168.7 になる。$m = \displaystyle \frac{6}{2} = 3$ ゆえ，3 番目と 4 番目のデータの平均値が中央値 $M_e$ である。よって $M_e = \displaystyle \frac{159.6 + 163.8}{2} = 161.7$ である。

One more step!

　しかし，同点があるときには上の式を直接使うと不適切な場合がある。

　例題： 22 個の測定値がある。中央値を求めよ。

　　　測定値：1，1，2，2，2，2，3，3，3，3，3，3，3，3，4，4，4，4，4，4，5，5

　解答：定義からいえば，中央値は 3 であるが，もう少しましな推定値を求めよう。

  1. まずデータ整理のために度数分布表を作る。
    測定値 度数 相対度数 累積度数 累積相対度数
    1 2 9.1 2 9.1
    2 4 18.2 6 27.3
    3 8 36.4 14 63.6
    4 6 27.3 20 90.9
    5 2 9.1 22 100.0
    合計 22 100.0

  2. 定義からいえば，中央値より小さいものは全体の 50%，大きいものは 50% あることになる。しかし，中央値 = 3 としたとき，3 より小さいものは 27.3%，大きいものは 36.4% あることになる。中央値は 3 以上，4 未満の値であるに違いない。

  3. 測定値 3 を持つ 8 個のデータは 2.5 以上，3.5 未満に 1 / 8 =　0.125 の間隔で均等に分布しているとすると，8 個のデータのもっともらしい値は，2.500，2.625，2.750，2.875，3.000，3.125，3.250，3.375 である。この中の 5 番目と 6 番目のデータの真ん中の値が中央値である。すなわち，$M_e = \displaystyle \frac{ 3.000 + 3.125 }{ 2 }= 3.0625$ となる。確かに 3.0625 より小さいデータは 11 個になることが確かめられる。

    注意：真の値が 2.5 以上，3.5 未満のとき，四捨五入されて測定値 3 が得られると考えるところがポイント。しかし，8 個のデータがその範囲に均等に分布する保証があるのか？とか，もっともらしい値が 2.500 から始まるのか？ということをつつけば問題もある。

　以上のことを一般化すると，以下のようになる。

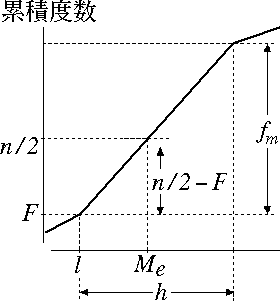
　$l$ を中央値のある級間の下限点，$F$ を $l$ 以下の累積度数，$f_{m}$ を中央値のある級間の度数，$h$ を級間の幅として，比例配分により次式を得る。

\[ M_e = l+\frac{\displaystyle \frac{n}{2}-F}{f_m}h \]

figure

　例題では，$n = 22$，$l = 2.5$，$F = 6$，$f_{m} = 8$，$h = 1$ ゆえ，$M_e = 3.125$ となる。

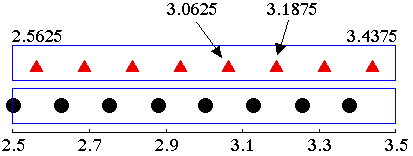
　注意：先の例では，$M_e = 3.0625$ であった。これは，8 つの同値のデータが下図の●のように分布しているとしたものである。しかし，▲のように分布していると考える方が一般的かもしれない。このようにすると▲は●より $0.125\ /\ 2 = 0.0625$ 大きい方向へずれている。従って，得られる中央値も，$M_e = \displaystyle \frac{3.0625+3.1876}{2}=3.125$ となり，上式による結果と一致する。

figure

演習問題：

　「426 人の女子学生の身長の度数分布は以下のようであった。」

表 1．女子学生の身長の度数分布
階級（単位 cm） 度数 相対度数 累積度数 累積相対度数
140 以上 145 未満 4 0.94 4 0.94
145 以上 150 未満 19 4.46 23 5.40
150 以上 155 未満 86 20.19 109 25.59
155 以上 160 未満 177 41.55 286 67.14
160 以上 165 未満 105 24.65 391 91.78
165 以上 170 未満 33 7.75 424 99.53
170 以上 175 未満 2 0.47 426 100.00
合計 426 100.00

問題1　測定精度は 0.1cm として，中央値を求めなさい。答えは小数点以下 3 桁目で四捨五入した値を解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

問題2　測定精度は無限小として，中央値を求めなさい。答えは小数点以下 3 桁目で四捨五入した値を解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

応用問題：

・ 計算プログラム　[CGI(AWK)]　[R]　[Python]
・ 直前のページへ戻る　　・ E-mail to Shigenobu AOKI