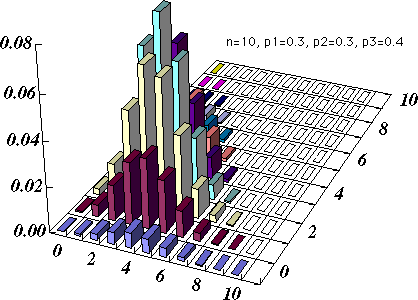
 図 1.多項分布の概形 |
|---|
$k$ 種類の事象が発生する確率をそれぞれ $p_{1}, p_{2}, \dots , p_{k},\ \ \left ( \displaystyle \sum_{i=1}^k p_{i} = 1 \right )$ としたとき,$n$ 回の試行によりそれぞれの事象が $x_{1}, x_{2}, \dots , x_{k}\ \left ( \displaystyle \sum_{i=1}^k x_{i} = n \right)$ 回おきる確率は次式で表される。 \[ f(x_{1}, x_{2}, \dots , x_{k-1}) = \frac{n!}{\displaystyle \prod_{i=1}^k x_i!}\ \prod_{i=1}^k p_i^{x_i} \]
 図 1.多項分布の概形 |
|---|
多項分布の平均 $E ( x_{i} )$ ,分散 $V ( x_{i} )$ は
\[ E ( x_{i} ) = n p_{i},\ V ( x_{i} ) = n p_{i} ( 1 - p_{i} ) \] である。
$k = 2$ のときは二項分布である。
観察値を $n_i$,期待値を $m_{i} = n\ p_{i},\ \ ( i = 1, 2, \dots , k )$ とし,$m_{i}$,$n_i$ が十分大きいとき,変量 $\chi^2 = \displaystyle \sum_{i=1}^k \frac{( n_i - m_{i} ) ^{2}} {m_{i}}$ は,近似的に自由度 $k - 1$ の $\chi^2$ 分布に従う。
演習問題:
応用問題: