$\chi^2$ 分布表　上側確率の計算　パーセント点の計算

　$\mathcal{N}(0, 1^2)$ 分布すなわち，平均値が 0，分散 1 の標準正規分布に従う $n$ 個の独立な確率変数 $x_{i}$ があるとき，その平方和 $\chi^2 = x_{1}^2 + x_{2}^{2} + … + x_{n}^{2}$ はまた，ひとつの確率変数である。この分布は，自由度 $\phi = n$ の $\chi^2$ 分布 と呼ばれる。 　\[ 　 f_{\phi}(\chi^2) = \frac{(\chi^2)^{\phi/2-1}\ e^{-\chi^2/2}} {2^{\phi/2}\ \Gamma(\phi/2)},\ \chi^2 \geqq 0 　\] 　$\Gamma ( x )$ はガンマ関数である。

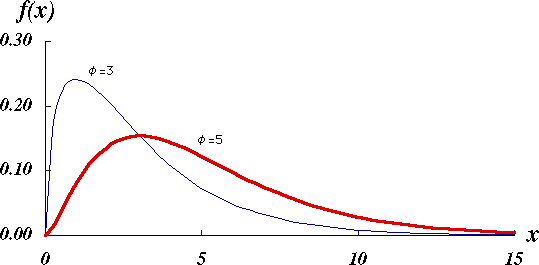図 1．$\chi^2$ 分布の概形

　平均 $E ( \chi^2 )$ ，分散 $V ( \chi^2 )$ は \[ 　 E ( \chi^2 ) = \phi，　V ( \chi^2 ) = 2 \phi \] である。

演習問題：

応用問題：