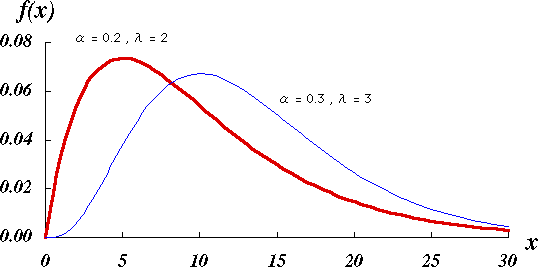
 図 1.ガンマ分布の概形 |
|---|
\[ f(x) = \frac{1}{\Gamma(\lambda)}\ \alpha^\lambda\ x^{\lambda-1}\ e^{-\alpha\ x},\ 0 \lt x \lt \infty,\ \lambda \geqq 0 \] $\Gamma ( \lambda )$ はガンマ関数である。
 図 1.ガンマ分布の概形 |
|---|
この分布で,$\lambda = 1$ のときは,$f ( x ) = \alpha e^{ - \alpha\ x}$ となり,これは指数分布である。
平均 $E ( x ) $,分散 $V ( x )$ は
\[ E ( x ) = \frac{\lambda}{\alpha},\ V ( x ) = \frac{\lambda}{\alpha^{2}} \] である。
演習問題:
応用問題: