判別分析（線形判別関数） Last modified: Aug 27, 2009
目的
線形判別分析を行う。
変数選択を行う場合には「sdis 関数」を使うこと。
（R の MASS パッケージに lda, predict.lda がある）
使用法
disc(data, group, func.name=c("solve", "ginv"))
print.disc(obj, digits=5)
summary.disc(obj, digits=5)
plot.disc(obj, which=c("boxplot", "barplot"), nclass=20, ...)
引数
data データ行列（行がケース，列が変数）
group 各ケースがどの群であるかを表す変数
func.name 逆行列を計算する関数名（solve か ginv）。
普通に逆行列が求まる場合にはどちらを使っても結果は同じ
省略時は solve
ムーア・ペンローズ型一般化逆行列を使うときは ginv
obj disc 関数が返すオブジェクト
digits 結果の表示桁数
which 2 群判別の場合に，描画するグラフの種類
nclass barplot のときのおよその階級数
pch scatterplot を描く記号
col scatterplot の記号の色
xpos, ypos scatterplot の凡例の位置
... boxplot, barplot, scatterplot に引き渡す引数
ソース
インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/disc.R", encoding="euc-jp")
# 線形判別関数
disc <- function( data, # データ行列
group, # 群変数
func.name=c("solve", "ginv")) # 逆行列を計算する関数名
{
inverse <- if (match.arg(func.name) == "solve") solve else { library(MASS); ginv}
data <- as.data.frame(data)
if (is.null(colnames(data))) {
colnames(data) <- paste("Var", 1:p, sep="")
}
vname <- colnames(data)
group <- as.factor(as.matrix(group)) # factor にする
gname <- levels(group)
OK <- complete.cases(data, group) # 欠損値を持つケースを除く
data <- as.matrix(data[OK,])
group <- group[OK]
p <- ncol(data) # 説明変数の数
ncase <- nrow(data) # サンプルサイズ
num <- table(group) # 各群のサンプルサイズ
ng <- length(num) # 群の数
g.name <- names(num) # 群の名前
means <- t(matrix(unlist(by(data, group, colMeans)), p))
g.mean <- colMeans(data)
t <- var(data)*(ncase-1) # 分散共分散行列
vars <- by(data, group, function(x) var(x)*(nrow(x)-1)) # 各群の変動・共変動行列
w <- matrix(rowSums(matrix(mapply("+", vars), ncol=ng)), p) # 群内変動・共変動行列
g.sd <- apply(data, 2, sd) # 各変数の標準偏差
det.w <- det(w) # 行列式
det.t <- det(t) # 行列式
wl <- det.w/det.t
inv.w <- inverse(w) # 逆行列
a <- -2*(ncase-ng)*inv.w%*%t(means)
a0 <- rowSums(means%*%inv.w*means)*(ncase-ng)
c.function <- rbind(a, a0)
temp <- matrix(0, nr=ng, nc=ng)
temp1 <- row(temp)
temp1 <- temp1[upper.tri(temp1)]
temp2 <- col(temp)
temp2 <- temp2[upper.tri(temp2)]
d.function <- sapply(1:length(temp1), function(i) (c.function[,temp2[i]]-c.function[,temp1[i]])/2)
F <- diag(inverse(t)/inv.w)
idf1 <- ng-1 # 第一自由度
idf2 <- ncase-idf1-p # 第二自由度
F <- idf2/idf1*(1-F)/F # F 値
P <- pf(F, idf1, idf2, lower.tail=FALSE) # P 値
c1 <- ifelse(p^2+idf1^2 != 5, sqrt((p^2*idf1^2-4)/(p^2+idf1^2-5)), 1)
c2 <- wl^(1/c1)
df1 <- p*idf1
df2 <- (ncase-1-(p+ng)/2)*c1+1-0.5*p*idf1
F.wl <- df2*(1-c2)/(df1*c2)
P.wl <- pf(F.wl, df1, df2, lower.tail=FALSE)
t.data <- t(data)
D2 <- (ncase-ng)*matrix(sapply(1:ng, function(i) {temp <- t.data-means[i,]; sapply(1:ncase, function(j) temp[,j]%*%inv.w%*%temp[,j])}), nr=ncase)
P2 <- pchisq(D2, p, lower.tail=FALSE)
prediction <- as.factor(g.name[apply(P2, 1, order)[ng,]])
correct <- ifelse(prediction == group, TRUE, FALSE)
correct.table <- table(group, prediction)
correct.rate <- sum(diag(correct.table))/ncase*100
factor1 <- levels(group)
factor2 <- levels(prediction)
if (ng ==2) { # 2 群の場合には，判別値を計算
discriminant.value <- data%*%d.function[1:p]+d.function[p+1]
}
else {
discriminant.value <- NULL
}
colnames(c.function) <- paste("g", 1:ng, sep="")
colnames(D2) <- paste("D to", gname)
colnames(P2) <- paste("P to", gname)
colnames(d.function) <- paste(gname[temp1], gname[temp2], sep=":")
rownames(c.function) <- rownames(d.function) <- c(vname, "constant")
colnames(c.function) <- gname
return(structure(list(d.function=d.function, c.function=c.function, partial.F=F, partial.F.P=P, df1=idf1, df2=idf2, wilks.lambda=wl, wilks.lambda.F=F.wl, wilks.lambda.P=P.wl, wilks.lambda.df1=df1, wilks.lambda.df2=df2, distance=D2, P.value=P2, prediction=prediction, correct=correct, correct.table=correct.table, correct.rate=correct.rate, discriminant.value=discriminant.value, group=group, factor1=factor1, factor2=factor2), class="disc"))
}
# print メソッド
print.disc <- function( obj, # disc 関数が返すオブジェクト
digits=5) # 結果の表示桁数
{
cat("\n判別関数\n\n")
result <- cbind(obj$d.function, "Partial F"=c(obj$partial.F, NA), "p-value"=c(obj$partial.F.P, NA))
print.default(round(result, digits=digits), na.print="")
cat("\n分類関数\n\n")
print(round(obj$c.function, digits=digits))
cat("\n判別結果\n\n")
print(obj$correct.table)
cat(sprintf("\n正判別率 = %.1f %%\n", obj$correct.rate))
}
# summary メソッド # すべての結果を表示する
summary.disc <- function( obj, # disc が返すオブジェクト
digits=5) # 結果の表示桁数
{
print.default(obj, digits=digits)
}
# plot メソッド
plot.disc <- function( obj, # disc 関数が返すオブジェクトの
which=c("boxplot", "barplot", "scatterplot"), # 箱髭図か棒グラフか散布図かの選択
nclass=20, # 棒グラフの場合のおよその階級数
pch=1:ncol(obj$distance), # scatterplot を描く記号
col=1:ncol(obj$distance), # scatterplot の記号の色
xpos="topright", ypos=NULL, # scatterplot の凡例の位置
...) # boxplot, barplot, scatterplt に引き渡す引数
{
if (!is.null(obj$discriminant.value)) {
which <- match.arg(which)
if (which == "boxplot") { # boxplot
plot(obj$discriminant.value ~ obj$group, xlab="群", ylab="判別値", ...)
}
else if (which == "barplot") { # barplot
tbl <- table(obj$group, cut(obj$discriminant.value,
breaks=pretty(obj$discriminant.value, n=nclass)))
barplot(tbl, beside=TRUE, legend=TRUE, xlab="判別値", ...)
}
else { # scatterplot 各群の重心までの二乗距離
group <- obj$group
group.levels <- levels(group)
distance1 <- obj$distance[,1]
distance2 <- obj$distance[,2]
max1 <- max(distance1)
max2 <- max(distance2)
max0 <- max(max1, max2)
plot(distance1, distance2, col=col[as.integer(group)], pch=pch[as.integer(group)],
xlim=c(0, max0), xlab=paste(group.levels[1], "の重心への二乗距離"),
ylim=c(0, max0), ylab=paste(group.levels[2], "の重心への二乗距離"), asp=1, ...)
abline(0, 1, lty=2)
text(max1, max2/2, paste(group.levels[2], "に判別される領域"), pos=2)
text(0, max2+strheight("H")*1.5, paste(group.levels[1], "に判別される領域"), pos=4)
legend(x=xpos, y=ypos, legend=group.levels, col=col, pch=pch)
}
}
else {
warning("3群以上の場合にはグラフ表示は用意されていません")
}
}
使用例
> data(iris) # Fisher のアヤメのデータ
print メソッドによる出力
> ( result <- disc(iris[1:4], iris[5]) )
判別関数
setosa:versicolor setosa:virginica versicolor:virginica Partial F p-value
Sepal.Length 7.84596 11.09832 3.25236 4.72115 0.01033
Sepal.Width 16.51536 19.90259 3.38723 21.93593 0.00000
Petal.Length -21.64209 -29.19718 -7.55509 35.59017 0.00000
Petal.Width -23.83264 -38.47752 -14.64488 24.90433 0.00000
constant -13.45586 18.05985 31.51571
分類関数
setosa versicolor virginica
Sepal.Length -47.08833 -31.39642 -24.89170
Sepal.Width -47.17574 -14.14502 -7.37056
Petal.Length 32.86128 -10.42290 -25.53309
Petal.Width 34.79682 -12.86846 -42.15823
constant 170.41972 143.50799 206.53942
判別結果
prediction
group setosa versicolor virginica
setosa 50 0 0
versicolor 0 48 2
virginica 0 1 49
正判別率 = 98.0 %
summary メソッドによる出力
> summary(result)
$d.function # 判別関数
setosa:versicolor setosa:virginica versicolor:virginica
Sepal.Length 7.846 11.098 3.2524
Sepal.Width 16.515 19.903 3.3872
Petal.Length -21.642 -29.197 -7.5551
Petal.Width -23.833 -38.478 -14.6449
constant -13.456 18.060 31.5157
$c.function # 分類関数
setosa versicolor virginica
Sepal.Length -47.088 -31.396 -24.8917
Sepal.Width -47.176 -14.145 -7.3706
Petal.Length 32.861 -10.423 -25.5331
Petal.Width 34.797 -12.868 -42.1582
constant 170.420 143.508 206.5394
$partial.F # 偏 F 値
Sepal.Length Sepal.Width Petal.Length Petal.Width
4.7212 21.9359 35.5902 24.9043
$partial.F.P # 偏 F 値に対する P 値
Sepal.Length Sepal.Width Petal.Length Petal.Width
1.0329e-02 4.8312e-09 2.7562e-13 5.1432e-10
$df1 # 偏 F 値の自由度
[1] 2
$df2 # 偏 F 値の自由度
[1] 144
$wilks.lambda # ウィルクスのΛ
[1] 0.023439
$wilks.lambda.F # ウィルクスのΛと等価な F 値
[1] 199.15
$wilks.lambda.P # ウィルクスのΛと等価な F 値に対する P 値
[1] 1.365e-112
$wilks.lambda.df1 # ウィルクスのΛと等価な F 値の自由度
[1] 8
$wilks.lambda.df2 # ウィルクスのΛと等価な F 値の自由度
[1] 288
$distance # 各ケースから各重心へのマハラノビスの距離の二乗
D to setosa D to versicolor D to virginica
[1,] 0.29109 98.88475 191.78864
[2,] 2.03135 80.97126 169.18698
[3,] 0.55328 87.28938 177.07006
[4,] 2.08670 75.29369 160.72442
[5,] 0.59563 100.92317 193.85404
[6,] 1.94475 95.93997 183.11405
[7,] 1.33369 84.01179 170.05690
[8,] 0.11741 89.51039 179.57534
[9,] 3.85012 71.64100 155.92692
[10,] 1.44194 84.12304 174.43416
中略
[148,] 158.98165 12.75125 1.23422
[149,] 188.87498 28.19287 5.62524
[150,] 153.76185 11.97777 3.92688
$P.value # 各ケースが各群に属する確率
P to setosa P to versicolor P to virginica
[1,] 9.9038e-01 1.6992e-20 2.1874e-40
[2,] 7.2999e-01 1.0845e-16 1.5630e-35
[3,] 9.6811e-01 4.9559e-18 3.1748e-37
[4,] 7.1982e-01 1.7270e-15 1.0223e-33
[5,] 9.6355e-01 6.2560e-21 7.8711e-41
[6,] 7.4592e-01 7.1917e-20 1.5984e-38
[7,] 8.5563e-01 2.4581e-17 1.0168e-35
[8,] 9.9834e-01 1.6730e-18 9.1989e-38
[9,] 4.2667e-01 1.0220e-14 1.0923e-32
[10,] 8.3687e-01 2.3281e-17 1.1686e-36
中略
[148,] 2.4172e-33 1.2557e-02 8.7243e-01
[149,] 9.2478e-40 1.1399e-05 2.2894e-01
[150,] 3.1803e-32 1.7517e-02 4.1599e-01
$prediction # 各ケースがどの群に属するかの判定
[1] setosa setosa setosa setosa setosa setosa setosa setosa
[9] setosa setosa setosa setosa setosa setosa setosa setosa
[17] setosa setosa setosa setosa setosa setosa setosa setosa
[25] setosa setosa setosa setosa setosa setosa setosa setosa
[33] setosa setosa setosa setosa setosa setosa setosa setosa
[41] setosa setosa setosa setosa setosa setosa setosa setosa
[49] setosa setosa versicolor versicolor versicolor versicolor versicolor versicolor
[57] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[65] versicolor versicolor versicolor versicolor versicolor versicolor virginica versicolor
[73] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[81] versicolor versicolor versicolor virginica versicolor versicolor versicolor versicolor
[89] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[97] versicolor versicolor versicolor versicolor virginica virginica virginica virginica
[105] virginica virginica virginica virginica virginica virginica virginica virginica
[113] virginica virginica virginica virginica virginica virginica virginica virginica
[121] virginica virginica virginica virginica virginica virginica virginica virginica
[129] virginica virginica virginica virginica virginica versicolor virginica virginica
[137] virginica virginica virginica virginica virginica virginica virginica virginica
[145] virginica virginica virginica virginica virginica virginica
Levels: setosa versicolor virginica
$correct # 判定が正しいかどうか
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[16] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[31] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[46] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[61] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE FALSE TRUE TRUE TRUE TRUE
[76] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE FALSE TRUE TRUE TRUE TRUE TRUE TRUE
[91] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[106] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[121] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE FALSE TRUE
[136] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
$correct.table # 判別結果の総括表
prediction
group setosa versicolor virginica
setosa 50 0 0
versicolor 0 48 2
virginica 0 1 49
$correct.ratio # 正判別率
[1] 98
$discriminant.value # 判別値（2 群の判別のときのみ）
NULL
$group # 実際の群
[1] setosa setosa setosa setosa setosa setosa setosa setosa
[9] setosa setosa setosa setosa setosa setosa setosa setosa
[17] setosa setosa setosa setosa setosa setosa setosa setosa
[25] setosa setosa setosa setosa setosa setosa setosa setosa
[33] setosa setosa setosa setosa setosa setosa setosa setosa
[41] setosa setosa setosa setosa setosa setosa setosa setosa
[49] setosa setosa versicolor versicolor versicolor versicolor versicolor versicolor
[57] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[65] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[73] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[81] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[89] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[97] versicolor versicolor versicolor versicolor virginica virginica virginica virginica
[105] virginica virginica virginica virginica virginica virginica virginica virginica
[113] virginica virginica virginica virginica virginica virginica virginica virginica
[121] virginica virginica virginica virginica virginica virginica virginica virginica
[129] virginica virginica virginica virginica virginica virginica virginica virginica
[137] virginica virginica virginica virginica virginica virginica virginica virginica
[145] virginica virginica virginica virginica virginica virginica
Levels: setosa versicolor virginica
$factor1 # group に与えられたデータ
[1] "setosa" "versicolor" "virginica"
$factor2
[1] "setosa" "versicolor" "virginica"
二群の判別の場合のグラフ表示
> (ans <- disc(iris[51:150, 1:4], iris[51:150, 5]))
判別関数
versicolor:virginica Partial F p-value
Sepal.Length 3.5563 7.3679 7.8862e-03
Sepal.Width 5.5786 10.5875 1.5776e-03
Petal.Length -6.9701 24.1566 3.7035e-06
Petal.Width -12.3860 37.0916 2.3836e-08
constant 16.6631
分類関数
versicolor virginica
Sepal.Length -30.8020 -23.689
Sepal.Width -31.9428 -20.786
Petal.Length 5.1633 -8.777
Petal.Width 1.1729 -23.599
constant 123.8859 157.212
判別結果
prediction
group versicolor virginica
versicolor 48 2
virginica 1 49
正判別率 = 97.0 %
> plot(ans)
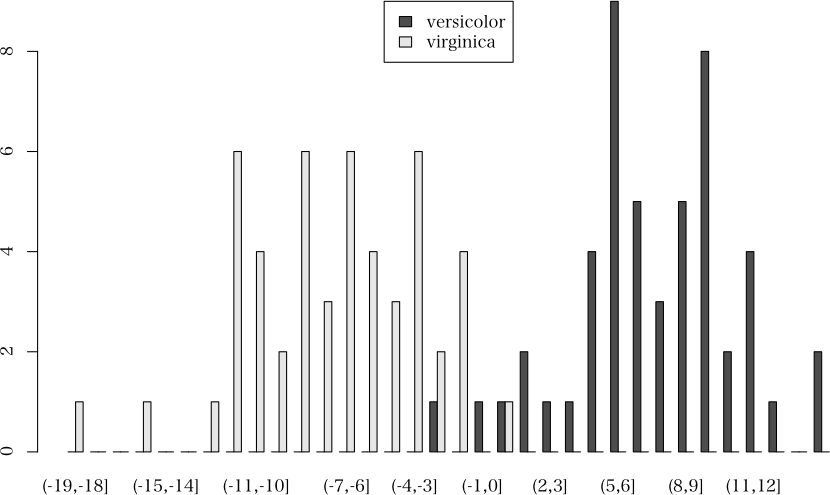
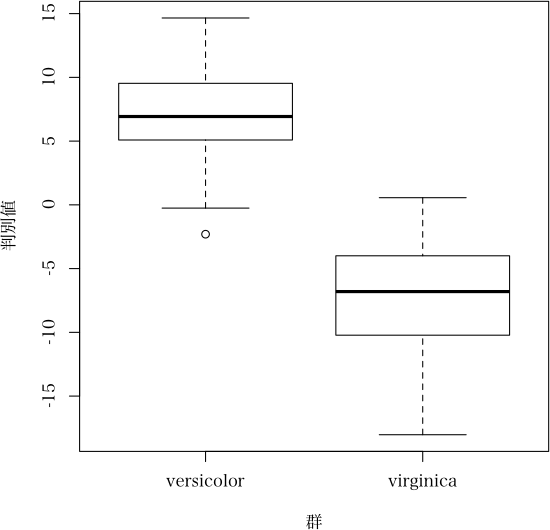> plot(ans, which="barplot", nclass=40, args.legend=list(x="top"))
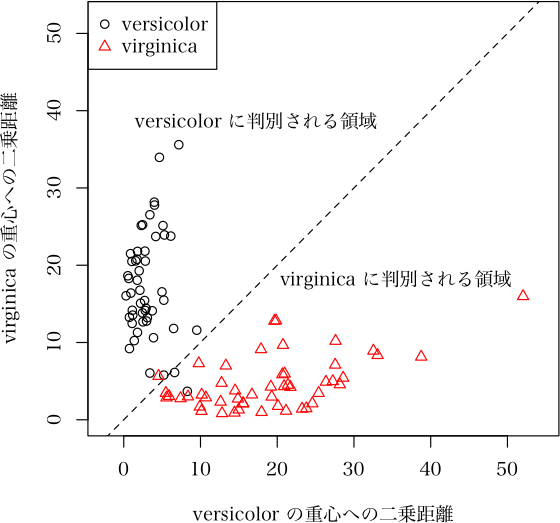
> plot(ans, which="scatter", xpos="topleft")
解説ページ
直前のページへ戻る E-mail to Shigenobu AOKI
