「統計学関連なんでもあり」の過去ログ--- 046

No.20528　ケンドールの一致係数の解釈　　【むむ】　2013/11/21(Thu) 12:50

ケンドールの一致係数について質問です。よろしくお願いします。

複数の対象の血管画像を3名の医師で5段階評価(0-4)し，その一致率の検定にケンドールの一致係数を使用しました。
一部，明らかにきれいな血管があり，ほとんど4, たまに3が混ざるデータが出来たのですが，一致係数が異様に低く出ます。
恐らく，計算上の誤謬？かと思いますが，この場合どう論文などに記載すればよろしいでしょうか。ご指導お願いします。

以下にデータの例とRGui を用いた評価をお示しします。

患者
A 4 4 4
B 3 4 4
C 4 3 3
D 4 4 4
E 4 4 4
F 4 4 4

Kendall W = 0.4444, chi sq. = 5.3333, df = 4, p-value = 0.2548

No.20534　Re: ケンドールの一致係数の解釈　　【青木繁伸】　2013/11/21(Thu) 15:22

「Rgui を用いた評価」とありますが，私の kendall.w を使ったのでしょうか？
必要ならば，手計算で，結果に間違いがないか確かめるとよいでしょう。
> d
  d1 d2 d3
A  4  4  4
B  3  4  4
C  4  3  3
D  4  4  4
E  4  4  4
F  4  4  4

> kendall.w(d)

	ケンドールの一致度係数

data:  d
Kendall W = 0.4667, chi sq. = 7.0000, df = 5, p-value = 0.2206
上の結果は，あなたの結果（下）と違うのですが，あなたは，どれかは分からないけど，「5 人分の結果しか使って（使えて）いない」のではないでしょうか？
> kendall.w(d[1:5,])

	ケンドールの一致度係数

data:  d[1:5, ]
Kendall W = 0.4444, chi sq. = 5.3333, df = 4, p-value = 0.2548
それはそれとして，この例のように，狭い範囲でごくわずか違う場合は大きな数値にはならないでしょう。広い範囲でわずかに違う場合は大きな数値になるでしょう。
> d2
  d1 d2 d3
A  4  4  4
B  3  4  4
C  4  3  3
D  4  4  4
E  2  1  2
F  1  1  1
> kendall.w(d2)

	ケンドールの一致度係数

data:  d2
Kendall W = 0.8768, chi sq. = 13.1522, df = 5, p-value = 0.02199
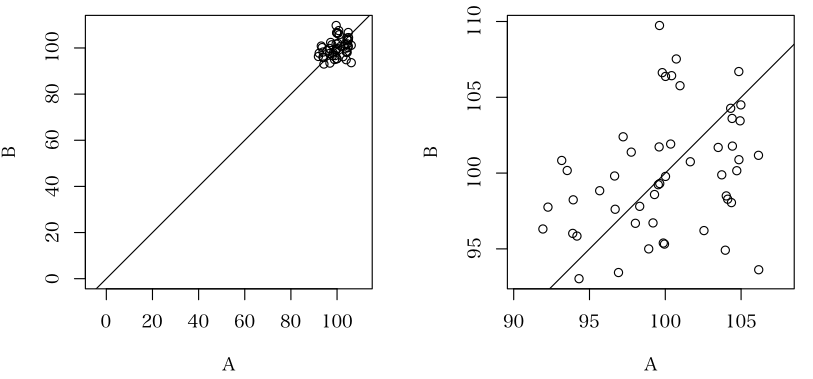
理由といわれても，自明ですが，二人の医師のデータで散布図を描けば明らかでしょう。

No.20539　Re: ケンドールの一致係数の解釈　　【むむ】　2013/11/21(Thu) 17:01

青木先生，素早いお返事ありがとうございます。

＞「Rgui を用いた評価」とありますが，私の kendall.w を使ったのでしょうか？
おっしゃる通り，先生のソースをお借りして計算しています。

＞あなたは，どれかは分からないけど，「5 人分の結果しか使って（使えて）いない」のではないでしょうか？
確認したところ，おっしゃる通り5人分のデータしか使用していませんでした。excel でデータ部分のみを選択したことで，1段目がデータとして利用されていなかった模様です。なお，やり直したところ，Kendall W = 0.4667, chi sq. = 7.0000, df = 5, p-value = 0.2206 と，先生のデータと同一のものがでました。大変失礼しました。

＞広い範囲でわずかに違う場合は大きな数値になるでしょう。
実は，掲示板に張るのが憚られて控えていたのですが，サンプル数は26 例です。ご迷惑を承知で以下にデータとその解析結果をお示しします。

d1 d2 d3
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 3 4
4 3 4
4 4 4
3 4 4
4 3 3
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4
4 4 4

Kendall W = 0.4398, chi sq. = 32.9832, df = 25, p-value = 0.1315

＞理由といわれても，自明ですが，二人の医師のデータで散布図を描けば明らかでしょう。
こういった明らかに一致率が高い場合は，ケンドールの一致係数での評価をせずに明らかであると断言してよろしいでしょうか。

No.20541　Re: ケンドールの一致係数の解釈　　【青木繁伸】　2013/11/21(Thu) 17:43

こういうのを，「一致率が高い」というかどうかの問題でしょう。
判定誤差（測定誤差）と変数の変域の比は，示された場合と，先頭の3例が (1,1,1)(2,2,2)，(3,3,3) である以外は示されたものと同じ場合でだいぶ違います。Kendall W は 0.4398 であったものが 0.8108になります。

このような状態は以下の図で説明できるでしょう。一定の状況下の検体を測定器 A, B で測定する。

一人の人はいう。
左図のように，原点を通る傾き 1 の直線の近辺（誤差範囲内）に分布しており，A, B の検査値は同等のものと見られる。

別の人がいう。
データは狭い範囲に限定されており，これを拡大すると右図のようになる。A, B の測定値間の相関はほとんど 0 だ。どちらもいい加減な数値を出しているに過ぎない。

No.20547　Re: ケンドールの一致係数の解釈　　【むむ】　2013/11/21(Thu) 19:33

迅速，丁寧かつわかりやすい解説，ありがとうございました。