「統計学関連なんでもあり」の過去ログ--- 046

No.20154　ロジスティック回帰分析　　【梶本】　2013/08/25(Sun) 20:09

よろしくお願いします。
現在，ある疾患の診断のための指標づくりに解析を行っています。
複数の項目をロジスティック回帰分析で解析し，疾患の診断のためのモデルを作ろうとしています。
解析により，
(定数)＋X1＋X2・・・X5
のような形で回帰式が得られました。
この回帰式からROC曲線を描こうとしていますが，疾患の有無を状態変数として設定し，上記の回帰式の値を各患者で算出したものを検定変数として設定した上でROC曲線を描いてカットオフ値を求めるという方法でよろしいでしょうか。
ロジスティック回帰分析での分類結果があまりよくないため，この手法で行えないかと考えています。
よろしくお願いいたします。

No.20156　Re: ロジスティック回帰分析　　【taipapa】　2013/08/26(Mon) 21:32

貴方が考えているのは以下の様なことでしょうか．．．
Rで，シミュレートしてみました．

> test.df <- data.frame(c(rep("A", 50), rep("B", 50)),round(c(rnorm(50, 60, 30),
+  rnorm(50, 60, 10)), 0), round(c(rnorm(50, 120, 30), rnorm(50, 130, 20)),0),
+  round(c(rnorm(50, 90, 20), rnorm(50, 95, 25))), round(c(rnorm(50, 20, 10),
+  rnorm(50, 20, 5)))) # 疾患タイプAとBそれぞれ50人で，年齢，LDL，血糖，BUNを測定（ほんの少しの差をつける）
> colnames(test.df) <- c("type", "age", "LDL", "glucose", "BUN")
> test.glm <- glm(type ~ age + LDL + glucose + BUN, family=binomial, data=test.df) # ロジスティック回帰を実行
> summary(test.glm)
………………………
Coefficients:
		Estimate	Std. Error	z value	Pr(>|z|)  
(Intercept)	-4.531526	2.184434	-2.074	0.0380 *
age		-0.009505	0.011225	-0.847	0.3971  
LDL		0.024929	0.010146	2.457	0.0140 *
glucose		0.018422	0.010991	1.676	0.0937 .
BUN		0.012410	0.029502	0.421	0.6740  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
…………
> library(epicalc)
> logistic.display(test.glm)

Logistic regression predicting type : B vs A 
 
                     crude OR(95%CI)        adj. OR(95%CI)         P(Wald's test) P(LR-test)
age (cont. var.)     0.989 (0.9697,1.0086)  0.9905 (0.969,1.0126)  0.397          0.388     
                                                                                            
LDL (cont. var.)     1.02 (1,1.04)          1.03 (1.01,1.05)       0.014          0.008     
                                                                                            
glucose (cont. var.) 1.01 (0.99,1.03)       1.02 (1,1.04)          0.094          0.086     
                                                                                            
BUN (cont. var.)     1 (0.95,1.05)          1.01 (0.96,1.07)       0.674          0.674     
……………….

# type Bになる確率は，prpbabilityB = 1/(1+exp(-Xbeta))なので，上記のsummary(test.glm)の表のEstimatedから計算する

> test.df2$Xb <- -0.009505*test.df$age + 0.024929*test.df$LDL + 0.018422*test.df$glucose + 0.01241*test.df$BUN
> test.df2$Xb2 <- test.df2$Xb - 4.531526
> test.df2$probabilityB <- 1/(1 + exp(-(test.df2$Xb2)))
# これで，Bになる確率がtest.df2のコラムprobabilityBに入る．
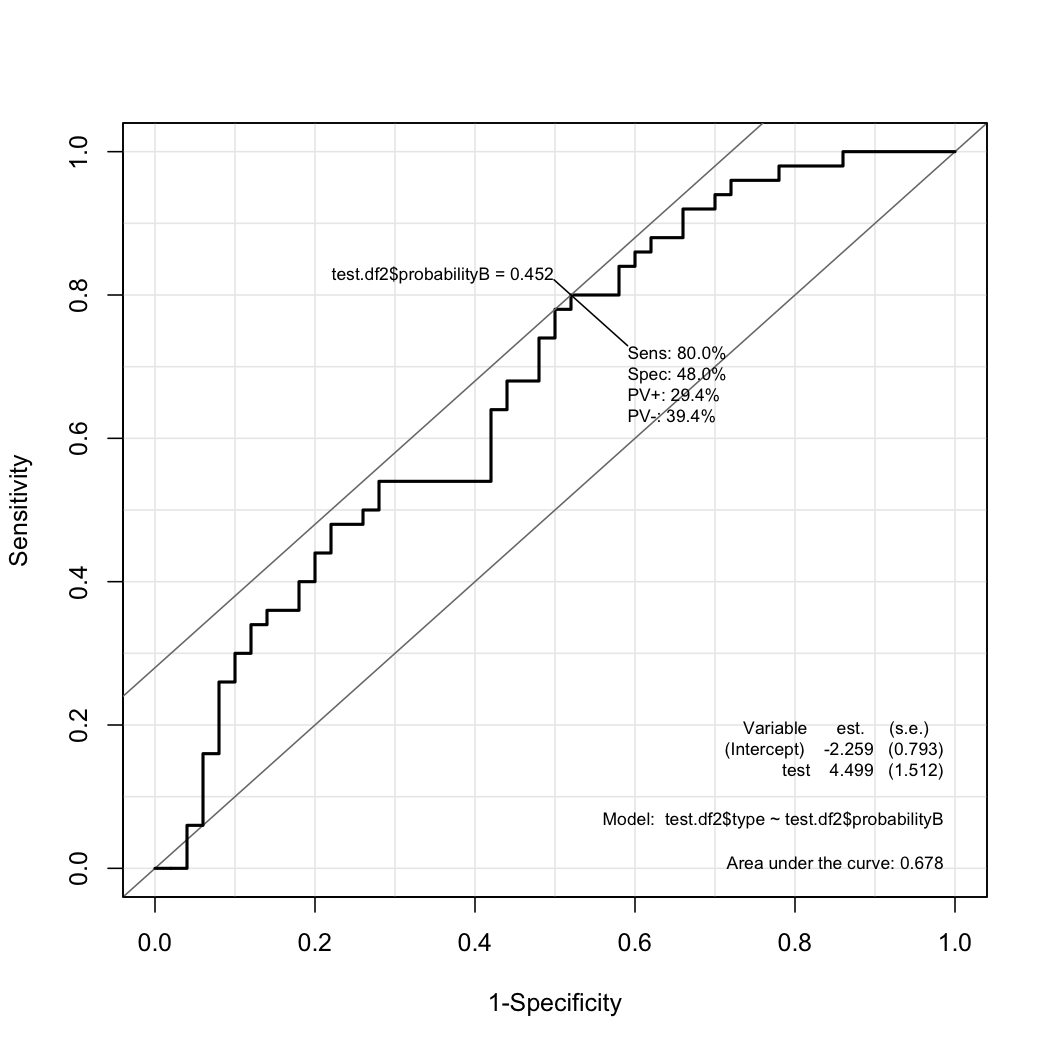
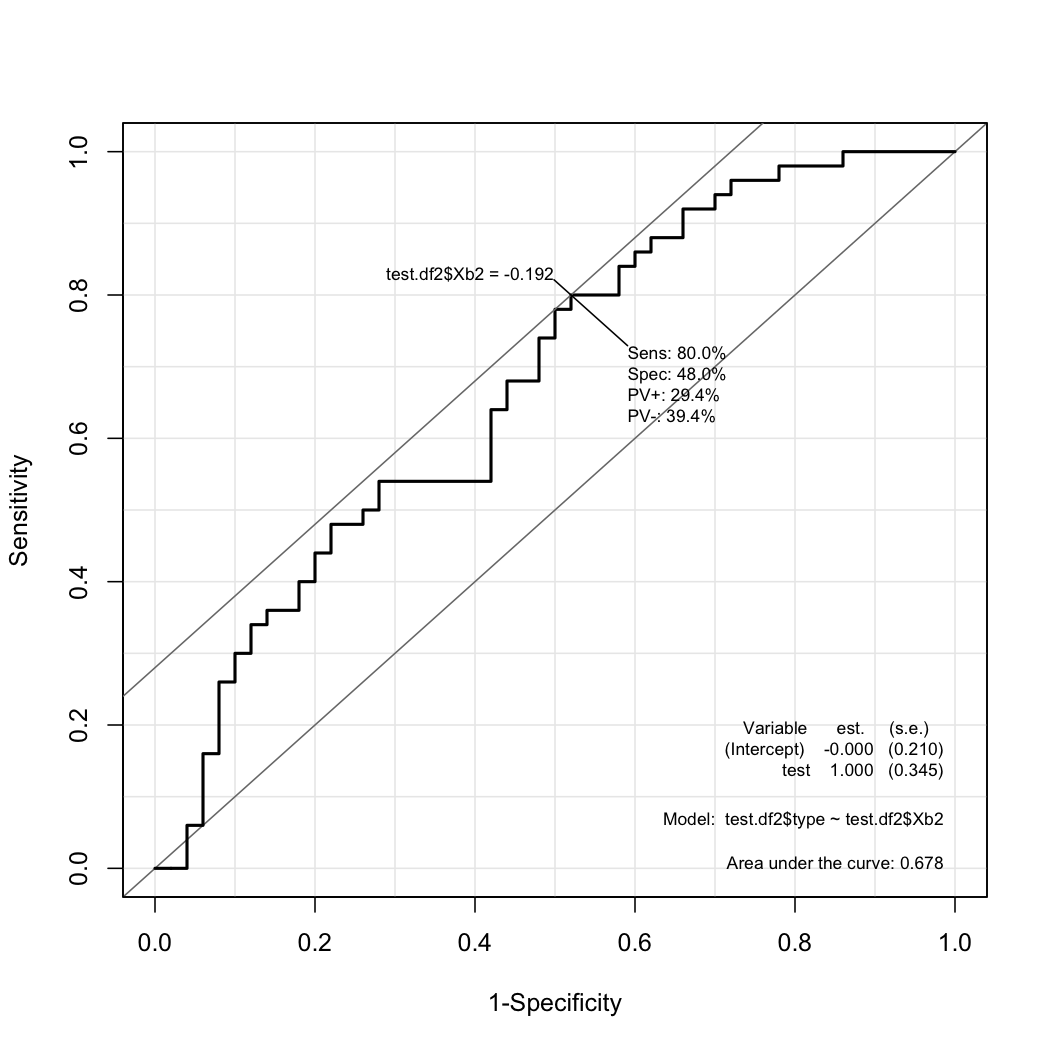
# この確率をもとに，ROC curveを書いてみる．
> library(Epi)
> ROC(test.df2$probabilityB, test.df2$type, plot="ROC")

この程度の差に医学的な意味があるかどうかは，また，別の問題でしょうが．．．
貴方のご希望にそっていますでしょうか？

No.20157　Re: ロジスティック回帰分析　　【梶本】　2013/08/27(Tue) 00:14

御返答ありがとうございます。
最初の私の書き方が不十分だったようです。
書いていただいたRでのコマンド例で考えますと

-0.009505*test.df$age + 0.024929*test.df$LDL + 0.018422*test.df$glucose + 0.01241*test.df$BUN- 4.531526

が回帰式になると思うのですが(この例でしたらtest.df2$Xb2)，この式に従って患者毎に「スコア」を算出します。
このスコアと疾患か否かについてROC曲線を描くことが統計学的に正しいのかがわからないために質問させていただきました。
つまりこのコマンド例に沿いますと

> ROC(test.df2$Xb2, test.df2$type, plot="ROC")

によって得られるROC曲線が統計学的に正しいか否かについてご教示お願いいたします。

No.20158　Re: ロジスティック回帰分析　　【taipapa】　2013/08/27(Tue) 00:48

probabilityBはXb2を変換しているだけなので，同じカーブになります（念の為に貼っておきます）．
「統計学的に正しいか？」とはどういう意味でしょうか？　Xb2とtypeのロジスティック回帰を行なうこと自体はまっとうな統計学的処理です．普通にやると思います．正しいかと言われれば正しいとしか言い様がありません．問題は，固有科学において，それにどのような意味があるかで，貴方のデータを知らない私としては，「それは貴方が考えるしかありません」と言わざるを得ないのですが．．．

No.20159　Re: ロジスティック回帰分析　　【梶本】　2013/08/27(Tue) 00:58

ありがとうございます。
taipapaさんと同じ曲線を描いていたんですね。
統計をまだ理解できていないようですので，明後日の方向で話してるかもしれません。
xb2とtypeのROC曲線を描くのが普通に行われているという理解でよろしいでしょうか?

No.20161　Re: ロジスティック回帰分析　　【青木繁伸】　2013/08/27(Tue) 18:56

何が議論になっているのかよくわからなかったので傍観しておりましたが

xb2 は linear.predictor 線形予測子です。それをロジスティック曲線に代入して得られるのが発生確率です。ちなみにそれぞれは glm の返すオブジェクトに含まれているので，再計算は不要です（fitted.values と predict 関数参照）。

発生確率は線形予測子の単調非減少関数なので，どちらを使っても ROC 曲線は同じになります。

そういう意味では「xb2とtypeのROC曲線を描くのが普通」というのはどうともいえないでしょう。

No.20162　Re: ロジスティック回帰分析　　【taipapa】　2013/08/27(Tue) 19:43

普段，あんまりglmを使わないので，オブジェクトまで見ておらず車輪の再発明もどきをやってしまいました．(^^;;;　ご指摘ありがとうございます．

発生確率を用いてROC curveを書くのが順当とは思いますが，スコア化するというなら，線形予測子（ここではXb2）ではなく，発生確率（probabilityB）の計算式自体を使って，患者さんごとに，「貴方がタイプBである確率は80％ですよ」とか予測できるようにした方が役に立つんじゃないかなぁと思います．ただ，それにはこんな程度のAUCではハズレすぎて無理がありますが．．．

なお，rms packageのlrmでは各予測因子と線形予測子と発生確率の関係がnanogoramで簡単に表示できて便利です．

＃青木先生，表の整形をやっていただき有難うございます．表がいつも乱れるのですが，スペースでもタブでもうまくいきません．ここでお聞きするべきではないかもしれませんが，どのように整形しているのか教えていただければ幸いです．

No.20163　Re: ロジスティック回帰分析　　【青木繁伸】　2013/08/27(Tue) 21:38

> どのように整形しているのか

記事の必要部分を＜pre＞～＜/pre＞で囲みます（ブラケットは小文字）。挿入位置に少しコツが必要なので，件の記事を「編集」で表示してみてください。

No.20164　Re: ロジスティック回帰分析　　【taipapa】　2013/08/27(Tue) 22:09

青木先生，有難うございます．今後は気をつけるようにいたします．