「統計学関連なんでもあり」の過去ログ--- 044

No.15570　散布図プロットの偏りの比較について。　　【H.M】　2011/10/27(Thu) 15:53

初めて質問させて頂きます。

医療系の学生です。
独立2群(A, Bそれぞれn=200)について，例えば，それぞれの個体内の部位の比を計算（胸囲／腹囲，大腿径／下腿径，上腕径／前腕径など）し，結果を散布図に示したとします。A,Bのデータを同じ散布図上に示した所，2群のプロット分布に視覚的に明らかなずれ（偏り）があるようにみられました。2群間のずれが統計学的に有意か（異なった分布であるのか）を統計学的に示したいと思うのですが，どのような方法が考えられますでしょうか？

統計初心者で恐縮なのですが，上記ご教授頂ければ幸いです。

No.15572　Re: 散布図プロットの偏りの比較について。　　【青木繁伸】　2011/10/27(Thu) 16:36

多変量に拡張された平均値の差の検定
http://aoki2.si.gunma-u.ac.jp/lecture/Wilks/wilks2.html
というのが，利用できるかも。
比を計算してというのが若干気になる。そんなことをしなくても，差があるものは差があるはずだから。恣意的に2変数の比をとるということが妥当かどうか?

No.15575　Re: 散布図プロットの偏りの比較について。　　【H.M】　2011/10/27(Thu) 17:32

青木先生　早速のご回答感謝申し上げます。

実際に研究で設定した変数は，個体ごとに各部位でのある指標を信号強度(intensity level)として測定したデータ（非正規分布）です。研究の性質上，信号測定の際に個体間で完全に同じ条件にならない（一個体内では同条件でスキャンが可能）可能性があり，各個体について部位間の信号強度を比で表し，個体間で比較するという方法を選択しました。例えが不適当で申し訳ございませんでした。
ご教授頂いた方法は，比で示したデータなどにも適応できますでしょうか？統計処理にはSPSSを用いているのですが，SPSSでの計算は可能でしょうか？

ご教授の程よろしくお願い申し上げます。

No.15581　Re: 散布図プロットの偏りの比較について。　　【青木繁伸】　2011/10/27(Thu) 21:16

> 教授頂いた方法は，比で示したデータなどにも適応できますでしょうか

厳密に言えば，検定対象になるデータは正規分布に従うべきもの（そんなに厳密な条件ではないが）。

比のデータは正規分布に従わない。よって，厳密に言えばそのデータには適用不可。
でもまあ，中心極限定理とか何とかありまして，まあ，どんな数値も単なるデータと見なせば適用して良いだろうというのが結論ではあります。
それより以前の問題として，比を取ることにどの程度の意味があるかが問題でしょう。

No.15588　Re: 散布図プロットの偏りの比較について。　　【H.M】　2011/10/28(Fri) 11:36

ご回答下さりありがとうございます。
先生ご指摘のように比を用いることのメリットを再検討し，生データと併せてノンパラメトリック法を検討致したいと思います。
このような場合，例えば，2群の散布図の中心（中央）座標を求めて，その偏りがどちらに偏っているかをみる方法などは考えられますでしょうか？（ものすごく抽象的な質問で申し訳ございません）。
また，たびたびの質問で恐れ入りますが，散布図における中心座標の求め方などがあれば，ご教示いただけましたら幸いです。

No.15590　Re: 散布図プロットの偏りの比較について。　　【青木繁伸】　2011/10/28(Fri) 17:22

> 散布図における中心座標の求め方

2変数の散布図ですね?
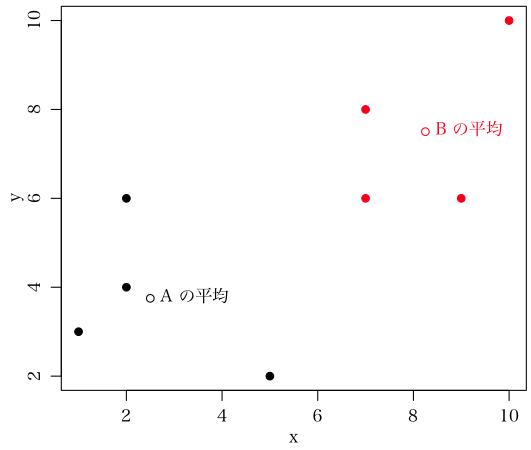
x と y の撒布図を描いたとき，あなたのいう中心座標は，各グループについて，x の中心（平均値や中央値）と y の中心を求めたものががそれですよ。
   x  y g
1  2  6 A
2  2  4 A
3  5  2 A
4  1  3 A
5  7  8 B
6 10 10 B
7  7  6 B
8  9  6 B
のように，A，B が 4 人ずつのとき，A においては x の平均値が 2.5, y の平均値が 3.75，B においては x の平均値が 8.25, y の平均値が 7.5 になるので，散布図での A の中心は (2.5, 3.75)， B の中心は (8.25, 7.5) となりますね?

それとも，何かほかのことでしょうか?

No.15593　Re: 散布図プロットの偏りの比較について。　　【H.M】　2011/10/28(Fri) 18:22

丁寧なご説明ありがとうございます。私の不勉強でした。
この場合は中心＝重心のように考えてもよいものなのでしょうか？
また，非正規性の生データについて，厳密には多変量分散分析という手法が厳密には適応できないとご指摘を頂きましたが，SPSSで一応，多変量検定を施行してみました。
共分散行列の等質性の検定の部分で，グループ間で等しいという帰無仮説が棄却されてしまったのですが，やはりこの手法が適当でないと考えた方がよろしいのでしょうか？
たびたびで恐縮ですが，ご教授頂ければ幸いです。

No.15594　Re: 散布図プロットの偏りの比較について。　　【青木繁伸】　2011/10/28(Fri) 18:50

平均値なら重心
中心という場合にはもう少し広い概念で，中央値でもよいでしょう。

> グループ間で等しいという帰無仮説が棄却されてしまったのですが，やはりこの手法が適当でないと考えた方がよろしいのでしょうか

「帰無仮説が棄却されてしまった」のは，正規分布でないことが原因ではない。
「共分散行列の等質性の検定」なのだから，各群のデータが正規分布に従っていても，等質でなければ帰無仮説は棄却されるでしょう?

No.15595　Re: 散布図プロットの偏りの比較について。　　【H.M】　2011/10/28(Fri) 20:34

青木先生，早速のご回答に感謝申し上げます。
基本事項があやふやで申し訳ございません。確かにご説明の通りでした。
分散分析では分散の均一性が前提条件とあり，統計量Fからの有意確率が0.000と有意になったのですが，気になりましたものでして。
多変量分散分析をやむなくノンパラメトリックで用いる場合，特に解釈を含めて注意すべき点などがございましたらお教え頂ければ幸いです。
ノートの説明で「2群間の平均ベクトルが異なる＝分布が異なる」ということの意味が具体的にどのようなことか少しイメージしずらいのですが，どのように理解したらよろしいでしょうか？

No.15596　Re: 散布図プロットの偏りの比較について。　　【青木繁伸】　2011/10/28(Fri) 22:29

> 「2群間の平均ベクトルが異なる＝分布が異なる」ということの意味が具体的にどのようなことか少しイメージしづらいのですが（「ず」じゃなくて「づ」）

申し訳ないですが，「散布図における中心座標の求め方などがあれば」などと同様，余りに初歩的な質問で，さすがにちょっと対応するのに難儀します。

一変量の場合（例えば身長のデータという場合），平均値が違えば分布は異なりますよね。
身長と体重の2変量の場合，身長と体重の平均値が違えば，先の No. 15590 に示すように，分布は違いますよね。分からないと言われても，それ以上どのように説明したらよいのかなあと困惑します。

No.15602　Re: 散布図プロットの偏りの比較について。　　【H.M】　2011/10/31(Mon) 17:41

青木先生ご回答ありがとうございます。統計の勉強を始めたばかりで，私の基礎が不十分で，断片的な知識なため基本的な質問ばかりになってしまい失礼を致しました。
実際には，例えば,
　　上腕,　　前腕
A1: 31,　　 26
A2:　 23,　　 15
A3: 21,　　　8
A4: 90, 50
A5: 99, 12
B1: 190, 140
B2: 160, 150
B3: 117, 72
B4: 188, 140
B5: 218, 102
ただしn=200，A1とB1,A2とB2・・は各々同一個体内での測定をあらわし，左と右のような同一個体での反復はなく，分布は上腕，前腕とも非正規であるdataが得られました。個体内で，レーザーBのほうがAよりも上腕あるいは前腕に信号が有意に偏るのような結論を出すために必要な統計手法を検討しています。そのため前にご教授頂きました（やむなくノンパラメトリックに用いた）多変量分散分析で，なおかつ対応のある場合のような手法がもしあれば適応できるかと考えております。見当違いであれば，どのような手法が考えられますでしょうか？
度々で恐れ入りますがご教授頂きたく宜しくお願い致します。

No.15603　Re: 散布図プロットの偏りの比較について。　　【青木繁伸】　2011/10/31(Mon) 18:20

> 個体内で，レーザーBのほうがAよりも上腕あるいは前腕に信号が有意に偏る

ということがどのようなことなのかよくわかりません。
どれとどれの比を取るの?それがどうなれば「偏る」ということになるの?
一番最初は A， B 群は独立二群とか書いていたけど。

No.15604　Re: 散布図プロットの偏りの比較について。　　【H.M】　2011/10/31(Mon) 18:35

早速のご回答感謝申し上げます。
私の表現が不適当でした。申し訳ございません。偏るというのは，「200 個の対応あるplotをレーザーAとBについて散布図上にoverlayしたときに，視覚的にレーザーBのplotがY軸方向（上腕）に偏ってみられたということです。この視覚的な偏りが統計学的に有意かを検定したいと考えております。
独立2群というのは私の見当違いでした。レーザーAとBというのは同一で波長の異なる成分をみているもので，独立ではなく「対応あり」にて考えることが適当かと考え直しました。
「比をとる」というのは例えば各部位についてB1／A1などの比をとってみてどうかと考えましたが，ご指摘頂きましたようにまずは生dataで何が言えるかを考え検討しております。

No.15608　Re: 散布図プロットの偏りの比較について。　　【青木繁伸】　2011/10/31(Mon) 20:32

15602 のデータ
  上腕A 前腕A 上腕B 前腕B
1    31    26   190   140
2    23    15   160   150
3    21     8   117    72
4    90    50   188   140
5    99    12   218   102
を図にしてみると以下のようになります。
これは一部分のデータでしょうが（実際のデータとは違うかも知れず），「レーザーBのplotがY軸方向（上腕）に偏ってみられた」というのは，矢印が水平線となす角度が45°より大きい（傾きが1より大きい）ということを言っているのでしょうか？
そうであれば，傾きはそれぞれ，
1.39473684210526
1.01481481481481
1.5 
1.08888888888889
1.32222222222222
なので，これが母平均1より大きいかどうかの片側検定をおこなえばよいのかもしれませんね。
http://aoki2.si.gunma-u.ac.jp/lecture/Average/Mean1.html
ここに書いてあるのは両側検定なので注意。
このデータについての片側検定の結果は以下の通り。
> t.test(x, mu=1, alt="greater")

	One Sample t-test

data:  x 
t = 2.8739, df = 4, p-value = 0.02264
alternative hypothesis: true mean is greater than 1 
95 percent confidence interval:
 1.068203      Inf 
sample estimates:
mean of x 
 1.264133 

No.15613　Re: 散布図プロットの偏りの比較について。　　【H.M】　2011/11/01(Tue) 18:40

青木先生　素早くかつ丁寧なご解説に感謝申し上げます。

私のdata(n=200)で，対応ある点についての傾きを求めた平均と傾き1を比較すると有意に1より大きいとなりました。ただ散布図で対応したベクトルをみると，中には傾きが1より大きく出るけれども，ベクトルとしては反対方向のものなどもみられました。傾きが1より大きいのみだと解釈の際には逆の要素（同じ傾きでベクトルが逆）も一緒に含むことになり，ベクトルの向きも考慮が必要なのか？と感じました（また理解が足らず，見当違いの内容でしたら申し訳ございません）。
結果については，レーザーAとBでは前腕（X軸方向）では統計的に有意な差はないが，上腕（Y軸方向）では有意にAよりBが強く励起されるといえるかが重要と考えました。ひとつ懸念されるAとBのレーザーgainの強さの差によるものであれば，このような偏りにはならないと思うのです。
以前にお教え頂きましたレーザーAとB全体の分布でおこなったWilksのΛによる平均ベクトルの比較では，SPSSで出力されるサブ解析でX軸成分（前腕）で有意差なし，Y軸成分（上腕）で有意差ありとなったのですが，これではplotの対応が考慮できていないと考えやはり不十分かと。。
教科書なども何冊か調べておりますが，適当な手法がはっきりせず，たびたびで，また知識も不十分で誠に恐縮ですが，解析手法についてのお考えをご教授いただけましたら幸いです。

No.15614　Re: 散布図プロットの偏りの比較について。　　【青木繁伸】　2011/11/01(Tue) 20:46

よほど，特殊な状況のようなので，固有科学の問題として，ご自分でよく考えてください。

No.15617　Re: 散布図プロットの偏りの比較について。　　【H.M】　2011/11/01(Tue) 21:33

青木先生お忙しい中，毎度丁寧にご回答いただきましてありがとうございました。

対応のある場合の多変量分散分析？なるものに相当する手法があるのかは解りませんが，そのようなものが該当するかもしれないと考えています。
200 枚の写真dataをそれぞれ見比べると結果は明らかなのですが，論文にそれを全て貼るわけにもいかず，，，intensityを数値化したもので違いを示そうと思ったのですが，適当な統計学的手法を選択して有意な差かを示すことの難しさがよく解りました。統計，数学素人の私ですがあきらめずに考えてみたいと思います。