No.14385　累積度数分布の差　　【yano】　2011/03/02(Wed) 17:05

ある薬剤について，副作用発現率と投与量（3群）の関係を知りたいと考えています。
複数の臨床試験の結果からデータを引用して統合解析を試みています。各臨床試験は3つの投与量のいずれかが用いられています。
臨床試験ごとに被験者数が異なるため，報告されている副作用発現率を単純に平均することは好ましくないと考えました。そこで，副作用発現率の累積度数分布曲線を描き，分布の差を見たところ，ある投与量群だけが明らかに異なった分布を示しています。
このような分布の差について検定するにはカイ二乗検定を行えば良いのでしょうか？

No.14390　Re: 累積度数分布の差　　【ひの】　2011/03/02(Wed) 22:47


分布の形の差の検定にはコルモゴロフ-スミルノフ検定が適当だと思います。
No.14393　Re: 累積度数分布の差　　【yano】　2011/03/03(Thu) 13:16

ひのさん，早速ご教示頂きありがとうございます。
コルモゴロフ-スミノルフ検定について勉強します。
代表値または分布の差の両方を検出する方法のようですね。

もう少し追加で質問させていただいて良いでしょうか？
1．この検定を3群に用いるには総当りで検定することになりますか
（A vs B, B vs C, A vs C)?

2．また，http://aoki2.si.gunma-u.ac.jp/R/ks2.html　によるとRを使って検定する際に，群間で要素数が異なるとダメ，なようですが，適当なカテゴリー化を行って要素数をそろえれば良いでしょうか？
No.14400　Re: 累積度数分布の差　　【青木繁伸】　2011/03/03(Thu) 16:38

> また，http://aoki2.si.gunma-u.ac.jp/R/ks2.html　によるとRを使って検定する際に，群間で要素数が異なるとダメ，なようですが，適当なカテゴリー化を行って要素数をそろえれば良いでしょうか？

この部分についてのみ。
使用例を見ればわかるように，ks2 は2つのベクトルを引数とし，そのベクトルは同じ長さでなくてはならないと言うこと。
「群間で要素数が異なるとダメ」というのが，何をどのように理解したものかよくわからないが，同じ長さのベクトルという意味ではそのとおり。両群のデータの大きさ（サンプルサイズが）同じでなければならないと言うことではない。

# 掲示された分布図ですが，横軸の意味がよくわからない。
No.14406　Re: 累積度数分布の差　　【yano】　2011/03/03(Thu) 17:53

青木先生，コメントを頂きありがとうございます。
ks2の引数が「同じ長さのベクトルでなければならない」ということが理解できました。

># 掲示された分布図ですが，横軸の意味がよくわからない。

様々な論文に報告された「薬剤Aの副作用発現率」，というつもりでしたが，いい加減な表現で作図してしまいました。大変失礼しました。
No.14407　Re: 累積度数分布の差　　【青木繁伸】　2011/03/03(Thu) 19:52

> 様々な論文に報告された「薬剤Aの副作用発現率」，というつもりでしたが，いい加減な表現で作図してしまいました

普通，横軸は時間とか，投与量とかになることが多いのではないかと思っていましたけど，投稿図は横軸は全ケースの累積副作用発現率ですか？横軸と縦軸に同じ要素が含まれているような違和感。
No.14408　Re: 累積度数分布の差　　【ひの】　2011/03/03(Thu) 20:03

＞1．この検定を3群に用いるには総当りで検定することになりますか
＞（A vs B, B vs C, A vs C)?

　1標本，2標本はありますが3標本以上というのは私は知りません（あるのかも知れない）。総当り法でやるなら有意水準の調整が必要ですね。
No.14410　Re: 累積度数分布の差　　【yano】　2011/03/04(Fri) 09:41

> 総当り法でやるなら有意水準の調整が必要ですね。

検定の多重性に注意しながら結果を解釈したいと思います。3標本以上の分布の差の検定があるのかどうかについては自信はありませんが調べてみたいと思います。ありがとうございました。

> 投稿図は横軸は全ケースの累積副作用発現率ですか？横軸と縦軸に同じ要素が含まれているような違和感。

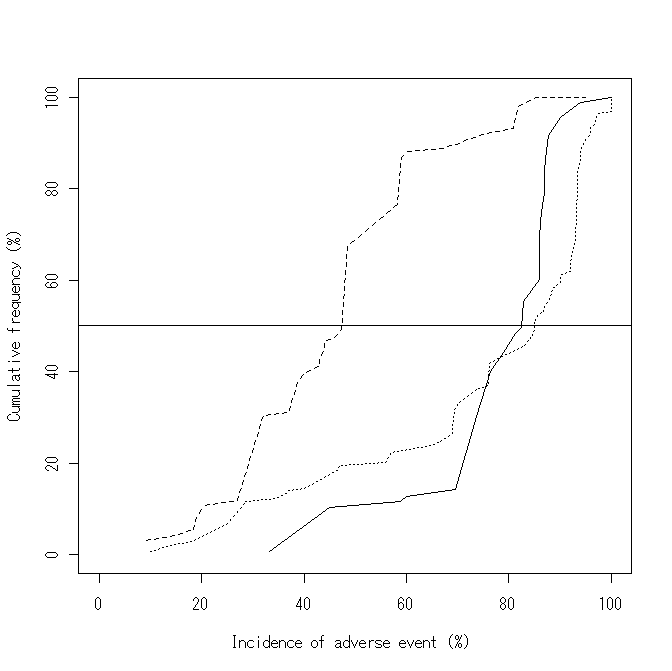
薬 剤Aを用いた臨床試験がたくさん報告されていて，使用されている投与量が3パターン(x,y,z)あります。臨床試験ごとにサンプルサイズ，報告されてい る副作用の発現率が異なります。この3つの投与量x,y,zで副作用発現率は異なるのか？ということを調べたいと思っています。
各投与量x(実線）,y（破線）,z（点線）ごとにサンプルサイズの合計を100%として，縦軸にサンプルサイズの累積度数をとり，横軸に副作用発現率をとってプロットしたものが掲示した分布図になります。おかしなことをやっていますか...?
No.14413　Re: 累積度数分布の差　　【青木繁伸】　2011/03/04(Fri) 11:47

> おかしなことをやっていますか...?

さあ。私には例えば図のAやBの位置がどういうことを表しているか良く理解できないだけです。

なお，"分布の違い"という場合は，http://aoki2.si.gunma-u.ac.jp/lecture/Average/kstest.html の例題に示すように，測定値を階級に区分して（二標本コルモゴロフ・スミルノフ検定では順序尺度でも良いのですが），各階級に幾つのデータが含まれるかを集計し，その累積相対度数に差があるかどうかを見るわけです。
あなたの図の元になっている度数分布表はどんな風になるんでしょうか?その度数分布表で階級分けされるのは副作用発現率ですよね。副作用発現率が 0.5〜0.6 の階級に何人属するなどという集計表になるんですか?

No.14414　Re: 累積度数分布の差　　【青木繁伸】　2011/03/04(Fri) 12:45

色々考えて，以下のようなことなのかなあと思いました。

まず，対象施設はたくさんある。そして，各施設において治療を受けた対象者もたくさんいる（なんてったって，副作用発現率が十分な精度をもって計算されるのだから）。データは以下のようになる。
   施設 患者数 投与量 副作用発現数 副作用発現率
1     A    359    med          151    0.4206128
2     B    809    med          120    0.1483313
3     C    467     lo          151    0.3233405
4     D    892     lo          163    0.1827354
5     E    943     hi          142    0.1505832
          略
xx   ZY    675     lo          170    0.2518519
yy   ZZ    720    med          248    0.3444444
そしてこれを集計したクロス集計表が
                       副作用発現率
      (0.1,0.15] (0.15,0.2] (0.2,0.25] (0.25,0.3] (0.3,0.35] (0.35,0.4]
  lo         集計表の各セルには，各施設の副作用発現率に対応する
  med        患者数（副作用発現数?それとも施設数?）が入る
  hi         どれを使うかによってそれこそケース数のアンバランスが影響する
実際は副作用発現率はもっと細かく階級分けされるのだろうけど。

でも，このデータをこんな風にして分析する意味はどこにあるのだろうか?しかも，各施設に属する治療例の副作用データを施設単位の副作用率にまとめてしまい，さらにそれを階級にまとめてしまう。データの持つ情報を捨てまくっている。

「臨 床試験ごとに被験者数が異なるため，報告されている副作用発現率を単純に平均することは好ましくない」のは事実だろうが，データの持つ情報を最大限利用す るのは，各治療例ごとの「副作用あり/なし」でしょう。それを従属変数として，「施設」，「投与量」およびその他の情報を表す変数も含めてロジスティック 回帰分析をするのが妥当なのでは?
No.14420　Re: 累積度数分布の差　　【yano】　2011/03/04(Fri) 18:11

> 副作用発現率が 0.5〜0.6 の階級に何人属するなどという集計表になるんですか?
> まず，対象施設はたくさんある。そして，・・・・（なんてったって，副作用発現率が十分な精度をもって計算されるのだから）。

ク ロス集計表のイメージは青木先生が書かれたとおりです。各セルに入るのは施設ごとの副作用発現率ではなく，臨床試験ごとの（論文ごとの）副作用発現率で す。各臨床試験の規模はまちまち（数十〜数百）なので，精度の低いものも含まれます。それらをひっくるめて，全体として投与量と副作用発現率の関係をつか みたくてあれこれ検討していました。

ご指摘の通り，「副作用のあり/なし」には様々な変数が関与します。中でも，人種差に注目しているの ですが，「アジア人対象の臨床試験では投与量が少ないのに副作用発現率が高い」傾向があり，「投与量が少ない臨床試験は大半がアジア人の臨床試験である」 ことから，投与量ごとの副作用発現率の分布を比較してみようと思いました。

> 各治療例ごとの「副作用あり/なし」でしょう。それを従属変数として，「施設」，「投与量」およびその他の情報を表す変数も含めてロジスティック回帰分析をするのが妥当なのでは?

論文に発表されたデータをもとに検討しているので個人個人の「副作用あり/なし」は把握できませんでした。今後，既知の変動因子や人種差などを変数に，ロジスティック回帰分析を行っていく予定です。

いろいろと示唆に富むご指摘をありがとうございます。
No.14422　Re: 累積度数分布の差　　【青木繁伸】　2011/03/04(Fri) 18:29

> 各セルに入るのは施設ごとの副作用発現率ではなく，臨床試験ごとの（論文ごとの）副作用発現率です。

この時点ですでにおかしいです。
二標本コルモゴロフ・スミルノフ検定の元になるのは，度数分布表ですから，セルの中に計数データでないものは入りません。

デー タがおかしかった理由は，「論文に発表されたデータをもとに検討しているので個人個人の「副作用あり/なし」は把握できませんでした」につきるわけです。 原データなくして二標本コルモゴロフ・スミルノフ検定はできませんよ（原データでなくても，全例数と各群の各カテゴリーの頻度 f(i) がわかっていれば可）。
No.14424　Re: 累積度数分布の差　　【青木繁伸】　2011/03/04(Fri) 18:57

結局，問題点は

> 臨床試験ごとに被験者数が異なるため，報告されている副作用発現率を単純に平均することは好ましくないと考えました。

ということだけですね。

被験者数が異なるので単純に平均することができないのですから，重み付きの平均を求めれば良いだけです。施設ごとの被験者数と副作用発現率があるのでしょうから，それぞれを ni, pi とすれば，全体の重み付き平均値（重み付きの副作用発現率）は，sum(ni * pi) /sum(ni) ですよ。これがなぜ，副作用発現率の重みつき平均になっているかは，式をちょっと変形すれば理解できるでしょう。それに，この式は，まとめるべき集団につ いて，合計した副作用発現数を合計した患者数で割るという，当たり前の計算式になっているのです。これがそれぞれ投与量の異なる3つの群について計算され る。クロス集計表で表すとすれば，ni1，pi1などの2番目の添え字は用量群を識別するためとして，
　　　　　患者数　　副作用発現数
低用量　　sum(ni1)　　sum(ni1 * pi1)
中用量    sum(ni2)　　sum(ni2 * pi2)
高用量    sum(ni3)　　sum(ni3 * pi3)
この集計表は患者数が合計欄になりますけど，3×2の分割表（カイ二乗検定），同じことですが，3群の比率の差の検定ということです。3群全体として比率に差があるか見た後，どの二群の間で差があるか知りたければ多重比較もできると言うことです。
No.14427　Re: 累積度数分布の差　　【yano】　2011/03/05(Sat) 10:45

青木先生，ご丁寧に解説いただきましてありがとうございます。
「副作用発現率」にこだわりすぎて，それが「副作用発現数/患者数」であるという単純なところからどんどん離れて袋小路にはまっていたわけですね。
重み付き平均を求める（＝各群の全副作用発現数/各群の全患者数），2x3の分割表で比率の差の検定を行う，ということですっきりしました。
大変なお手数をおかけいたしました。

● 「統計学関連なんでもあり」の過去ログ--- 044 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る