「統計学関連なんでもあり」の過去ログ--- 044

No.14186　判別分析での各群への所属確率　　【ai】　2011/01/22(Sat) 01:13

マハラノビスの平方距離に基づき，ある1つの検査値である病気の有無を判別したいとします。仮に「病気でない群」の検査値の平均値が20，分散が4，「病気群」の検査値の平均値が30，分散が4とします。

検査値が変化した場合に「病気群」に属する確率がどう変化するのかを把握するために，グラフの横軸に検査値，縦軸に「病気でない群」に属する確率と「病気群」に属する確率を描きました。すると検査値が30をピークとして，その後は検査値が大きくなるほど「病気群」に属する確率は減ってしまいます。また検査値が14以下や36以上の範囲では「病気でない群」と「病気群」の所属確率はどちらも0%になってしまいます。これはどう考えたらよろしいのでしょうか。

以下の過去ログにあるように，「病気群」と「病気でない群」の構成比を各群に属する確率と置き換えるべきでしょうか。

http://aoki2.si.gunma-u.ac.jp/lecture/mb-arc/arc036/08977.html

ご指導よろしくお願い致します。

No.14191　Re: 判別分析での各群への所属確率　　【青木繁伸】　2011/01/22(Sat) 21:21

> また検査値が14以下や36以上の範囲では「病気でない群」と「病気群」の所属確率はどちらも0%になってしまいます。これはどう考えたらよろしいのでしょうか。

　1 変量なのですから，マハラノビスの汎距離など考える必要はなく，単なる数直線上の，ユークリッド距離を考えれば良いだけです。
　そのような領域にデータが存在する確率は0に近いので，もしそのようなデータがあっても，それはどちらの母集団にも含まれないと考えるのが普通でしょう。悩む必要はないと思いますけど？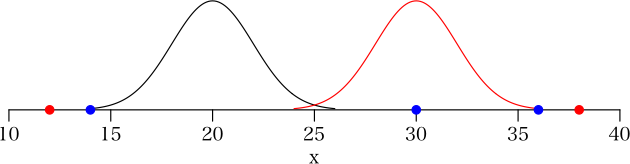

No.14193　Re: 判別分析での各群への所属確率　　【ai】　2011/01/22(Sat) 23:36

青木先生，早速ご返信頂きありがとうございました。

>1 変量なのですから，マハラノビスの汎距離など考える必要はなく，単なる数直線上の，ユークリッド距離を考えれば良いだけです。

実際は2群の分散が異なりました。申し訳ありません。「病気でない群」の検査値の平均値が20，分散が8，「病気群」の検査値の平均値が30，分散が4の場合はマハラノビスの汎距離を使うということでよろしいでしょうか。

>そのような領域にデータが存在する確率は0に近いので，もしそのようなデータがあっても，それはどちらの母集団にも含まれないと考えるのが普通でしょう。

仰るようにそのような領域にデータが発生する確率は0に近いと思いますが，しかしもし発生した場合にはその人は必ず「病気」か「病気でない」のどちらかの状態だと思うので，「どちらの母集団にも含まれない」ということはありえないと思うのですが。。。

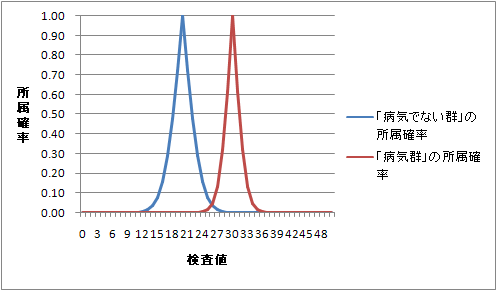
以下のように検査値と所属確率の関係を示すグラフを作成したいと思っているのですが，以下の2点がどうしても腑に落ちません。
1)上記にも書きましたように，状態としては「病気」か「病気でない」のどちらかしかありえないのに，各群の所属確率の合計が100%にならない。
2)実際の現場では検査値が高いほど「病気群」である可能性は高いのに，以下のグラフでは検査値が30以上では検査値が高いほど「病気群」の所属確率は低くなってしまう。

何か根本的に勘違いしておりましたら申し訳ありません。
お手数をお掛け致しますが，よろしくお願い致します。

No.14195　Re: 判別分析での各群への所属確率　　【青木繁伸】　2011/01/23(Sun) 09:49

> もし発生した場合にはその人は必ず「病気」か「病気でない」のどちらかの状態だと思うので，「どちらの母集団にも含まれない」ということはありえないと思うのですが。。

その病気ではないが別の病気である（健康でもない）ということもあるでしょう

それと，示される確率は，「そのデータがある母集団に含まれるとしたときそのデータよりも重心から離れたデータが存在する確率」Pr{χ二乗>カイ二乗値の標本値} ですよ。足しても1にならないのは当然です。
足して1になるというような確率を求めるには，ベイズ確率を求めて，分母に各群のベイズ確率の和，分子にそれぞれの群の確率というようにすればよいでしょう。正準判別の場合に計算例があります。http://aoki2.si.gunma-u.ac.jp/R/candis.html

No.14216　Re: 判別分析での各群への所属確率　　【ai】　2011/01/25(Tue) 01:52

青木先生，ご回答いただきありがとうございました。

>それと，示される確率は，「そのデータがある母集団に含まれるとしたときそのデータよりも重心から離れたデータが存在する確率」Pr{χ二乗>カイ二乗値の標本値} ですよ。足しても1にならないのは当然です。

やはり勘違いしておりました。ご指導ありがとうございます。今回求めたいのは足して1になる確率でした。

>足して1になるというような確率を求めるには，ベイズ確率を求めて，分母に各群のベイズ確率の和，分子にそれぞれの群の確率というようにすればよいでしょう。正準判別の場合に計算例があります。http://aoki2.si.gunma-u.ac.jp/R/candis.html

初歩的な質問で大変恐縮なのですが，教えて頂いた正準判別の計算式でベイズ確率が求められるのはどうしてでしょうか。また今回，1変量で2群を判別したいのですが，正準判別分析とマハラノビスの汎距離による判別分析で，ベイズ確率の算出方法は異なりますでしょうか。

お手数をお掛け致しますがよろしくお願い致します。

No.14217　Re: 判別分析での各群への所属確率　　【青木繁伸】　2011/01/25(Tue) 06:59

> 1変量で2群を判別したいのですが，正準判別分析とマハラノビスの汎距離による判別分析で，ベイズ確率の算出方法は異なりますでしょうか。

同じと思いますが，一変量なので，正準判別だの線形判別だのいわずに，OCR 曲線でも描く方が分かりやすいのではないでしょうかね。

> 実際は2群の分散が異なりました。申し訳ありません。

では，等分散を仮定する線形判別分析（や，正準判別分析）はできませんね。二次の判別分析をやってみるとよいでしょうか。

> 教えて頂いた正準判別の計算式でベイズ確率が求められるのはどうしてでしょうか

そのようなものですからです。丁寧な説明を求めるならば，しかるべき論文・教科書を見てください。

No.14218　Re: 判別分析での各群への所属確率　　【ai】　2011/01/25(Tue) 12:26

青木先生，ご回答ありがとうございます。

>では，等分散を仮定する線形判別分析（や，正準判別分析）はできませんね。二次の判別分析をやってみるとよいでしょうか。

はい，マハラノビスの汎距離による判別分析を行なってみたいと思います。

> そのようなものですからです。丁寧な説明を求めるならば，しかるべき論文・教科書を見てください。

多変量解析の教科書を何冊か調べてみたのですが，該当箇所を見つけることができませんでした。判別分析におけるベイズ確率の利用について記載した教科書や論文にはどのようなものがあるか，ご教授頂けませんでしょうか。

よろしくお願い致します。

No.14219　Re: 判別分析での各群への所属確率　　【青木繁伸】　2011/01/25(Tue) 12:49

丁寧な説明というわけでもないし，古い本ですが，
三宅一郎他「SPSS統計パッケージ II 解析編」東洋経済
の88-89ページに，以下のように書かれています（少し編集）。これだけあればプログラムは書けるでしょう。（http://aoki2.si.gunma-u.ac.jp/R/candis.html のプログラム参照）
図はクリックで原寸表示

No.14223　Re: 判別分析での各群への所属確率　　【ai】　2011/01/25(Tue) 22:18

青木先生，教科書の原文までお示し頂き本当にありがとうございました。
お陰様で進むべき道が分かって参りました。

度々で恐縮ですが，お示し頂いた内容について質問させて頂けますでしょうか。

1)文章中に「各グループの分散・共分散行列が同等であることを仮定すれば」とありますが，今回の私のデータは2群の分散が異なるのですが大丈夫でしょうか。

2) 事前確率についてですが，現在分析しているデータにおける事前確率（病気群のデータ数/全データ数）ではなく，現実場面における事前確率（病気の発症率）を用いた方が適切であるように思えるのですが，それでよろしいでしょうか。現在分析しているデータでは，「病気群」と「病気でない群」のデータ数がほぼ同じで，現実場面における割合とは異なります。

3)文章中では「判別得点y」という用語が使用されていますが，測定された検査値（検査値により病気の有無を判別したいと思っております）をそのまま代入してしまってよろしいのでしょうか。

お手数をお掛け致しますがよろしくお願い致します。