No.14045 Re: 原点を通る直線による回帰分析における,変数の対対称性 【青木繁伸】 2010/12/28(Tue) 11:44
R でちょっと書いて見た。解析的な解を求めるのは面倒なので,optimize 関数でお茶を濁す。
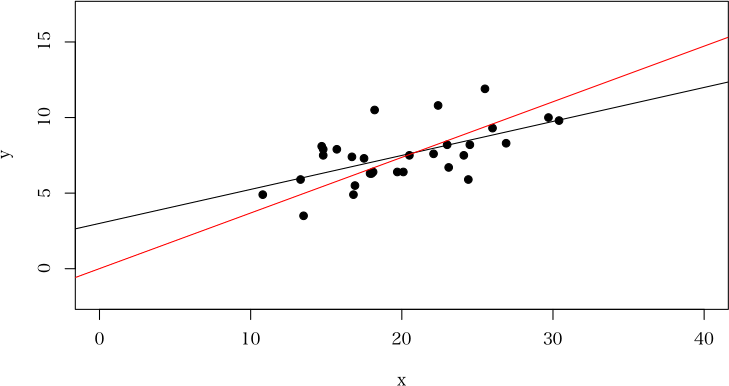
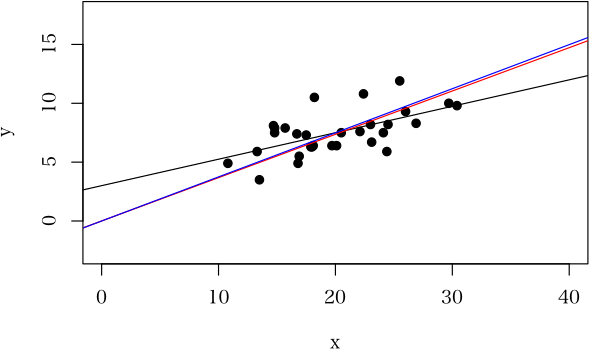
赤の直線が,原点を通り,「点と直線の距離」の二乗和が最小になる解。
reg <- function(x, y, rng)
{
func <- function(a)
{
x2 <- (x+a*y)/(a^2+1)
y2 <- a*x2
retv <- sum((x-x2)^2+(y-y2)^2)
return(retv)
}
ans <- optimize(func, rng)
return(ans)
}
x <- c(13.3, 20.5, 18, 17.5, 14.8, 18.1, 23, 14.7, 10.8, 20.1, 26,
13.5, 15.7, 14.8, 18.2, 30.4, 29.7, 26.9, 16.8, 24.5, 16.7, 24.1,
24.4, 16.9, 25.5, 19.7, 23.1, 17.9, 22.4, 22.1)
y <- c(5.9, 7.5, 6.3, 7.3, 7.5, 6.4, 8.2, 8.1, 4.9, 6.4, 9.3, 3.5,
7.9, 7.9, 10.5, 9.8, 10, 8.3, 4.9, 8.2, 7.4, 7.5, 5.9, 5.5, 11.9,
6.4, 6.7, 6.3, 10.8, 7.6)
plot(x, y, pch=19, xlim=c(0, 40), ylim=c(0, 15), asp=1)
abline(lm(y ~ x))
slope <- reg(x, y, c(0.01, 100))$minimum
abline(0, slope, col="red")