No.13634 Re: 3次元データの分布パラメータの推定について 【青木繁伸】 2010/10/19(Tue) 11:46
どこかで見たような質問だなあと思ったら,RjpWiki の中級者Q&A にあった,リンゴのお尻の窪みに曲面をフィットさせるというものでしたね。それが二次元正規分布と関係ないのではないかという指摘に,確率分布には意味が ないとのことでしたね。しかし,その曲面が数式で表せるかどうかは,その曲面の生成機序が大きく関わっていると思いますけどね。
曲面フィッティングは曲線フィッティングとなんら変わるところはありません。一変数なら曲線,二変数なら曲面,3変数以上なら超曲面。R なら optim でできるでしょう。
> # テストデータ生成(二次元正規分布,ただし,二変数は無相関とする)
> set.seed(123)
> func <- function(x, y) exp((-(x-mu.x)^2/sigma.x^2-(y-mu.y)^2/sigma.y^2+
+ 2*rho.xy*(x-mu.x)*(y-mu.y)/sigma.x/sigma.y)/
+ (2*(1-rho.xy^2)))/(2*pi*sigma.x*sigma.y*sqrt(1-rho.xy^2))
>
> size <- 20 # x, y 軸それぞれの座標点の数
> r.x <- 8
> x <- seq(mu.x-r.x, mu.x+r.x, length=size)
> r.y <- 10
> y <- seq(mu.y-r.y, mu.y+r.y, length=size)
> z <- matrix(0, size, size)
> mu.x <- 20 # mu.x, sigma.x, mu.y, sigma.y
> sigma.x <- 3
> mu.y <- 50
> sigma.y <- 5
> rho.xy <- 0.0
> for (j in 1:size) {
+ for (i in 1:size) {
+ z[i, j] <- func(x[i], y[j])
+ }
+ }
> xyz <- cbind(expand.grid(x, y), jitter(c(z), amount=0)) # z には誤差を加える
> xyz <- data.frame(xyz)
> colnames(xyz) <- letters[24:26]
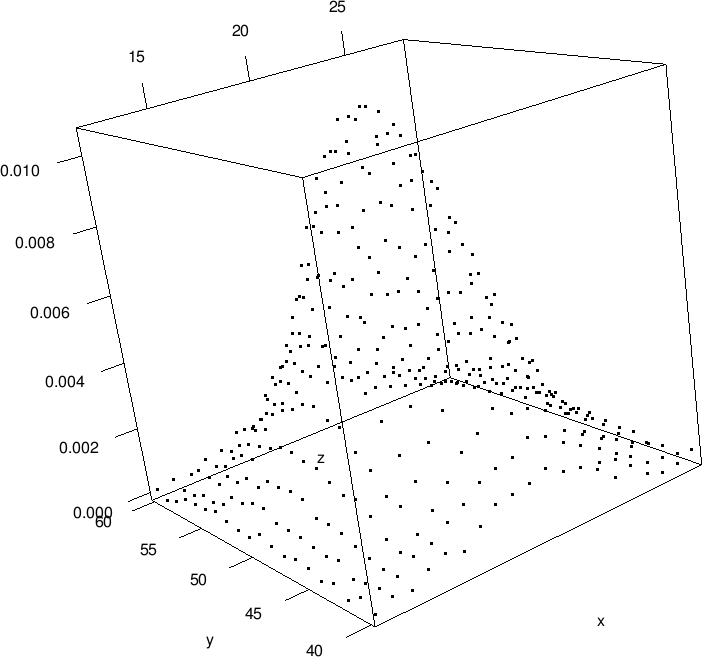
> plot3d(xyz) # 添付図のようなデータになる
> write.table(xyz, "xyz") # データを書き出しておく
> head(xyz)
x y z
1 12.00000 40 -4.741088e-05
2 12.84211 40 2.033789e-04
3 13.68421 40 1.186800e-04
4 14.52632 40 4.312480e-04
5 15.36842 40 6.194453e-04
6 16.21053 40 4.574655e-04
> # あてはめを行う
> fn <- function(par) { # mu.x, sigma.x, mu.y, sigma.y を推定
+ mu.x <- par[1]
+ sigma.x <- par[2]
+ mu.y <- par[3]
+ sigma.y <- par[4]
+ rho.xy <- 0.0
+ ss <- 0 # 残差平方和
+ for (i in 1:nrow(xyz)) {
+ x <- xyz[i, 1]
+ y <- xyz[i, 2]
+ hat.z <- exp((-(x-mu.x)^2/sigma.x^2-(y-mu.y)^2/sigma.y^2+
+ 2*rho.xy*(x-mu.x)*(y-mu.y)/sigma.x/sigma.y)/(2*(1-rho.xy^2)))/
+ (2*pi*sigma.x*sigma.y*sqrt(1-rho.xy^2))
+ ss <- ss+(xyz[i, 3]-hat.z)^2
+ }
+ return(ss)
+ }
> xyz <- read.table("xyz", header=TRUE)
> par <- c(21, 2, 48, 4) # mu.x, sigma.x, mu.y, sigma.y の初期値
> optim(par, fn)
$par
[1] 20.004417 3.002613 49.981011 5.002016 # 推定結果
$value
[1] 5.509302e-06 # 残差平方和
$counts
function gradient
189 NA
$convergence
[1] 0 # 収束している
$message
NULL