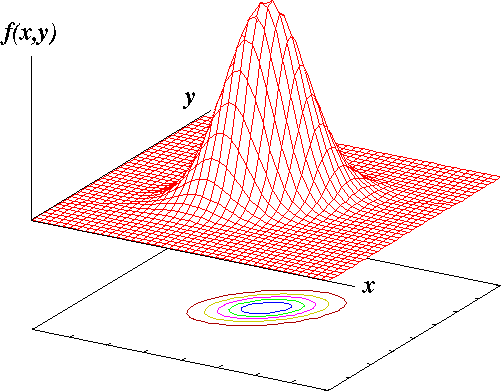
 図 1.二次元正規分布の概形 |
|---|
二次元正規分布の概形は図 1 に示すような山形である。
 図 1.二次元正規分布の概形 |
|---|
$x$,$y$ の分布の母分散を $\sigma_{x}^2$,$\sigma_{y}^2$ とする。母共分散 を $\sigma_{xy}$ とする。
このとき,二次元正規分布の密度関数は次式で表される。
\[ f(x, y) = \frac{1}{2\ \pi \ \sigma_x \ \sigma_y\sqrt{1-\rho_{xy}^2}}\ \exp \left [ - \frac{1}{2(1-\rho_{xy}^2)} \left \{ \frac{(x-\mu_x)^2}{\sigma_x^2} + \frac{(y-\mu_y)^2}{\sigma_y^2} - \frac{2\ \rho_{xy}\ (x-\mu_x)\ (y-\mu_y)}{\sigma_x\ \sigma_y} \right \} \right ] \] 上式の指数部を $-c^2\ /\ 2$ とおく,すなわち, \[ \frac{1}{2(1-\rho_{xy}^2)} \left \{ \frac{(x-\mu_x)^2}{\sigma_x^2} + \frac{(y-\mu_y)^2}{\sigma_y^2} - \frac{2\ \rho_{xy}\ (x-\mu_x)\ (y-\mu_y)}{\sigma_x\ \sigma_y} \right \} = \frac{c^2}{2} \] とすると,これは相似な楕円を表すことになる。さらに,楕円上の点 $(x, y)$ は全て, \[ f(x, y) = \frac{1}{2\ \pi \ \sigma_x \ \sigma_y\sqrt{1-\rho_{xy}^2}}\ e^{-c^2/\ 2} \] という確率を持つ。このため,これを 等確率楕円 または 集中楕円 と呼ぶ(図 1 の下の部分にある同心楕円)。
等確率楕円の内側の点の全確率は $\displaystyle 1 - e^{\displaystyle - c^2\ /\ 2}$ になることが示される。
演習問題:
応用問題: