No.08650 Mantel統計量とCochran-Armitage(CA)統計量の関係 【尾島俊之】 2008/12/16(Tue) 09:37
過去ログで下記の記載があります。
http://aoki2.si.gunma-u.ac.jp/lecture/mb-arc/arc011/003.html
> Re^3: CA検定 ??? 2000/11/05 (日) 12:44
> (Mantel統計量)=(CA統計量)*(N/(N-1))
一方で,SPSSのサポートページに
> CA test statisitic = LLA * (N/(N-1))
> LLA: Linear-by-Linear Association
> LLA は Mantel-Haenszel test for trend と同じ
との記載があります。
両者の記述は,N/N-1 の分子分母が逆になっていますが,どちらが正しいでしょうか。
No.08789 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【尾島俊之】 2008/12/28(Sun) 22:13
上記で質問しました件について,関連文献を探してみました。
Cochran-Armitage test for trend
Wikipedia: http://en.wikipedia.org/wiki/Cochran-Armitage_Test_for_Trend
Agresti, Alan (2002). Categorical Data Analysis (Second Edition). Wiley. pp181-182
Mantel test (Mantel's trend test)
Wikipedia: http://en.wikipedia.org/wiki/Mantel_test
Sokal, R. R., & Rohlf, F. J. (1995). Biometry, 3rd edn. New York: Freeman. pp 813-819
Mantel, N. (1967). The detection of disease clustering and a generalized regression approach. Cancer Research, 27, 209-220. http://cancerres.aacrjournals.org/contents-by-date.0.shtml
しかしながら,素人目には全くことなる雰囲気の式が並んでいて,全く分かりません。
どちらに,N/(N-1) を掛ければ他方になるか,どなたかわかりましたら大変助かります。
No.08790 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2008/12/28(Sun) 22:26
> 一方で,SPSSのサポートページに
URL を示しておくと,何らかの参考になるかも知れないと思いますけど?
もっとも,
Mantel統計量 と CA統計量 が,計算されていれば,
(Mantel統計量)=(CA統計量)*(N/(N-1)) かどうかは,すぐに確かめられるのでは?
それぞれの統計量の確かな定義式はどこかにないのでしょうか?
Mantel統計量といわれても,マンテルが関与している統計量って,1つじゃないような。
また,CA統計量についてもしかり?厳密な議論をしたいなら,まず定義をはっきり。(定義をはっきりさせられないからこその質問ではあるのでしょうけど。だったら,なおさら議論は難しいでしょう)
あるいは,SPSS では両方とも計算されるのでしょうか(これも,そうじゃないから,質問が出るんでしょうけどね。)
それにまあ,N が大きければ,両者は殆ど同じと言っているようなものなので,どうでもいいような気もしますけど。
No.08792 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2008/12/29(Mon) 00:11
よく分かっている人がちゃんとやってみるのがよいとは思うのですけど,
CA検定とMantel-Haenszel検定の関係がはっきりしないものの,
Chi-Square With Ordinal Data
http://www.uvm.edu/~dhowell/StatPages/More_Stuff/OrdinalChisq/OrdinalChiSq.html
の例を見ると,
Linear 1 5.757
というところと,Chi-Square Tests のところの
Linear-by-Linear Associationのところの values が 5.757 になっておりまして,一方,そのページのデータ 0 1 2 3 4+
Dropout 25 13 9 10 6 63
Remain 31 21 6 2 3 63
Total 56 34 15 12 9 126
を Cochran.Armitage 関数で分析した結果が> Cochran.Armitage(c(25,13,9,10,6), c(56,34,15,12,9))
カイ二乗値 自由度 P 値
トレンド 5.803028 1 0.01599860
直線からの乖離 3.655516 3 0.30114529
非一様性 9.458543 4 0.05060609
となり,Nがデータ総数を示す(今の場合126)なら,
5.803028 = 5.757 * 126 /125 = 5.803056
となるんですけどねぇ?
注:Cochran.Armitage は
http://aoki2.si.gunma-u.ac.jp/R/Cochran-Armitage.html
で定義しているものです
No.08795 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【尾島俊之】 2008/12/29(Mon) 10:14
青木繁伸先生
さっそく,レスポンスをありがとうございます。大夫解決しまして心より感謝致します。
そもそもの質問を言い換えますと,「世間で言われている,Mantel 検定や,Cochran-Armitage 検定の定義は何か。また,SPSSのサポートページに書かれている記述は正しいか」ということです。
青木先生に計算で確認して頂きましたので,SPSSのサポートページの記述:
> CA test statisitic = LLA * (N/(N-1))
は正しいのだろうと信じることにしたいと思います。
なお,そのサポートページのURLは,下記です。
http://support.spss.com/Tech/Troubleshooting/ressearchdetail.asp?ID=47847
(ただし,ログインしないと見られないかもしれません。)
ここで次なる疑問は,Linear-by-Linear Association と Mantel 検定とは,全く同一かということです。
これは,世間で言われているMantel 検定の定義は何かということ次第になるのでしょうね。
No.08796 I×2表(Iは順序尺度)の最も一般的な検定方法 【尾島俊之】 2008/12/29(Mon) 10:30
さらに,そもそもの質問がありました。
I×2表(Iは順序尺度)を検定する際に,最も一般的に推奨される方法は何か。
その名称は何か。
広く使われている統計ソフトを使って計算するにはどうしたらよいか。
ということになります。
それで,候補としては,
Cochran-Armitage test for trend
Mantel test (Mantel's trend test)
Linear-by-Linear Association
の3つが考えられます。
なお,International Epidemiological Association 2008 年発行の A dictionary of epidemiology には,
Mantel's trend test の項はありますが,Cochran-Armitage test for trend
や Linear-by-Linear Association の項はありませんでした。
Mantel's trend test の項には,簡単な説明のみで,残念ながら定義や文献は記載されていませんでした。
No.08797 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2008/12/29(Mon) 11:23
> Cochran-Armitage 検定の定義は何か
これは,相当に明らかでしょう。よく知られているといって良いと思いますよ。
Mantel 検定ってのは,どうなのか知りません。
> 正しいのだろうと信じることにしたいと思います。
疑うのもいいですけど,正しいかどうか,自分で検索なり計算なりで確かめればよいと思います。
> A dictionary of epidemiology には...ありませんでした
ないものを探してもしようがないし,その情報ソースが絶対的なものでもないでしょう。
> 広く使われている統計ソフトを使って計算するにはどうしたらよいか。
R の coin パッケージには Cochran-Armitage 検定を行う関数がありますね
### Cochran-Armitage test (permutation equivalent to correlation
### between dose and tumor), cf. Table 2 for results
independence_test(tumor ~ dose, data = lungtumor, teststat = "quad")
### linear-by-linear association test with scores 0, 1, 2
### is identical with Cochran-Armitage test
lungtumor$dose <- ordered(lungtumor$dose)
independence_test(tumor ~ dose, data = lungtumor, teststat = "quad",
scores = list(dose = c(0, 1, 2)))
"linear-by-linear
association test with scores 0, 1, 2 is identical with Cochran-Armitage
test" って,書いてありますね。Cochran-Armitage 検定では,独立変数は等間隔に限らず任意。Linear-by-Linear
は,それが等間隔の場合と。
No.08798 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2008/12/29(Mon) 13:08
No. 8729 で引用した記事をちゃんと読むと,いろいろ書いてありますよね。
M2 = (N - 1)r^2 というのが,Mantel's trend test の統計量だと書いてあります。r はピアソンの積率相関係数(カテゴリーに等間隔数値を与えたときの相関係数)> a <- rep(0:4, c(25,13,9,10,6))
> b <- rep(0:4, c(31,21,6,2,3))
> (r <- cor(rep(0:1, each=63), c(a, b))) # 相関係数
[1] -0.2146061
> n <- length(c(a, b))
> (chi2.MH <- (n-1)*r^2) # マンテル検定統計量
[1] 5.756972
そういえば,あそこに書いてあったかなと,SPSSのアルゴリズムマニュアルをみたら,確かにそう書いてありました。
Linear-by-Linear
は,You will see that the Linear-by-Linear Association measure = 5.757,
which is the same as the chi-square that we calculated using (N - 1)r^2
.
No.08809 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【尾島俊之】 2009/01/02(Fri) 10:05
青木先生
詳しい解説をありがとうございます。
だいぶ解きほぐされてきたような,でもちょっと引っかかります。
No. 8797
LLA と Cochran-Armitage test は identical (等間隔の場合)
No. 8798
LLA と マンテル検定統計量は same
No. 8795
CA test statisitic = LLA * (N/(N-1))
となって,No. 8797 と No. 8798 が矛盾します。
identical というのは一般的には,ぴったり同じということかなと
思いますが,N/(N-1)くらいの違いは認めて「だいたい同じ」という
意味に解釈すれば良いのかなと考えました。
用語がいろいろと出てきて,素人はとても混乱しますので,どこか,権威のある学会か何かで,コンセンサスを作っていただいて,用語が整理されて欲しいものだと思います。
しかし,統計学業界と疫学業界でコンセンサスが違ったりすると,また大変かなとも思いますが。
No.08810 I×2表(Iは順序尺度)の検定での間隔 【尾島俊之】 2009/01/02(Fri) 10:24
とりあえず困っていたことはだいたい解決できましのたで,ちょっと余談です。
No. 8797
"linear-by-linear association test with scores 0, 1, 2 is identical with Cochran-Armitage test"
ということは,Cochran-Armitage test では間隔は等間隔に固定で,LLA は間隔を自由に変えられる拡張版ということかなと理解しました。
では,間隔が不明な場合はどうでしょうか。
今,I×2表(Iは順序尺度)の検定について考えていますが,
2×I表の場合には,Wilcoxon's rank sum test を使えば良いのかなと思います。この場合,間隔は不明で構わないと理解しています。
(間隔が分かっていて正規分布の場合にはt検定)
以
前に,知り合いの統計学者の先生に伺ったところ,I×2表で間隔を気にしなくても良い方法は無いのではないか,もしくは累積カイ二乗検定を使ってお茶を濁
すかとのことでした。累積カイ2二乗検定を検索しましたところ,この掲示板の No.4356
が出てきまして,青木先生から「国際的にどの程度通用するか」との否定的なコメントがついていました。
やはり,I×2表で間隔が不明のものについて,ノンパラメトリックに検定するのは難しいのかなと思いました。
No.08811 普通の回帰とロジスティック回帰分析 【尾島俊之】 2009/01/02(Fri) 10:41
I×2表で,間隔がわかる場合についてに話しが戻りますが,No.4356 への青木先生のコメントを読み返して,もうひとつすっきりしていなかったことを思い出しました。
Cochran-Armitage test や LLA は普通の回帰分析の発想で作れれている手法だと思います。
一方で,アウトカムが2値ということから考えると,ロジスティック回帰分析の方が良いように思います。
I×2表の検定をしたい時に,普通の回帰と,ロジスティック回帰のどちらを使うかについて,理屈としてはどちらもそれぞれ正しいように思いますが,出し方が異なりますので,結果は微妙に異なります。
普通の回帰とロジスティック回帰分析のどちらの方がより良いでしょうか。
そもそも複数の検定方法がありえる場合に,どの方法がより良いかどうかは,何を基準に判断すれば良いのでしょうか。
モデルフィットの良さで決めるという方法もありえるでしょうが,観察された数字のちょっとした違いによって,最適な手法が変わったりするというのは,とても不安定で良くないような気もします。
No.08812 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2009/01/02(Fri) 11:27
> Cochran-Armitage test では間隔は等間隔に固定で,LLA は間隔を自由に変えられる拡張版ということかなと理解しました。
逆ですよ。
>>
"linear-by-linear association test with scores 0, 1, 2 is identical
with Cochran-Armitage test" って,書いてありますね。Cochran-Armitage
検定では,独立変数は等間隔に限らず任意。Linear-by-Linear は,それが等間隔の場合と。
> 用語がいろいろと出てきて,素人はとても混乱しますので,どこか,権威のある学会か何かで,コンセンサスを作っていただいて,用語が整理されて欲しいものだと思います。
しかし,統計学業界と疫学業界でコンセンサスが違ったりすると,また大変かなとも思いますが。
統計学業界と疫学業界って,,,変ですね。
疫学統計というのが独自にあるわけではなく,統計学の一部分が疫学における統計学でしょう。疫学統計で最善の方法は統計学においても最善の方法だと思いますけど。
「権威のある学会か何かで,コンセンサスを作っていただいて,用語が整理されて欲しいものだと思います」???
No.08813 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2009/01/02(Fri) 11:40
> 間隔が不明な場合はどうでしょうか。
そのような場合には,等間隔を仮定したり,もっと良い推定スコアとして平均順位スコアを使うのです(コクラン・アーミテージ検定の原論文を参照のこと)
> 2×I表の場合には,Wilcoxon's rank sum test を使えば良いのかなと思います
違うでしょうね。
コクラン・アーミテージ検定は,傾向検定 trend test です。
Wilcoxon's rank sum test は,位置母数の検定です。
> Cochran-Armitage test や LLA は普通の回帰分析の発想で作れれている手法
ロ
ジスティック回帰やプロビット回帰で回帰係数の検定をしても良いと思いますが,コクラン・アーミテージ検定は予測ではなくて,傾き(傾向)を対象にするの
で,それでよいと思いますけど。コクラン・アーミテージ検定は,一様性の検定統計量を線形傾向と,それからのずれに分解するものです。そういう点でも,両
者は目的が異なるということもあるでしょう。
No.08814 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2009/01/02(Fri) 12:10
すみません,以下は間違いでした。No. 8833 で,訂正します。
>> 2×I表の場合には,Wilcoxon's rank sum test を使えば良いのかなと思います
> 違うでしょうね。
反例は一つあれば十分。> d <- rbind(c(3,5,8,9,16), c(6,7,6,7,5))
> n <- colSums(d)
> plot(d[1,]/n, ylab="Proportion", ylim=c(0,1))
> Cochran.Armitage(d[1,], n)
カイ二乗値 自由度 P 値
トレンド 5.8768259 1 0.01534145
直線からの乖離 0.4880162 3 0.92151620
非一様性 6.3648421 4 0.17350814
> wilcox.test(d[1,], d[2,])
ウィルコクソンの順位和検定(連続性の補正)
データ: d[1, ] と d[2, ]
W = 15.5, P値 = 0.5982
対立仮説: location shiftは,0ではない
Warning message:
In wilcox.test.default(d[1, ], d[2, ]) :
タイがあるため,正確な p 値を計算することができません
ロジスティック回帰をやってみるといかのようになる。このデータの場合,上記トレンドに対するP値の方がやや小さいという結果になるが。> df <- data.frame(x=c(rep(1:5, d[1,]), rep(1:5, d[2,])),
+ g=rep(c("positive", "negaive"), c(41, 31)))
> ans <- glm(g~x, data=df, family=binomial)
> summary(ans)
Call:
glm(formula = g ~ x, family = binomial, data = df)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6205 -1.0963 0.7916 0.9489 1.5037
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.1757 0.6596 -1.783 0.0747 .
x 0.4351 0.1844 2.360 0.0183 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 98.42 on 71 degrees of freedom
Residual deviance: 92.44 on 70 degrees of freedom
AIC: 96.44
Number of Fisher Scoring iterations: 4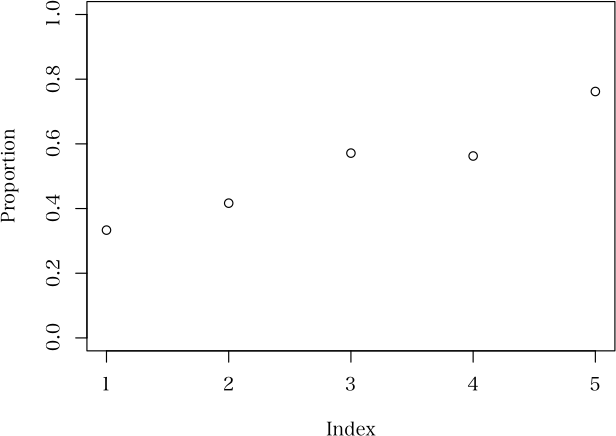
No.08815 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2009/01/02(Fri) 17:13
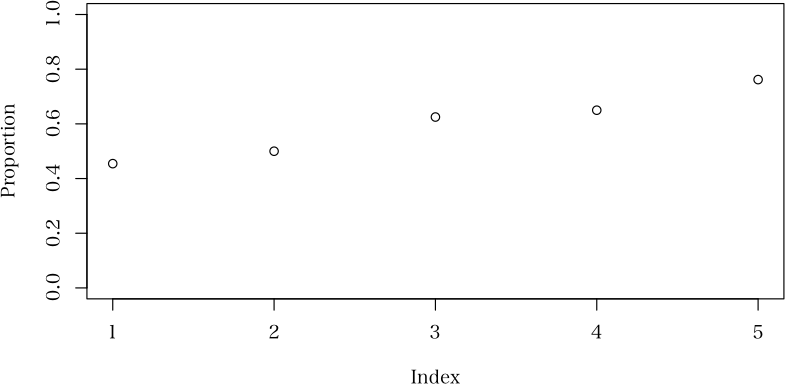
コクラン・アーミテージ検定では有意な傾向が見られるが,ロジットモデルの回帰係数は有意ではないという例> (d <- rbind(c(5,7,10,13,16), c(6,7,6,7,5)))
[,1] [,2] [,3] [,4] [,5]
[1,] 5 7 10 13 16
[2,] 6 7 6 7 5
> n <- colSums(d)
> plot(d[1,]/n, ylab="Proportion", ylim=c(0,1))
> Cochran.Armitage(d[1,], n)
カイ二乗値 自由度 P 値
トレンド 3.8706085 1 0.0491387
直線からの乖離 0.1429146 3 0.9862314
非一様性 4.0135231 4 0.4041788
> df <- data.frame(x=c(rep(1:5, d[1,]), rep(1:5, d[2,])),
+ g=rep(c("positive", "negaive"), rowSums(d)))
> ans <- glm(g~x, data=df, family=binomial)
> summary(ans)
Call:
glm(formula = g ~ x, family = binomial, data = df)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6568 -1.2130 0.7646 1.0068 1.2848
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.5814 0.5943 -0.978 0.3280
x 0.3323 0.1716 1.936 0.0528 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 108.75 on 81 degrees of freedom
Residual deviance: 104.86 on 80 degrees of freedom
AIC: 108.86
Number of Fisher Scoring iterations: 4
No.08816 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2009/01/02(Fri) 17:49
関数を作りました。色々なデータを与えて結果を比較すると良いでしょう。> Linear.by.Linear <- function(d)
+ {
+ n <- sum(d)
+ M <- (n-1)*cor(rep(row(d), d), rep(col(d), d))^2
+ CA <- M*n/(n-1)
+ return(list(Linear.by.Linear=c(M=M, p.value.M=pchisq(M, 1, lower.tail=FALSE)),
+ Cochran.Armitage=c(CA=CA, p.value.CA=pchisq(CA, 1, lower.tail=FALSE))))
+
+ }
> (d <- matrix(c(25,13,9,10,6, 31,21,6,2,3), byrow=TRUE, ncol=5))
[,1] [,2] [,3] [,4] [,5]
[1,] 25 13 9 10 6
[2,] 31 21 6 2 3
> Linear.by.Linear(d)
$Linear.by.Linear
M p.value.M
5.75697211 0.01642335
$Cochran.Armitage
CA p.value.CA
5.8030279 0.0159986
No.08819 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2009/01/03(Sat) 17:49
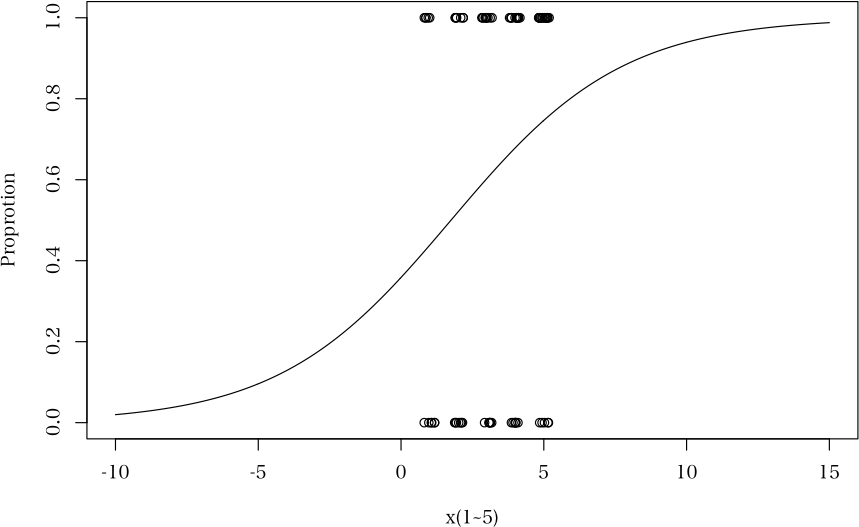
独立変数と従属変数の範囲にもよるのだけど,よほど極端な場合以外は,直線近似で十分な事が多いという例として。
先の例をロジスティック回帰したときの図を示しておきましょう。なお,データ点の重複があるので,実測値の横軸に jitter を加えてあります。(d <- rbind(c(5,7,10,13,16), c(6,7,6,7,5)))
n <- colSums(d)
plot(d[1,]/n, ylab="Proportion", ylim=c(0,1))
Cochran.Armitage(d[1,], n)
df <- data.frame(x=c(rep(1:5, d[1,]), rep(1:5, d[2,])), g=rep(1:0, rowSums(d)))
ans <- glm(g~x, data=df, family=binomial)
summary(ans)
df2 <- data.frame(x=seq(-10, 15, length=500))
x <- predict(ans, newdata=df2)
plot(df2$x, 1/(1+exp(-x)), type="l", ylim=c(0,1), xlab="x(1~5)", ylab="Proprotion")
points(jitter(df$x), as.integer(df$g))
No.08821 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【尾島俊之】 2009/01/03(Sat) 20:31
青木先生,大量のレスポンスありがとうございます。
>>
"linear-by-linear association test with scores 0, 1, 2 is identical
with Cochran-Armitage test" って,書いてありますね。Cochran-Armitage
検定では,独立変数は等間隔に限らず任意。Linear-by-Linear は,それが等間隔の場合と。
英文解釈で"with scores 0, 1, 2" の節がLLAを限定しているのだと思いましたが,Cochran-Armitage testに係っていたんですね。
>> 間隔が不明な場合はどうでしょうか。
> そのような場合には,等間隔を仮定したり,もっと良い推定スコアとして平均順位スコアを使うのです
そうですね。ありがとうございます。
>> 2×I表の場合には,Wilcoxon's rank sum test を使えば良いのかなと思います
> 違うでしょうね。
> コクラン・アーミテージ検定は,傾向検定 trend test です。
> Wilcoxon's rank sum test は,位置母数の検定です。
2×I表と,I×2表と,普通は言わない言い方で略しすぎました。
悪化,無効,やや有効,有効,著効
新薬 5, 7, 10, 13, 16
プラセボ 6, 7, 6, 7, 5
という問題の場合には,Wilcoxon's rank sum test
喘息
あり なし
農村周辺部 5 6
農村中心部 7 7
都市住宅地 10 6
都市商業地 13 7
都市幹線道 16 5
という問題の場合には,Cochran-Armitage test と理解していますが,いかがでしょうか。
No.08822 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2009/01/03(Sat) 21:11
一般的に,表側には原因,表頭には結果を置く方が良いとされているらしいことは了解しています。> 喘息
> あり なし
> 農村周辺部 5 6
> 農村中心部 7 7
> 都市住宅地 10 6
> 都市商業地 13 7
> 都市幹線道 16 5
> という問題の場合には,Cochran-Armitage test と理解していますが,いかがでしょうか。
農村周辺部 < 農村中心部 < 都市住宅部 < 都市商業地 < 都市幹線道
という意味ならばその通りでしょう。そのような場合には 農村周辺部 農村中心部 都市住宅部 都市商業地 都市幹線道
あり 5 7 10 13 16
割合% 45.5 50.0 62.5 65.0 76.2
なし 6 7 6 7 5
合計 11 14 16 20 21
の
ように書いた方がわかりやすいかもしれません。とはいっても,このような表示も,コクラン・アーミテージ検定の原著でそのように示していると言うだけと言
われればその通り。結局の所,どちらを表頭にしようが表側にしようが,意味を考えれば,正しい解釈(正しい検定法の選択)に行き着くと言うことでしょう。
No.08823 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2009/01/03(Sat) 22:19
> 英文解釈で"with scores 0, 1, 2" の節がLLAを限定しているのだと思いましたが,Cochran-Armitage testに係っていたんですね
失
礼しました。これについては,どっちもどっち。というか,私の思いこみが強すぎました。独立変数にどんな重み付けをしようが,CA=LL*N/(N-1)
になりますね。つまり,linear by linear
であろうとも,任意のスコア付けはできる(それが一般的かどうかは判定できませんが。少なくともコクラン・アーミテージ検定ではスコアが任意であることは
明示されている)。> x.i <- c(10, 20, 40, 80, 160) # 各群の外的基準変数の値
> n.i <- c(30, 35, 47, 21, 45) # 各群のケース数
> r.i <- c(2, 4, 14, 13, 39) # 各群の反応ケース数
>
> Cochran.Armitage(r.i, n.i, x.i)
カイ二乗値 自由度 P 値
トレンド 69.915406 1 6.190307e-17
直線からの乖離 2.671810 3 4.450392e-01
非一様性 72.587216 4 6.449422e-15
> Linear.by.Linear <- function(d)
+ {
+ n <- sum(d)
+ (n-1)*cor(rep(row(d), d), rep(2^(col(d)-1), d))^2
+
+ }
> d <- rbind(r.i, n.i-r.i)
> (ans <- Linear.by.Linear(d))
[1] 69.52262
> ans*sum(d)/(sum(d)-1)
[1] 69.9154
No.08833 Re: Mantel統計量とCochran-Armitage(CA)統計量の関係 【青木繁伸】 2009/01/06(Tue) 12:08
No. 8814 について,京都方面から指摘がありましたので,訂正します。
まず,wilcox.test の使用自体にミスがありました。> wilcox.test(rep(1:5, c(3, 5, 8, 9, 16)), rep(1:5, c(6, 7, 6, 7, 5)))
Wilcoxon rank sum test with continuity correction
data: rep(1:5, c(3, 5, 8, 9, 16)) and rep(1:5, c(6, 7, 6, 7, 5))
W = 843, p-value = 0.01575
alternative hypothesis: true location shift is not equal to 0
Warning message:
In wilcox.test.default(rep(1:5, c(3, 5, 8, 9, 16)), rep(1:5, c(6, :
タイがあるため,正確な p 値を計算することができません
で
した。したがって,ほぼ同じ結果を与えるということになり,Wilcoxon's rank sum test
でよいということになります。より正確な P 値を得るためには,exactRankTests パッケージの wilcox.exact
を使えば以下のようになります。> (ans2 <- wilcox.exact(rep(1:5, c(3, 5, 8, 9, 16)), rep(1:5, c(6, 7, 6, 7, 5))))
Exact Wilcoxon rank sum test
data: rep(1:5, c(3, 5, 8, 9, 16)) and rep(1:5, c(6, 7, 6, 7, 5))
W = 843, p-value = 0.01505
alternative hypothesis: true mu is not equal to 0
> ans2$p.value
[1] 0.01505210
さらに,No. 8823 で示したように,スコアはどんなものでもよいということで,平均順位(wilcoxon score)を用いる Mantel 検定(Linear-by-Linear 検定)をやってみることにします。まず,以下のような関数を定義します。wilcoxon.score <- function(n.i)
{
a <- cumsum(n.i)
a <- c(0, a[-length(a)])
return(a+(n.i+1)/2)
}
Mantel <- function(r.i, n.i, x.i)
{
if (length(x.i) == 1 && x.i == "wilcoxon") {
x.i <- wilcoxon.score(n.i)
}
n.r <- sum(r.i)
x <- rep(c(x.i, x.i), c(r.i, n.i-r.i))
y <- rep(1:2, c(n.r, sum(n.i)-n.r))
(sum(n.i)-1)*cor(x, y)^2
}
これを用いて,wilcoxon score を使う Mantel 検定の結果は以下のようになります。> r.i <- c(3, 5, 8, 9, 16)
> n.i <- c(9, 12, 14, 16, 21)
> ans <- Mantel(r.i, n.i, "wilcoxon")
> (p <- pchisq(ans, 1, lower.tail=FALSE))
[1] 0.01549875
こ
の P 値と,wilcox.exact の P 値は同じになるそうですが,ちょっと違いますね(どこかまだ,間違えている?)。ついでに,同じく
wilcoxon score を用いるコクラン・アーミテージ検定の結果は以下のようになり,この P 値も,いずれの P
値とも異なる(Mantel 検定の P 値と異なるのは当たり前ですが)> Cochran.Armitage(r.i, n.i, wilcoxon.score(n.i))
カイ二乗値 自由度 P 値
トレンド 5.9413884 1 0.01478936
直線からの乖離 0.4234537 3 0.93535602
非一様性 6.3648421 4 0.17350814
● 「統計学関連なんでもあり」の過去ログ--- 042 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る


