No.07495 Re: マン・ホイットニー検定の際の標本数の影響について 【青木繁伸】 2008/08/27(Wed) 22:09
二群に差があるとすればということで始めるか,差がない状況下で始めるかで結論は違うのではないかなと。
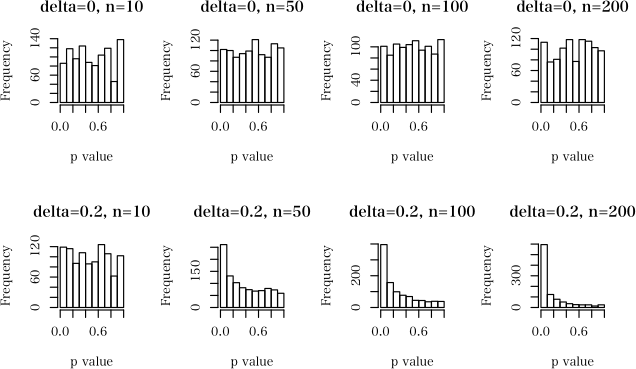
以下のようなシミュレーションをやってみましたけど。図の上の4つは位置母数に差がない場合。サンプルサイズをいくら多くしていってもP値は一様分布。
図の下の場合は,位置母数に差がある場合。サンプルサイズを大きくしていくとP値は小さくなる。要するにデータをたくさん集めれば有意だという結果が得られやすくなるということ。図をクリックすると原寸表示します
プログラムは以下のごとし(最適化していない)
sim <- function(n, delta=0, trial=1000)
{
result <- numeric(trial)
for (i in 1:trial) {
x1 <- rnorm(n)
x2 <- rnorm(n, mean=delta)
result[i] <- wilcox.test(x1, x2)$p.value
}
return(result)
}
layout(matrix(1:8, byrow=TRUE, ncol=4))
for (n in c(10, 50, 100, 200)) {
hist(sim(n, delta=0), main=paste("delta=0, n=", n, sep=""), xlab="p value")
}
for (n in c(10, 50, 100, 200)) {
hist(sim(n, delta=0.2), main=paste("delta=0.2, n=", n, sep=""), xlab="p value")
}
layout(1)