「統計学関連なんでもあり」の過去ログ--- 041

No.05502　プロビットモデル使用時の自然死・反復の扱い　　【虫】　2008/01/24(Thu) 01:46

プロビットモデルに関して質問いたします。虫の薬剤に対する感受性を調べる実験を行い，LD50値を求めるためプロビットモデルを使用したいと考えました。
質問1）対照区（薬剤を処理しなかった実験区）で死亡が認められたため，Abbottの式を用いて薬剤処理区の死亡率を補正したのですが，その後の計算において死亡個体数として観測値を使用しても良いのでしょうか。死亡個体数も補正してあげる必要はないでしょうか。例えば，対照区で10個体中1個体が死亡し，ある薬量の処理区で10個体中5個体が死亡したならば，その処理区での死亡個体数は補正をかけて「4.4」という数値を用いる必要はないでしょうか。
質問2）各試験区において反復を設けた場合，供試個体数，死亡個体数および死亡率については反復間の平均値をLD50値を求めるために用いても良いのでしょうか。あるいは反復での合計値を用いるべきなのでしょうか。例を挙げるならば，反復1～3について(供試験個体数, 死亡個体数, 死亡率)がそれぞれ(10, 4, 0.4) (11, 5, 0.45)　(11, 3, 0.27)　だった場合に，平均値(10.7，4, 0.37)と合計値(32, 12, 0.37)のいずれを用いるのが正しいのでしょうか。
ご教授の程，よろしくお願い申し上げます。

No.05506　Re: プロビットモデル使用時の自然死・反復の扱い　　【青木繁伸】　2008/01/24(Thu) 09:12

用量-反応関数にアボットの補正モデルを使うんじゃなかったかなあ？
死亡率 = p0 + (1-p0) * f(dose)
p0 が自然死亡率，f が今の場合プロビット関数 1/(1+Prob(g(dose)))
p0 と g() の係数をともに推定する

古いページに載せてあった
http://aoki2.si.gunma-u.ac.jp/RiskAssessment/background.html
役に立つかどうか分かりませんが

No.05507　Re: プロビットモデル使用時の自然死・反復の扱い　　【青木繁伸】　2008/01/24(Thu) 09:17

2）について
反復が全く同一条件（施設，時期，飼育方法等々）で行われたのならばプールして良いでしょうが，そうでない場合は，プールしない方がよいでしょう。

No.05508　Re: プロビットモデル使用時の自然死・反復の扱い　　【知ったかぶり】　2008/01/24(Thu) 10:38

ここで言うAbbottの式は，
補正死亡率＝（対照区の生存率ー処理区の生存率）/対照区の生存率
フツーは，補正死亡率からプロビット法によりLD50値を求める．反復がある場合は，処理区毎に補正死亡率の平均値を算出しちゃうのが一般的だと思います（虫関係では）．

たぶん，そんなやり方でよいのか？ということで，生存数，死亡数の生データに対し，プロビットモデルをあてはめることを考えておられるのだと思います．その場合，反復はプールしないほうがよいでしょうが，死亡個体数の補正をどうするか？補正しないと容量0の時に死亡率が0とならないことになってしまいますよね．LD50の値には影響しないような気もしますが．．．

解答になっていなくてごめんなさい．

No.05511　Re: プロビットモデル使用時の自然死・反復の扱い　　【青木繁伸】　2008/01/24(Thu) 13:32

私の書いたアボットの式とは違ったようですが，以下のような例を挙げて説明（Rを使います）

テストデータ
> data.frame(x, n, r, y)
  x  n  r         y
1 0 19  4 0.2105263
2 1 20  5 0.2500000
3 2 20  6 0.3000000
4 3 18 12 0.6666667
5 4 20 18 0.9000000
6 5 20 19 0.9500000
自然死亡率は 0.2 程度かなということですが，これもデータから推定します。
推定式は，
ロジスティック：y = p0+(1-p0)*(1/(1+exp(-a-bx)))
または
プロビット：y = p0+(1-p0)*(pnorm(a+bx))
y: 死亡率（=r/n），p0: 自然死亡率，a, b パラメータ
実行例（プロビットモデル）
> fun <- function(p, model=c("probit", "logistic"))
+ {
+ 	if (model == "logistic")
+  	y2 <- p[1]+(1-p[1])*(1/(1+exp(-p[2]-p[3]*x)))
+  	else
+ 	y2 <- p[1]+(1-p[1])*(pnorm(p[2]+p[3]*x))
+ 	return(sum((y-y2)^2))
+ }
> p <- c(0, 1, 1)
> x <- 0:5
> n <- c(19, 20, 20, 18, 20, 20)
> r <- c(4, 5, 6, 12, 18, 19)
> y <- r/n
> ans <- optim(p, fun, model="probit")
> plot(x, y, pch=19, ylim=0:1, xlim=c(0, 6))
> x2 <- seq(0, 6, length=300)
> p <- ans$par
> # y2 <- p[1]+(1-p[1])*(1/(1+exp(-p[2]-p[3]*x2)))
> y2 <- p[1]+(1-p[1])*(pnorm(p[2]+p[3]*x2))
> lines(x2, y2)
> abline(h=c(0.2, 1), lty=3)
> ans
$par
[1]  0.2169567 -3.3863066  1.1628000

$value
[1] 0.004477226

$counts
function gradient 
     210       NA 

$convergence
[1] 0

$message
NULL
結果的に，自然死亡率は 0.217 程度と推定
あてはめ図は以下の通り（クリックすると原寸表示）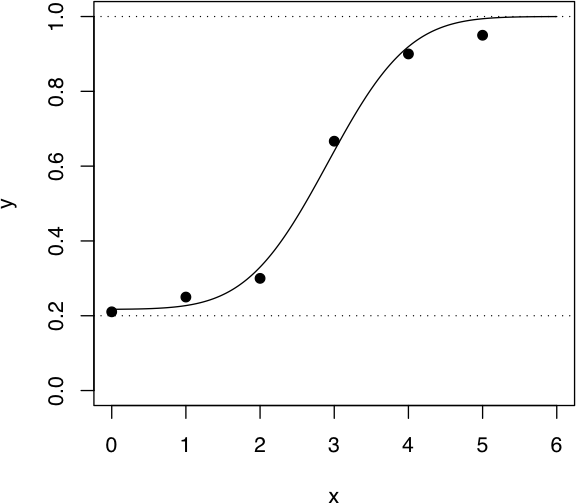

No.05519　Re: プロビットモデル使用時の自然死・反復の扱い　　【虫】　2008/01/24(Thu) 23:00

知ったかぶり様
補足いただきありがとうございます。いわんとしていることはまさにご指摘の通りです。

青木先生
質問1につきましては，ご指摘の補正モデルをもとにもう少し考えてみることとします。自然死亡率も推定値になる，という点は全く考えていませんでした(無処理区の実測値から得られた死亡率をそのまま自然死亡率として何の疑問も持っていませんでした）。また，Rのプログラムまでつけていただき有難う御座います。
質問2について重ねて質問いたします。
先生は状況によるだろうとの回答，知ったかぶりさんは私の質問の意図を察するに反復はプールしないほうがよさそうという回答でした。
もし反復をプールしないならば，反復の数だけLD50値がでてきてしまうと理解しますが，その場合，厳密性を要求しない場面では「結局どの数値を採用したらいいの？」と混乱を招くように思われます。加えて，私の例のようなケースで反復をとるのは，反復間でデータのばらつきがなさそうだということを確認するためだと思っております（ガラス瓶あたりの個体数に限りがあるとの実験操作上の理由もあります）。したがって，反復間でデータのばらつきがないことを確認→ 反復をプールしてLD50値を算出という手順ではどうかと考えるのですが，どうでしょうか？またその場合，反復間でデータのばらつきがない，あるいはその濃度における死亡率から考えていずれの反復の観測値も妥当である，ということを検定することは出来ますでしょうか？
以上，ご教授の程よろしくお願い申し上げます。

No.05520　Re: プロビットモデル使用時の自然死・反復の扱い　　【青木繁伸】　2008/01/24(Thu) 23:28

> もし反復をプールしないならば，反復の数だけLD50値がでてきてしまうと理解しますが

なぜソウなのですか？先に示した例だと，同じxに対して複数の実験結果があるというだけでしょう。データ点が増えるだけです
> cbind(x, n, r, y)
      x  n  r         y
 [1,] 0 19  4 0.2105263
 [2,] 0 20  3 0.1500000
 [3,] 1 20  5 0.2500000
 [4,] 1 21  4 0.1904762
 [5,] 1 18  5 0.2777778
 [6,] 2 20  6 0.3000000
 [7,] 2 20  7 0.3500000
 [8,] 3 18 12 0.6666667
 [9,] 3 20 14 0.7000000
[10,] 3 20 13 0.6500000
[11,] 4 20 18 0.9000000
[12,] 4 18 15 0.8333333
[13,] 5 20 19 0.9500000
などなど
分析すると以下のような感じ
> ans <- optim(p, fun, model="probit")
> plot(x, y, pch=19, ylim=0:1, xlim=c(0, 6))
> x2 <- seq(0, 6, length=300)
> p <- ans$par
> # y2 <- p[1]+(1-p[1])*(1/(1+exp(-p[2]-p[3]*x2)))
> y2 <- p[1]+(1-p[1])*(pnorm(p[2]+p[3]*x2))
> lines(x2, y2)
> abline(h=c(0.2, 1), lty=3)
> ans
$par
[1]  0.1859215 -2.6558754  0.9405136

$value
[1] 0.01910176

$counts
function gradient 
     346       NA 

$convergence
[1] 0

$message
NULL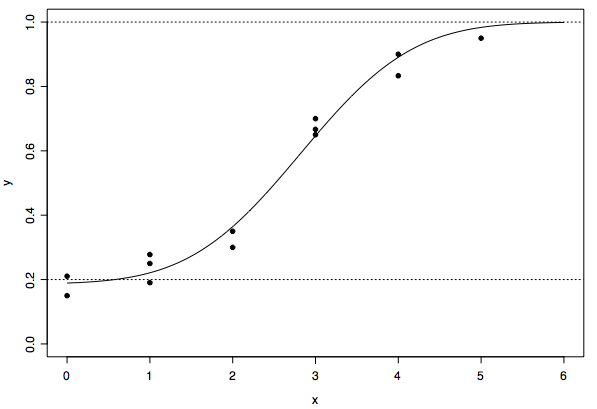

No.05554　Re: プロビットモデル使用時の自然死・反復の扱い　　【知ったかぶり】　2008/01/27(Sun) 17:07

便乗質問です．

青木先生のデータ（No.5520）をMASSライブラリーのdose.p()で分析すると，
> x <- c(0,0,1,1,1,2,2,3,3,3,4,4,5)
> n <- c(19,20,20,21,18,20,20,18,20,20,20,18,20)
> r <- c(4,3,5,4,5,6,7,12,14,13,18,15,19)
> dt <- cbind(dead = r, alive = n - r)
> pm <- glm(dt ~ x, family = binomial(probit))
> dose.p(pm, cf = 1:2, p = 0.5)
p = 0.5: 2.235554 0.1628136　 # LD50，SE
これは，青木先生のプログラムED50の結果と一致します．
http://aoki2.si.gunma-u.ac.jp/R/ed50.html

一方，No.5520で推定されたパラメータからLD50を求めると，
> (qnorm(0.5) - ans$par[2]) / ans$par[3]　＃容量－反応関数から算出
[1] 2.823857
かなり異なります．glm()の結果をプロットしてみると，明らかにoptim()による推定結果の方があてはまりが良い．これは，パラメータとして自然死亡率が含まれているか否かの違いだと思いますが，自然死亡率が高い場合は，glm()およびdose.p()によるLD50の推定は避けた方が良いという解釈でよろしいでしょうか．

No.05555　Re: プロビットモデル使用時の自然死・反復の扱い　　【青木繁伸】　2008/01/27(Sun) 17:22

自然死亡率が高かろうと低かろうと，自然死亡率をパラメータにした方が宛はまりはよいのはあきらかです。あえて自然死亡率を無視するモデルを立てる必要性があるならともかく。

発ガン試験の解析においては常に自然発ガン率を考慮するモデルを採用していましたね。

No.05561　Re: プロビットモデル使用時の自然死・反復の扱い　　【知ったかぶり】　2008/01/28(Mon) 11:27

ご返答ありがとうございます．
optim()による最適化というのが実のところよくわからない（初期値の取り方とか）ので，勉強してみます．