「統計学関連なんでもあり」の過去ログ--- 041

No.05425　r個の箱にn個のボールを入れたとき、ひとはこにｚ個以上入る確率は？　　【さんてららぽん】　2008/01/17(Thu) 22:35

期待値を求めたいと思っています。
r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？
ただし，1<=r<=50 0<=n<=50 Z=2 or 3 です。
たとえば，10個の箱のなかに，ボールを50個おとして，ひとつの箱に2個入っている期待値は？（3個入っている期待値は？）というわけです。
いくつかの数字で試してみたいので，公式が出来るとありがたいです。
あまりにも昔に習ったことなので，忘れてしまいました。
よろしくお願いいたします。

No.05426　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【青木繁伸】　2008/01/17(Thu) 22:50

> ひと箱にz個以上
どの箱に入れるかは無作為ということなんでしょうね？

No.05427　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【さんてららぽん】　2008/01/17(Thu) 23:22

はい，どの箱に入るかはわかりません。
本当のことを言うと，ひとつの箱からひもを巻きだしていて，そのひもが無作為に切れる。
10個の箱から巻きだして，合計で50回切れたとします。（実際は，同時に使用しているので，どの箱で切れたのかわからない。ただ，切れた回数だけは記録に残っている。）1箱につき2回以上切れる期待値，（3回以上も）を求めたい。
いつ，どこで，どの頻度で切れるかはわかりません。
ボールにたとえたほうがわかりやすいかなとおもって書きました。

No.05428　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【青木繁伸】　2008/01/17(Thu) 23:29

たとえ話は，ますますわかりにくい。。。（たとえ話が，百害あって一利なしであることの実例は，この掲示板には「五万とある」）
たとえ話が具体的なら，シミュレーションすれば，どのような分布に従うのかは，逆にはっきりする。
データの生成機序や，データの処理方法などのアルゴリズムは，言葉で述べるのは非常に曖昧。プログラムにすれば明快。明快なプログラムにより生成されたデータがどのような分布に従うかどうかは明らかに判定できる。
データの生成機序だけを見れば分かる場合もあるし，生成されたデータについて分析してみて初めて（本当は理論的に考えれば分かるにしても）分かることもあろう。
No.5425 で与えられて条件だけで，そのデータの分布が何であるか分かれば，ああだこうだ言う必要はないのであろう。

No.05438　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【さんてららぽん】　2008/01/18(Fri) 13:51

ご指導ありがとうございます。より具体的に書きます。
10箱まとめて購入したひもが，途中でぶちぶちと切れます。
10箱使用している間に6回切れました。
どの箱で切れたのかは今となってはわかりません。
（一箱につき，どのくらい切れるかを記録しておけばよかったのですが，もうわからなくなってしまいました。）

今後，ひとつの箱で，2回（または）3回以上切れた場合，
一度その箱は，使用禁止にしていこうと思います。
それは，その箱はおそらく切れやすい箱だろうと，今までの経験で考えるからです。

使用禁止にすると，その分，多めに注文しておかないと在庫切れになります。
ということで，どのくらい多めに注文すべきかということで，期待値を出したいなと思いました。

わかっていただけましたでしょうか？

No.05439　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【青木繁伸】　2008/01/18(Fri) 15:37

ポアソン定数＝0.6（一箱あたり切れる確率）のポアソン分布ではないでしょうか
xは一箱の糸が切れる回数，pはそのようなことが発生する確率（2回切れるのが9.879%など），Pはそれ以上のことが発生する確率（2回以上切れる確率は12.19%など）
> x <- 0:7
> round(data.frame(x=x, p=dpois(x, 0.6), P=ppois(x-1, 0.6, lower.tail=FALSE)), 5)
  x       p       P
1 0 0.54881 1.00000
2 1 0.32929 0.45119
3 2 0.09879 0.12190
4 3 0.01976 0.02312
5 4 0.00296 0.00336
6 5 0.00036 0.00039
7 6 0.00004 0.00004
8 7 0.00000 0.00000

No.05449　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【さんてららぽん】　2008/01/19(Sat) 09:18

お返事ありがとうございます。
0.6と決めてしまうところに戸惑いがあったのですが，そこを定数にするという考えなのですね。このシュミレーションをより確からしいものにするためには，もっとサンプルサイズを増やしていけばよいかなと思ってます。
よくある話ですが，製品ロットの間ではばらつきがあるので，その差も見てみようと思います。

No.05450　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【さんてららぽん】　2008/01/19(Sat) 09:29

再びすみません。
自分で計算してみようとおもって，先生のHPからポアソン分布についてみてみたのですが，上記のようなプログラムは，どのページから使えますか？0.6以外の数字（0．7や0．8）でもためしてみて，最悪のことを想定して，注文数を決めたいと思っています。

No.05451　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【青木繁伸】　2008/01/19(Sat) 11:34

> どのページから使えますか

R のコンソールに以下のように入力するだけですよ
pを変えるということなので一行目の数値を変えればよいようにしました。

p <- 0.6
x <- 0:7
round(data.frame(x=x, p=dpois(x, p), P=ppois(x-1, p, lower.tail=FALSE)), 5)

No.05497　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【さんてららぽん】　2008/01/23(Wed) 21:18

たびたびすみません。
下記，リンクを使っていたのですが，このことをおしゃっていますか？
もし，違ったら，web addressを教えていただけませんか？初心者ですみません。
　

No.05498　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【青木繁伸】　2008/01/23(Wed) 21:23

> 下記，リンクを使っていたのですが，このことをおしゃっていますか？
> もし，違ったら，web addressを教えていただけませんか？初心者ですみません。

なんのことか，さっぱり分かりませんが？

No.05499　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【さんてららぽん】　2008/01/23(Wed) 22:21

R のコンソールに以下のように入力するだけですよ
pを変えるということなので一行目の数値を変えればよいようにしました。

p <- 0.6
x <- 0:7
round(data.frame(x=x, p=dpois(x, p), P=ppois(x-1, p, lower.tail=FALSE)), 5)

とお返事をいただいたのですが，私が試そうと思っていたサイトは，先生のHPの中にある，ここにリンクしてあるサイトです。
たぶん，なにかプログラムで計算しているように見えるのですが，Rのコンソールということが理解できません。（HPで調べてみたのですが，わかりませんでした。）

No.05500　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【青木繁伸】　2008/01/23(Wed) 23:26

失礼しました。R がなにか分からないと，というか，R を知らなければ，No. 5451 のようなものを見せられても分かるわけがないですよね。

しかし，昔習ったけど忘れたということでしたので，ポアソン分布であるという回答で十分かと思ってしまいました。ポアソン分布であるということで，Excel を使うなりすれば計算はできると思ったのです。

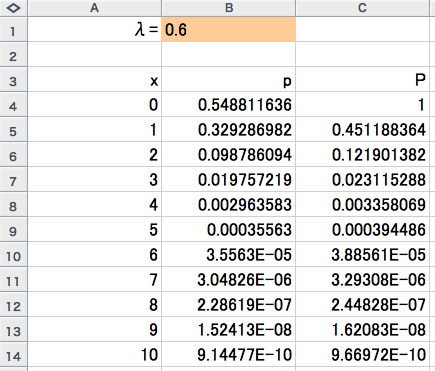
Excel のワークシートを作ったので，以下に示すリンクをクリックすればダウンロードできます。B1のセルにポアソン定数を入力すると計算します。

http://aoki2.si.gunma-u.ac.jp/lecture/mb-arc/poisson.xls

No.05521　Re: r個の箱にn個のボールを入れたとき，ひとはこにz個以上入る確率は？　　【さんてららぽん】　2008/01/24(Thu) 23:45

ありがとうございました。これで解決しました。どういうバッチの製品を購入したとしても，計算できます。
製品の不良率　ということに関しては，常に戦っていかないといけないので，時間を見つけてもう少し統計を学んでいければと感じました。
初心者への対応，どうもありがとうございました。